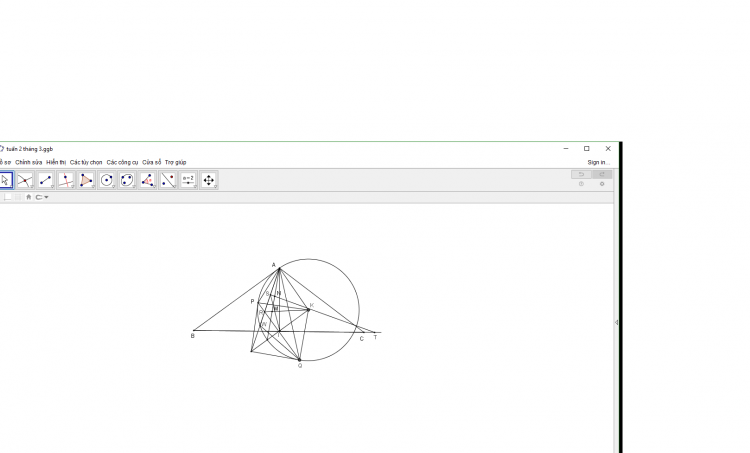
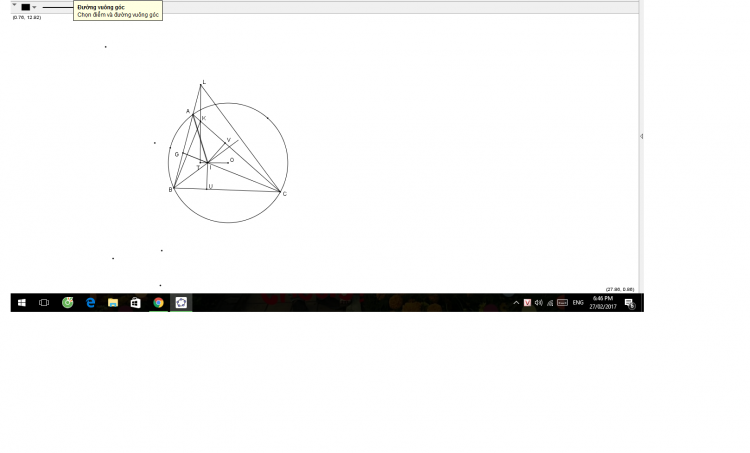
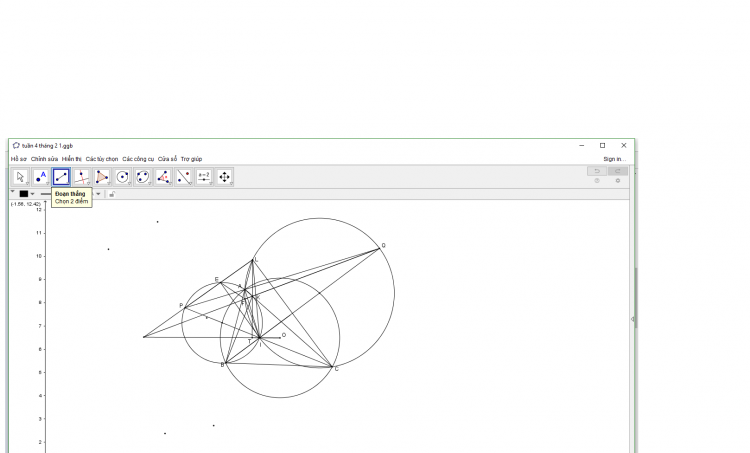
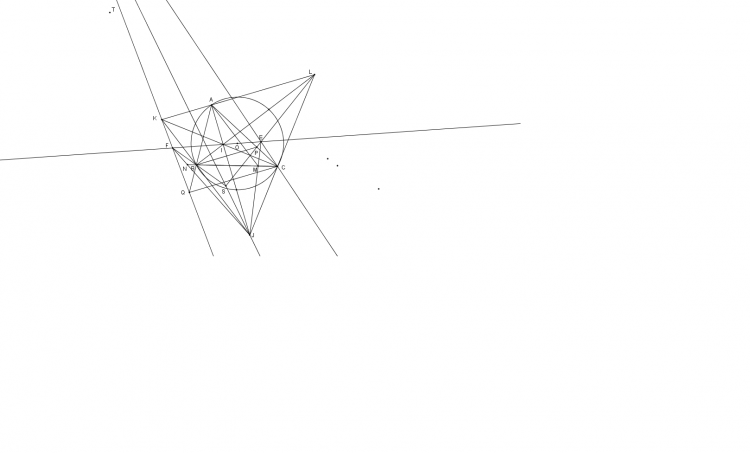
ta chứng minh bổ đề sau
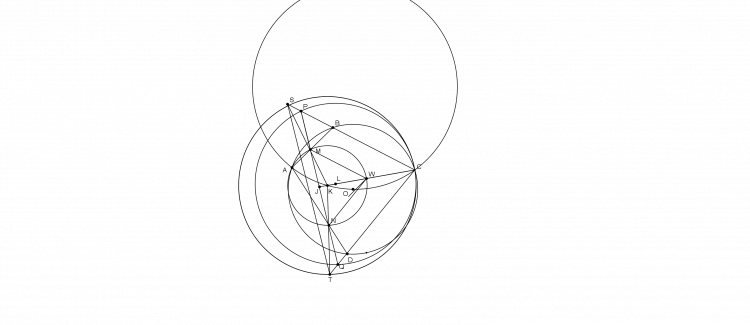
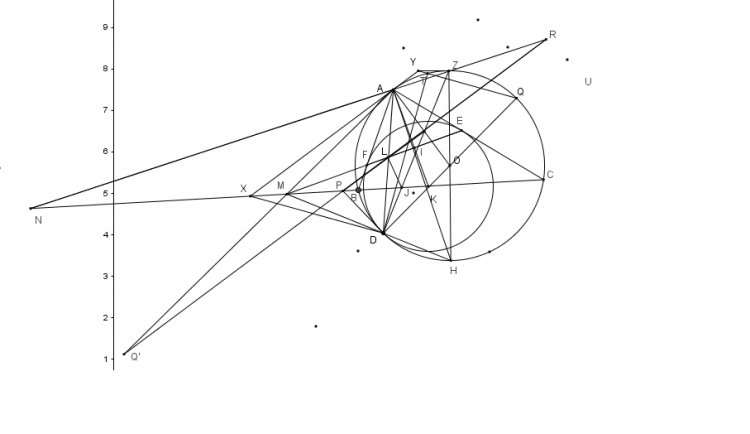
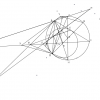
Cho tứ giác ABCD nội tiếp (O) ,K thuộc (AOC), đường tròn (K,KA) cắt AB,AD tại M,N,đường tròn (K,KC) cắt CB,CD tại S,T chứng minh MN//ST
cho AC cắt (K,KA),(K,KC),OK tại Q,V,X.$AO\cap AO=Y$
có $\widehat{KVC}=\widehat{KCA}=\widehat{KOA}$ $\Rightarrow$ XVOYnội tiếp
ta có $\widehat{OKC}=\widehat{XCO}$ $\Rightarrow$ $\widehat{KXC}$=$\widehat{KCO}$=$\widehat{KAY}$=$\widehat{KYA}$
$\Rightarrow Y\in (K,KA)$
C/M tt QK$\cap$ OC= H $\Rightarrow$ H$\in$ (K,KC)
Ta có (AB,AC)=(AM,AQ)$\Rightarrow$ (KM,KQ)$\Rightarrow$ (OB,OC) Gọi MK$\cap$ OB=Z$\Rightarrow$ (ZK,ZO)=(HK,HO)$\Rightarrow$ HKOZnội tiếp $\Rightarrow \widehat{KZO}=\widehat{KHO}=\widehat{KCO}=\widehat{OYK}$ $\Rightarrow$ KOYHZ nội tiếp
$\Rightarrow$(KOY)$\cap$ OB=Z
Tương tự (CB,CA)=(CS,CV)$\Rightarrow$ (OB,OA)=(KS,KV). SK$\cap OB=Z'$
dễ dàng chứng minh Z'$\in$ (HKY)$\Rightarrow$ (KOY)$\cap$ OB=Z'$\Rightarrow$ Z$\equiv $Z'$\Rightarrow$ $\overline{S,M,K}$
C/m tt $\overline{K,N,T}$
$\Rightarrow$ MN//ST $\Rightarrow PQ//ST$
$\Rightarrow$ $\overline{L,K,C}$
KC$\cap$ (K,KA)=W $\Rightarrow$ NW//TC và MW//SC
$\Rightarrow$ $\frac{JN}{NQ}$=$\frac{JW}{WC}$=$\frac{JM}{MP}$ $\Rightarrow$ $\frac{MP}{NQ}$=$\frac{JM}{JN}$
- Zaraki, Bonjour, ecchi123 và 2 người khác yêu thích

 Tìm kiếm
Tìm kiếm Nữ
Nữ












 Gửi bởi
Gửi bởi