Nerus

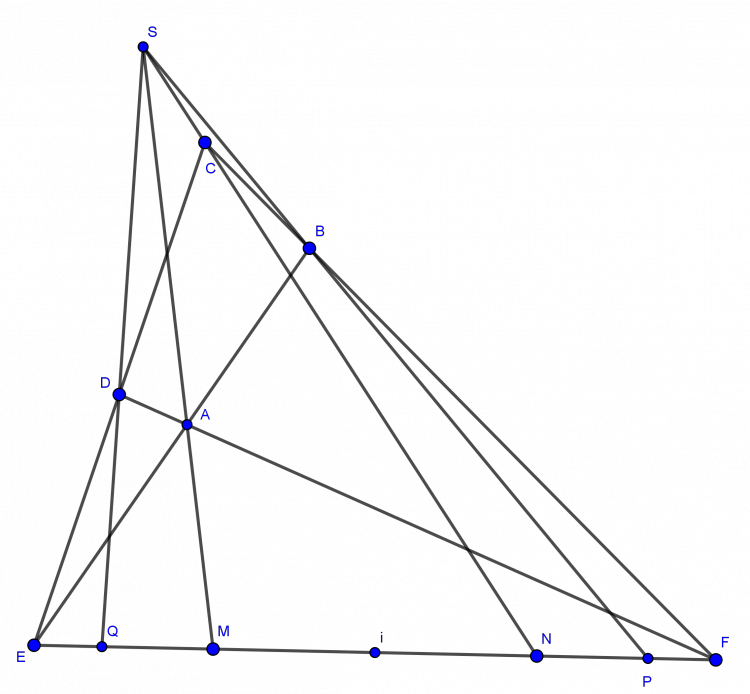
Theo $Pascal$, có $\overline{H,I,A}$

Dễ thấy vị tự tâm $H$ tỉ số $\frac{HI}{HA}$ thì $\left ( S \right ) \mapsto \left ( O \right )$ nên $\overline{H,O',A'}$.

Do $IO'\parallel AA'$  ( $EF$ là đối song ) nên theo $Talet$ có đpcm

[BÀI 2]

Áp dụng đl Menelaus

Trong $\Delta SNP$ có $\overline{C,B,F}$ nên $\frac{\overline{FP}}{\overline{FN}}.\frac{\overline{CN}}{\overline{CS}}.\frac{\overline{BS}}{\overline{BP}}=1$        [1]

Trong $\Delta SNQ$ có $\overline{C,D,E}$ nên $\frac{\overline{EQ}}{\overline{EN}}.\frac{\overline{CN}}{\overline{CS}}.\frac{\overline{DS}}{\overline{DQ}}=1$      [2]

Trong $\Delta SMP$ có $\overline{E,A,B}$ nên $\frac{\overline{EM}}{\overline{EP}}.\frac{\overline{BP}}{\overline{BS}}.\frac{\overline{AS}}{\overline{AM}}=1$       [3]

Trong $\Delta SMQ$ có $\overline{F,A,D}$ nên $\frac{\overline{FM}}{\overline{FQ}}.\frac{\overline{DQ}}{\overline{DS}}.\frac{\overline{AS}}{\overline{AM}}=1$      [4]  

Lấy [2] : [1] x [4] ; [3] ta có

$\frac{\overline{EQ}}{\overline{EN}}.\frac{\overline{FN}}{\overline{FP}}=\frac{\overline{EM}}{\overline{EP}}.\frac{\overline{FQ}}{\overline{FM}} \Rightarrow \frac{\overline{QE}}{\overline{QF}}= \frac{\overline{PF}}{\overline{PE}}$ do  $\overline{EN}=-\overline{FM},\overline{EM}=-\overline{FN}$

Từ đó có đpcm

Bài 2,

Gọi $EF$ cắt $BC$ tại $S$. $SK$,$AR$ cắt $\left ( K \right )$ tại $P,Q,U,V$, Do $AR\perp SK$ nên $P,Q$ là 2 điểm chính giữa cung $UV$ Theo bổ đề quen thuộc ta có $\overline{M,R,Q},\overline{N,R,P}$

Từ A kẻ tiếp tuyến $AG$,$AH$ đến $\left ( K \right )$ thì $\overline{S,R,G,H}$ . Dễ có -1 = $ ( S,R,G,H )$ = $ Q( S,R,G,H )$ = $ ( P,M,G,H )$ nên $ GMHP$ điều hòa từ đó có  $\overline{M,A,P}$

Tương tự $\overline{N,A,Q}$.

Từ đó bằng chiếu xuyên tâm ta có $\overline{M,N,S}$

Suy ra $MN,EF,BC$ đồng quy, Gọi $ME$ cắt $NF$ tại $L$. Có $S$ và $L$ liên hợp với nhau qua $\left ( K \right )$ mà $AR$ là đối cực của $S$ qua $\left ( K \right )$ nên có đpcm

Bài 2;

Có $\Delta IDB = \Delta IEC$ nên $IE=ID=IF$ do đó $\Delta FDE$ vuông tại $D$

lại có $\angle IDB$ =  $\angle IEC$ nên $IDBE$ nội tiếp suy ra $\angle IBD$ = $\angle IED$

nên $\angle FDI$ = $\angle DFI$ = $90^{0}$ - $\angle DEF$ = $90^{0}$- $\angle DBI$ = $\angle BDH$

suy ra $\angle FDH$ = $\angle IDB$ = $\angle FEC$

Mặt khác có $\Delta BDH\sim \Delta EFD$  nên $\frac{EF}{FD}= \frac{BD}{DH}= \frac{EC}{DH}$ nên $\Delta FDH\sim \Delta FEC$ suy ra $\Delta FDE\sim \Delta FHC$ nên $\angle FHC$ = $90^{0}$

cho AB,AC là 2 tiếp tuyến của (O)(B,C là tiếp điểm). Gọi E,F là trung điểm AB,AC.Từ M nằm giữa E và F kẻ tiếp tuyến MT với (O)(T là tiếp điểm),MT cắt AB,AC tại P,Q.Chứng minh rằng: MA=MT

P,Q để làm gì thế bạn?

Gọi MA cắt BC,(O) tại X,Y,Z suy ra $MA^{2}$=$MX^{2}$=MZ.MY=$MT^{2}$ suy ra đpcm

Bạn có thể biến đổi tương đương

dpcm $\Leftrightarrow \sum \left ( \frac{1}{a^{2}}-a^{2} \right )\geq 0\Leftrightarrow \sum \left ( \frac{1}{a}-a \right )\left ( \frac{1}{a}+a\right )\geq 0$

Áp dụng bđt Cosi ta sẽ CM $2\sum \left ( \frac{1}{a}-a \right )\geq 0\Leftrightarrow \sum \frac{1}{a}-3\geq 0\Leftrightarrow \sum \frac{1}{a}\geq \frac{9}{\sum a}$ ( đúng ) 

có thể tham khảo thêm trong đây nữa

Bài 4

a,Gọi giao điểm của đường tròn qua A,B tiếp xúc với AC cắt đường tròn qua A,C tiếp xúc với AB tại X

Có $\Delta BXA\sim \Delta AXC$ và $\frac{QA}{QC}= \frac{PB}{PC}= \frac{RB}{RC}$

nên $\Delta BXR\sim \Delta AXQ$ do đó $\widehat{RXQ}= \widehat{AXB}= 180^{0}-\widehat{RAQ}$ suy ra AQXR nội tiếp

b, Gọi tiếp tuyến tại B,C của O giao nhau tại S, dễ có X thuộc $\left ( BSC \right )$, lấy AS cắt BC tại T 

do $\left ( AKTS \right )= -1$ và TX.TS=TB.TC=TA.TK nên X là trung điểm AK

Cho tam giác ABC nội tiếp (O), trực tâm H. I là trung điểm AH. Đường thẳng qua I vuông góc với OI cắt (O) tại M,N. Gọi H' là trực tâm tam giác CMN. Chứng minh B,H,H' thẳng hàng 

Cho tam giác ABC nội tiếp (O). Đường cao AD,BE,CF đồng quy tại H. EF và (AEF) cắt (O) tại M,N và G. Chứng minh GM,NH,BC đồng quy

Gọi $G'$ là trung điểm $HK$. $AH$ cắt $BC$ tại $F$. Gọi $I,J$ là trung điểm $AH,MH$

qua phép vị tự tâm $H$ tỉ số $\frac{1}{2}$ suy ra $G'$,$I$,$J$ thuộc $\left ( DEF \right )$. Ta có $HA.HF=2.HI.HF=2HJ.HG'=HM.HG$ nên $AMFG'$ nội tiếp 

Mặt khác có $\Delta AME\sim \Delta ABM$ nên $AM^{2}=AE.AB=AH.AF$ suy ra $\Delta AHM\sim \Delta AMF$ nên $\widehat{AMH}=\widehat{AFM}$ hay $A$ là điểm chính giữa cung $MG'$ suy ra $AG'=AM=AN$ và do $KA$ là phân giác $MKN$ nên $NG'$ là trung trực $AK$ nên $G'$ trùng $G$ hay $G$ là trung điểm $HK$

$HP$ cắt $O$ tại $Q$ thì $P$ là trung điểm $HQ$ suy ra $PG$ ll $KQ$ ll $NG$ nên có đpcm

Cho $\Delta ABC$ nội tiếp $\left ( O \right )$. $A$ di chuyển trên cung lớn $BC$. Vẽ $\left ( W_{1} \right )$ qua $A,B$ tiếp xúc với $AC$. Tương tự có $\left ( W_{2} \right )$. $\left ( W_{1} \right )$ cắt $\left ( W_{2} \right )$ tại $G$. $CG.BG$ cắt $\left ( W_{1} \right ),\left ( W_{2} \right )$ tại $P,Q$. $QA,PA$ cắt $\left ( W_{1} \right )$ cắt $\left ( W_{2} \right )$ tại $K,L$. $KB$ cắt $LC$ tại $S$. $AS$ cắt trung trực $BC$ tại $T$. Gọi $J$ là tâm $\left ( TPQ \right )$. CMR $JS$ đi qua điểm cố định khi $A$ di chuyển.

Cho $\bigtriangleup ABC$ nội tiếp $\left ( O \right )$. $H$ là hình chiếu của $A$ lên $BC$. $AO$ cắt $\left ( O \right )$ tại $N$. $NC,NB$ cắt tiếp tuyến của $\left ( O \right )$ tại $A$ ở $P,Q$. $M$ là giao điểm của $BP$ và $CQ$. $AM$ giao $\left ( O \right ), BC$ ở $X,Y$.  $YH$ cắt $\left ( O \right )$ tại $K$. Chứng minh $\frac{YH}{YK}= \frac{XM}{XA}$

Cho $\bigtriangleup ABC$ nội tiếp $\left ( O \right )$. M là điểm chính giữa cung $BC$ nhỏ. $P$ là một điểm nằm trên $\left ( M,MB \right )$. $K,L$ thuộc $AC,AB$ sao cho $AK=AL$. $KL$ cắt $BC,AP$ ở $D,E$. Chứng minh $\left ( BLP \right ),\left ( CKP \right ),\left ( DEP \right )$ có 1 điểm chung khác ngoài $P$

Nguồn Bài toán hay-Lời giải đẹp

Cho $\triangle ABC$ nội tiếp $\left ( O \right )$. Tiếp tuyến tại $B,C$ cắt nhau tại $S$. $M,N$ bất kì thuộc $AC,AB$ sao cho $\overline{M,N,S}$. $I$ là trung điểm $MN$. $AI$ cắt $\left ( O \right )$ tại $K$. Chứng minh rằng $\left ( IKS \right )$ tiếp xúc $\left ( O \right )$