chaobu909

Bài $2$

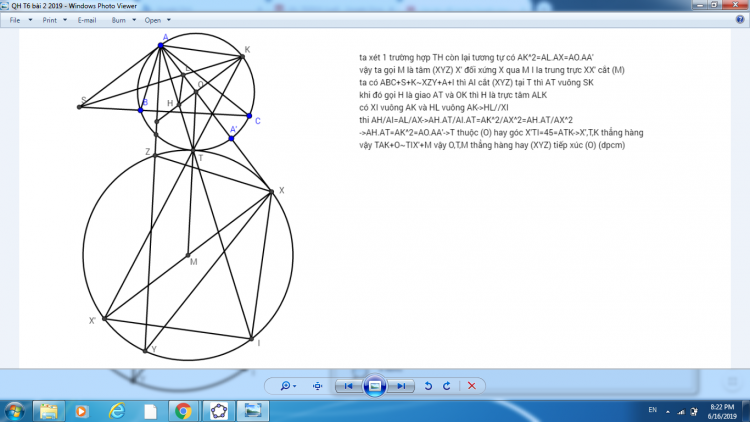
bổ đề 1: Cho tam giác $ABC$, đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$.$K$ là đối xứng $D$ qua $IM$-> $FeK$ đi qua $X$ 

thật vậy ta có $FeDM$~$AIO$ gọi $T$ là trung điểm cung $BC$ không chứa $A$ thì $T'$ đói xứng $T$ qua $BC$ thì $T'XM$~$IDM$->$IT'M$~$KXM$->$KXM=IT'M=TIO=FeDB$->$Fe,X,K $ thẳng hàng

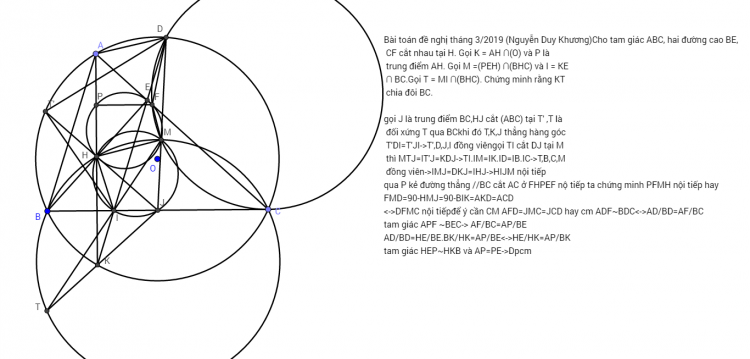
bổ đề 2 và bài giải:

$Bài 2$ 

Bài $2$

 

dạ rồi ạ thế thì em nghĩ phương tích bất kì thì vẫn thu về đồng quy 

Bài $2$ nghịch đảo cực $I$ phương tích r^2 ($r$ là bán kính đường tròn nội tiếp) ta thu về bài toán sau cho tam giác $ABC$ , $I$ là tâm nội tiếp,$D,E,F$ là các tiếp điểm lên $BC,CA,AB$ $I',I1',I2'$ lần lượt là đối xứng $I$ qua $DF,DE,EF$ cmr $JI1',HI',DI2'$ đồng quy với $J,H$ lần lượt là giao $IB,IC$ với $DF,DE$ 

thật vậy do 2 tam giác $JHD$ và $I1'I'I2'$ thấu xạ // nên đồng quy.dpcm

Bài $3$ : P/s bài này căng quá lại 3 câu em mãi mới xong :v 

$a$ ,câu này lời giải không phải của em ạ, của anh nam em xin tóm tắt lại và mở rộng thay điểm $H$ thành điểm $P$ bất kì và hạ $3$ đường vuông góc tạo tam giác $pedal$ ta sử dụng $2$ bổ đề sau 1) gọi $X,Y,Z$ là hình chiếu $P$ lên $BC,CA,AB$ thì gọi điểm bất kì trên $(XYZ)$ qua $P$ kẻ vuông góc cắt 2 cạnh $AB,AC$ tại $M,N$ thì tồn tại 1 inconic tiếp xúc cả $4$ cạnh $AB,BC,CA,MN$ và inconic cố định

2) cho tứ giác $ABCD$ ngoại tiếp $I$ gọi $X,Y,Z,T$ lần lượt là điểm tiếp xúc $(I)$ lên $AB,BC,CD,DA$ thì $AC,BD,XZ,YT$ đồng quy tại 1 điểm

bổ đề 2 vẫn đúng trong inconic nên áp dụng bổ đề $1$ và $2$ ta có điều phải chứng minh  

2 câu $b$,$c$ em tự suy nghĩ ạ, em dùng hình như trong đề  

$b$ ) biến đổi góc ta có điểm $L$ chính là giao $(AEL)$ và $(AFC)$ gọi $U,V$ lần lượt là giao trung trực $HB,HC$ với 2 cạnh $AB,AC$ thì ta sẽ chứng minh $(AUV)$ đi qua $L$ và $(AUV)$ là đường tròn cố định

thật vậy ta có $LFB$~$LCE$ nên ta chỉ cần chứng minh $\frac{UB}{BF}=\frac{EV}{EC}$ 

thật vậy gọi $M,N$ là hình chiếu $K$ lên $AC,BC$ và $KH$ căt $EF$ tại $P$ thì $M,N,P$ thẳng hàng và $KPL$ ~ $KEC$ ~$KFB$ thi $AFEK$ nội tiếp

thì $\frac{BF}{EC}=\frac{KF}{KE}=\frac{HF}{HE}=\frac{UH}{EV}$ vậy ta chứng minh $FHU$ ~ $HEV$ thật vậy cộng góc ta có $HVA=HUA$ và $EHV=BFH$ nên ta có dpcm.

$c$ ta chứng minh $KP$ đi qua giao $2$ tiếp tuyến tại $B$,$C$

 <-> $\frac{KB}{KC}=\frac{KF}{KE}=\frac{BF}{CE}=\frac{BP}{PC}=\frac{BL}{LE}$

thật vậy do tam giác $BFL$ ~ $ECL$ nên ta có đpcm  

Bài 6: bài này dài quá em xin phép không gõ talex ạ :v
a) gọi B’ là đối xứng B qua AI
Từ đó tam giác BFB’ ~EMF nên AM.AB’=AE^2
Nghịch đảo đối xứng cực A phương tích AF^2 ta có M<->B N<->C hay ta đưa bài toán về bài toán sau
Gọi G là tâm A-Mix ,(AGB),(AGC) lần lượt cắt AC,AB tại U,K. Chứng minh rằng MN tiếp xúc (AUK)
Thật vậy gọi H là hình chiếu của G lên MN có tam giác ABI ~ AGM nên biến đổi góc ta có HGM=C/2 hay MN tiếp xúc A-mix. Gọi P là trung điểm CE thì EPIG nội tiếp -> PIG=180-HEG=180-BIG-> B,I,P thẳng hàng.BPG=IEG=BAG-> P thuộc (AGB).GN vuông BI nên BI cắt MN tại 1 điểm trên (G,GB).HLI=ABI=PUE
->U,L đối xứng qua PG.ULHE và IHLE nội tiếp -> 5 điểm thuộc đường tròn -> H thuộc (UIE) tương tự -> H là điểm miquel của AEF -> H thuộc (AKU) và MA.MU=MP.MG=MH^2 -> (AKU) tiếp xúc MN.
b)qua phép nghịch đảo đối xứng ta chỉ cần chứng minh KU//X1Y1
GH/TJ=GE/JL=AG/AJ->A,H,T thẳng hàng
Vậy ta chứng minh GU//JX1
AUG= 180-ABG,AX1J=ANJ=180-ANC
Vậy <->ABG=ANC<->IBG=JAN
Gọi M’ là đối xứng M qua AI -> BM’IG nội tiếp ->IBG=M’BG
Thật vậy có tam giác M’IG~ANJ(cgc) có góc MGI= AJN và tỉ lệ cạnh <-> GME~JCL
-> dpcm .

Bài $5$:

ta sẽ chứng minh 2 kết quả sau: từ đó ta có $TJ$ tiếp xúc với $(BC)$ cố định (dpcm)

kết quả $1$: $TB\perp BC$

kết quả $2$ : $TB$ và $TJ$ đối xứng nhau qua $TM$ từ đó ta có $TJ$ tiếp xúc $(BC)$ 

thật vậy, áp dụng định lí dersagues cho $2$ tam giác $JHZ$ và $XCM$ từ đó ta có $JX,CH,ZM$ đồng quy tại $K$. 

có tam giác $YBZ$ ~ $KCX$ và tam giác $TZY$ ~ $MXK$ từ đó ta có $TYZ^B$ ~ $MKX^C$ nên $TBY=MCK$ hay $TB$ vuông $BC$. vậy $TB$ là tiếp tuyến của $T$ đến $(BC)$

ta chỉ cần chứng minh $BTM=MTJ$ từ đó có kết quả $2$.

tương đường $TJY=YJH$ và có $JY vuông JX$ nên ta chỉ cần chứng minh $J(TH,YX)=-1$ 

gọi $U,V,L$ lần lượt là giao của $BT$ với $JY,JX$ và giao của $BC$ với $JX$

ta chỉ cần chứng minh $J(TH,UV)=-1$ hay $T$ là trung điểm $UV$

tương tự trên ta có  $TYU\bigcap B\bigcap Z$ ~ $MKL\bigcap C\bigcap X$ nên $\frac{TB}{TU}=\frac{MC}{ML}=\frac{MB}{ML}=\frac{BT}{TV}$

vậy $TV=TU$ hay ta chứng minh được bổ đề $2$ áp dụng kết quả $1$ và $2$ ta có dpcm 

P/s : Bài toán thật hay

Bài $4$ : ta chỉ cần chứng minh $TP=TQ$ 

Gọi $BE,CF$ là 2 đường cao từ $B,C$ $PQ$ cắt $BC$ tại $G$.$DK,DL$ cắt $PQ$ tại $H,M$

Bài $1$ : gọi tiếp tuyến là $d$ cắt $AB$,$AC$ tại $K$,$L$.gọi $Ia,Ib,Ic$ lần lượt là tâm bàng tiếp góc $A,B,C$ của tam giác $ABC$ . $M,N,K,U$ là tiếp điểm của $Ib,Ic,Ia$ lên $BC$ Và giao $AD với (IDE)$ $A’$ là đối xứng $A$ qua $O$. Có tam giác $ADI~AIaA’$ -> góc $ADI=AIaA’=KIU$ vậy ta chỉ cần chứng minh $A’Ia$ vuông góc với $XY$ thật vậy $IaX=IaN,IaY=IaM$ -> $IaY^2-IaX^2=IaM^2-IaN^2=MK^2-NK^2$ để ý $MK=AC,NK=AB$ và $AC^2-AB^2=A’B^2-A’C^2$. Vậy theo định lí 4 điểm ta có $XY vuông góc A’Ia$ (dpcm)

Bài $3$ : $IL=IA$ và $JA=KJ$
gọi $X,Y$ là giao đường thẳng qua $K,L$ vuông góc đối trung tại $A$ ta sẽ chứng minh $BX$ $CY$ đi qua đối xứng $A$ qua $O$
thật vậy,Dpcm <-> $ABKX$ nội tiếp
Gọi $T$ là giao của $AK$ với $EF$ hay ta chỉ cần chứng minh $BETK$ nội tiếp
gọi $M$ là trung điểm $AB$,$OM$ cắt trung trực $AK$ tại $H$ khi đó $H$ là trực tâm $ATJ$
gọi $N$ là trung điểm $AK$ khi đó <-> $AM.AE=AN.AT$ <-> $AEF=ANM=AHM$ hay ta cần chứng minh $AH$ vuông $EF$
<-> $TH$ vuông $AJ$ hay ta chứng minh $HT//AB$
áp dụng $\frac{MH}{HO}=\frac{AM}{AO}.\frac{sinA/2}{sin OAH}$ và $\frac{ET}{TO}=\frac{AE}{AO}.\frac{sinBAN}{sinNAO}$

vậy ta chứng minh $\frac{AE}{AM}.\frac{sin DAC}{sinUAD}=\frac{sinA/2}{sinVAO} <->\frac{AE}{AM}.\frac{sinDAC}{sinA/2}=\frac{sin UAD}{sinVAO}=\frac{AV}{AD} =\frac{AE}{AM}.\frac{sin DAC}{sinC}.\frac{sinC}{sinA/2}=\frac{AE}{AM}.\frac{DC}{DA}.\frac{AB}{BV} <-> \frac{2AE.DC}{BV}=AV <->AE.BC=BV.AV$
tương đương tam giac $AEV$ đồng dạng tam giác $BVC$ với $V$ là trung điểm $BC$ không chứa $A$ của $(O)$ (đúng hiển nhiên)
với $U,D$ lần lượt là hình chiếu $A$ lên $BC$ và trung điểm $BC$
-> $HT//AB$ ->$BX,CY$ cắt nhau trên $(O)$ cố định

Bài $5$

bổ đề : $IL$ đi qua $J$ là điểm gergonne

Bài 1: gọi $(BHC)$ cắt $(IHX)$ tại $J$,ta sẽ chứng minh $J$ thuộc $(AIN)$ 

vậy ta sẽ chứng minh góc $IXH$= góc $IAN$ + góc $HBN$

thật vậy gọi $O$ là tâm ngoại tiếp của $(ABC)$ khi đó ta chỉ cần chứng minh góc $MAO$= góc $HBN$ 

ta sử dụng 2 kết quả sau :$1$, gọi $O'$ là tâm $(BHC)$ thì $O'$ la đối xứng của $O$ qua $BC$

$2$, $HO'$ cắt $(BHC)$ tại $K$ thì $K$ là đối xứng của $A$ qua $M$ 

sử dụng 2 kết quả-> $HK$//$AO$ ->góc $OAM$= góc $HKM$= góc $HBN$

Bài $3$ : gọi $D$ là chân đường cao từ $A$ xuống tam giác $ABC$ 

Xét phép nghịch đảo cực $A$ phương tích là $AH.AD$ ta chuyển bài toán về bài toán sau:

cho tam giác $ABC,M$ là trung điểm $BC$ đường thẳng qua $M$ vuông góc $AB$ cắt $AB,AC$ tại $F,K$

đường thẳng qua $M$ vuông góc $AC$ cắt $AC,AB$ tại $R,T$,$H$ là trực tâm tam giác $ABC$ $Hb,Hc$ là hình chiếu $B,C$ lên $AC,AB$

gọi $U$ là giao $(AHbT),(AHcK)$ ta chứng minh $AU$ đi qua đối xứng $O$ là $O'$ qua $BC$ cố định

thật vậy tam giác $HcUT$ ~ $KUHb$ ->$\frac{d/(U/AB)}{d/(U/AC)}=\frac{HcT}{HbK}$

vậy ta chứng minh $\frac{d/(O'/AB)}{d/(O'/AC)}=\frac{HcT}{HbK}$

Gọi $X$ là giao 2 tiếp tuyến tại $B,C$ của $(O)$ ,cộng góc ta có $XT$ vuông $AB$,$XK$ vuông $AC$ 

có $\frac{d/(O'/AB)}{d/(O'/AC)}=\frac{d/(O'/AB)}{BO'}.\frac{CO'}{d/(O'/AC)}$ = $\frac{sin(90+BAC-ABC)}{sin(90+BAC-ACB)}$

$\frac{HcT}{HbK}=\frac{HcT}{MHc}.\frac{MHb}{HbK}=\frac{sinHcMT}{sinBXM}.\frac{sinMXC}{sinHbMK}=\frac{sin HcMT}{sin HbMK}$

có góc $HcMH=2(90-ABC)+90-(180-ABC-BAC)=90+BAC-ABC$

góc $HbMK=2(90-ACB)+90-(180-ACB-BAC)=90+BAC-ACB$

vậy ->$AU$ đi qua $O'$ cố định-> $AZ$ luôn đi qua điểm cố định do $U$ là ảnh nghịch đảo của $Z$ qua phép nghịch đảo cực $A$ phương tích $AH.AD$

Bài $2$:

a) Gọi $B'$ $C'$ lần lượt là đối xứng của $B$ $C$ qua $O$ là tâm ngoại tiếp của tam giác $ABC$

lấy $G$ $T$ là điểm nằm trên $CC'$ $BB'$ sao cho $BG$ $CT$ vuông góc $C'M$ $B'M$ 

$X$ $Y$ là tâm ngoại tiếp tam giác $BGM$ $CTM$ 

ta có $B'M$=$C'M$ và $MX=MY$ 

Bằng cộng góc ta có tam giác $BXM$~$FKM$~$BOC 

, các tứ giác $GOMB$ $MOTC$ nội tiếp và  $BFM$ ~$C'AM$ -> $\frac{XM}{MK}=\frac{BM}{MF}=\frac{C'M}{AM}->XK//AC'$

tương tự ->$AB'//KY$ mà $ A B' C' M $ nội tiếp -> $XKYM$ nội tiếp -> $K$ chạy trên $(XMY)$ cố định 

b) gọi ($BFH$) cắt ($CEH$) tại $D$ cộng góc -> $D$ thuộc (O) và  góc $EDF$ = 2. góc $ABH$ 

gọi $BH$ $CH$ cắt $(O)$ tại $N ,P$ góc $HNE$ = góc $EHN$ =1/2 góc $BAC$ -> $ N,E,M$ thẳng hàng 

tương tự $P,F.M$ thẳng hàng vậy góc $EMF$= 2 góc $ABH$ =góc $EDF$ -> D thuộc (EMF) và góc $EDH$= góc $ABH$= góc $ACH$

=góc $HDF$-> $EH$ là phân giác $EDF$ 

c) Gọi đường thẳng qua $H$ vuông góc $EF$ cắt $BC$ tại $L$ ta sẽ CM $\frac{HL}{IK}=\frac{DH}{DI}$

có tam giác $BHL$~$AEH$ ->$\frac{HL}{EH}=\frac{BH}{AE}$

vậy ta CM $\frac{DH}{DI}=\frac{EH.BH}{AE.IK}<->\frac{DH}{BH}=\frac{sin DFE.sin DIM}{sin AFE} =\frac{sin HBC}{sin(180-1/2BAC-ABC)}=\frac{sin(90-C)}{sin(1/2A+B)}=\frac{sin ABO}{sinABM'}=\frac{AB'}{AM}$

hiển nhiên do tam giác $AEH$~$MAB$ do góc$EAH=AMB$ và $HEA=BAM$ vậy ta có DPCM 

P/s: em không biết ghép hình ntn e ghép rồi nhưng không vào được ạ