1.Liên thông đường
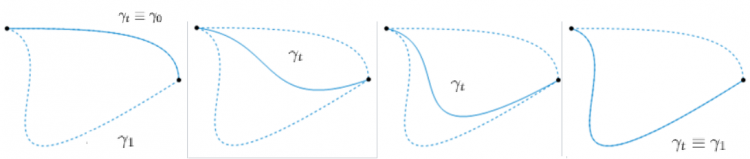
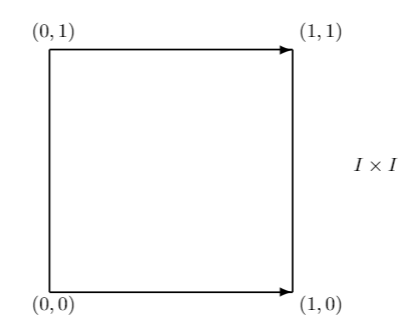
Định nghĩa 1.1 Một đường trong $X$ là một ánh xạ liên tục $f:I\rightarrow X$. Nếu $f(0)=a$ và $f(1)=b$, ta nói $f$ là một đường từ $a$ đến $b$.
Định nghĩa 2.1 Một không gian $X$ được gọi là liên thông đường nếu, với mọi $a,b\in X$, tồn tại một đường trong $X$ từ $a$ đến $b$.
Định lý 1.3 Nếu $X$ liên thông đường thì $X$ liên thông.
Chứng minh
Nếu $X$ không liên thông thì tồn tại $A,B\neq \varnothing$ là các tập mở trong $X$ sao cho $A\cap B = \varnothing$ và $A\cup B=X$. Lấy $a\in A$ và $b\in B$, xét $f:I\rightarrow X$ là một đường từ $a$ đến $b$. Ta có
\[ f(I)=(A\cap f(I))\cup (B\cap f(I)).\]
Do đó $f(I)$ không liên thông. Điều này mâu thuẫn vì $f(I)$ phải liên thông. $\square$
Định lý 1.4 Nếu $f:X\rightarrow Y$ liên tục và $X$ liên thông đường, thì $f(X)$ liên thông đường.
Chứng minh
Ta có, với mỗi $y_{1}$, $y_{2}$ $\in f(X)$ thì tồn tại $x_{1}$, $x_{2}$ $\in X$ sao cho $f(x_{1})=y_{1}$, $f(x_{2})=y_{2}$. Do $X$ liên thông đường nên tồn tại $h:I\rightarrow X$ liên tục sao cho $h(0)=x_{1}$, $h(1)=x_{2}$. Xét hàm $g=f \circ h$, khi đó $g:I\rightarrow Y$ liên tục và $g(0)=y_{1}$, $g(1)=y_{2}$ nên $f(X)$ liên thông đường. $\square$
2. Thành phần đường
Định lý 2.1 Nếu $X$ là một không gian topo, thì quan hệ hai ngôi $\sim$ trên $X$ xác định bởi "$a\sim b$ nếu và chỉ nếu có một đường trong $X$ từ $a$ đến $b$" là một quan hệ tương đương.
Chứng minh
- Tính phản xạ: Nếu $a\in X$, hàm hằng $f:I\rightarrow X$ với $f(x)=a$ $\forall x\in I$ là một đường từ $a$ đến $a$.
- Tính đối xứng: Nếu $f:I\rightarrow X$ là một đường từ $a$ đến $b$, thì $g:I\rightarrow X$ sao cho $g(x)=f(1-x)$ $\forall x \in I$ là một đường từ $b$ đến $a$.
- Tính bắc cầu: Nếu $f$ là một đường từ $a$ đến $b$ và $g$ là một đường từ $b$ đến $c$ thì $h:I\rightarrow X$ xác định bởi:
\[ h(t)= \begin{cases} f(2t) \ \text{nếu}\ 0\leq t\leq 1/2 \\ g(2t-1) \ \text{nếu}\ 1/2 \leq t\leq 1.\end{cases}\]
khi đó $h$ liên tục nên $h$ là đường từ $a$ đến $c$. $\square$
Định nghĩa 2.2 Các lớp tương đương trong $X$ xác định dưới quan hệ tương đương $\sim$ trong định lí trên được gọi là các thành phần đường trong $X$.
Các thành phần đường của $X$ là các tập con liên thông đường lớn nhất của nó. Hơn nữa, mọi tập con liên thông đường của $X$ là tập con của một thành phần đường duy nhất của $X$.
Định nghĩa 2.3 Ta sẽ kí hiệu tập các thành phần đường trong $X$ là $\pi_{0}(X)$. Đồng thời xác định $\pi_{0}(f):\pi_{0}(X)\rightarrow \pi_{0}(Y)$ là ánh xạ biến mỗi thành phần đường $C\subset X$ thành một thành phần đường của $Y$ chứa $f(C)$.
Định nghĩa ánh xạ $\pi_{0}(f)$ ở trên là một định nghĩa tốt do ảnh của một tập liên thông đường qua một ánh xạ liên tục cũng là một tập liên thông đường, hơn nữa chỉ có duy nhất một thành phần đường $Y$ chứa $f(C)$.
Định lý 2.4 $\pi_{0}:\textbf{Top} \rightarrow \textbf{Sets}$ là một hàm tử. Hơn nữa, nếu $f\simeq g$, thì $\pi_{0}(f)=\pi_{0}(g)$.
Chứng minh
Chúng ta dễ dàng kiểm tra rằng $\pi_{0}$ bảo toàn phần tử đơn vị và bảo toàn phép hợp thành, từ đó kết luận được $\pi_{0}$ là một hàm tử.
Nếu $f\simeq g$ thì tồn tại $F:X\times I\rightarrow Y$ liên tục sao cho $F(x,0)=f(x)\forall x\in X$ và $F(x,1)=g(x)\forall x\in X$. Nếu $C$ là thành phần đường của $X$ thì $C\times I$ là liên thông đường, nên $F(C\times I)$ là liên thông đường. Ta có:
\[ f(C)=F(C\times {0})\subset F(C\times I)\quad \text{và} \quad F(C\times I)\supset F(C\times {1})=g(C).\]
Khi đó, thành phần đường $Y$ chứa $F(C\times I)$ cũng chứa $f(C)$ và $g(C)$. Vậy nên $\pi_{0}(f)=\pi_{0}(g)$. $\square$
Hệ quả 2.5 Nếu $X$ và $Y$ có cùng dạng đồng luân thì $\pi_{0}(X)$ đẳng cấu với $\pi_{0}(Y)$.
Định nghĩa 2.6 Một không gian $X$ được gọi là liên thông đường địa phương nếu, $\forall x\in X$ và mọi lân cận mở $U$ chứa $x$, tồn tại một tập mở V với $x\in V\subset U$ sao cho bất kì hai điểm nào trong $V$ cũng có một đường trong $U$ đi từ điểm này đến điểm kia.
Định lý 2.7 Một không gian $X$ là liên thông đường địa phương nếu và chỉ nếu các thành phần đường của một taappj mở là tập mở. Nói riêng, nếu $X$ liên thông đường địa phương thì các thành phần đường của nó đều mở.
Chứng minh
Giả sử $X$ là liên thông đường địa phương và $U$ là một tập mở trong $X$. Lấy $C$ là một thành phần đường trong $U$, và với mỗi $x\in C$ tồn tại một tập mở $V$ sao cho $x\in V\subset U$ thỏa mãn với mỗi điểm trong $V$ thì đều có một đường từ điểm đó tới $x$ trong $U$. Vì thế mỗi điểm trong $V$ đều thuộc cùng một thành phần đường chứa $x$ nên $V\subset C$. Vậy, $C$ mở.
Ngược lại, cho $U$ là một tập mở trong $X$, với $x\in U$, gọi $V$ là thành phần đường của $x$ trong $U$. Theo giả thiết $V$ mở. Vậy nên $X$ là liên thông đường địa phương. $\square$
Hệ quả 2.8 $X $ liên thông đường địa phương nếu vầ chỉ nếu, với mỗi $x\in X$ và với mỗi lân cận mở $U$ của $x$ tồn tại một tập mở liên thông đường $V$ sao cho $x\in V\subset U$.
Hệ quả 2.9 Nếu $X$ liên thông đường đại phương thì các thành phần của mỗi tập mở trùng với các thành phần đường của nó. Đặc biệt, các thành phần của $X$ trùng với các thành phần đường của $X$.
Hệ quả 2.10 Nếu $X$ liên thông và $X$ liên thông đường địa phương thì $X$ liên thông đường.
- Zaraki, Syndycate và Lemonjuice thích



 Tìm kiếm
Tìm kiếm Nam
Nam














 Gửi bởi
Gửi bởi