duylax2412

Bài 3: (Cách giải hoàn toàn cấp 2)
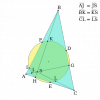
a) Dễ thấy tam giác $AMQ$ cân tại $M$ nên $\widehat{DPQ}=\widehat{DMQ} $ (cùng phụ $\widehat{BAC}$
Nên tứ giác $MPDQ$ nội tiếp. Tương tự $MDNQ$ nội tiếp nên (C) qua $D$ cố định
b) Gọi $J$ là trung điểm $MN$ và $I$ là tậm (C)
Lấy $L$ đối xứng $M$ qua $D$ thì $C$ là trực tâm $LDN$ . Suy ra $JD \bot BC$ và $JD=\frac{LN}{2}=\frac{CD.tanA}{2}$ ( chú ý $\widehat{LDN}=\widehat {A}$)
Nên $J$ cố định. Gọi $K$ là trung điểm $AD$ và $Z$ là trung điểm DJ; X,Y là trung điểm DB,DC
Khi đó $K,I$ đối xứng qua Z. Mà $\widehat{XKY}=\widehat{BAC}$ nên K di động trên đường tron $(T)$ cố định
Nên $I$di động trên đường tròn có tâm đối xứng với tâm đường tròn $(T)$ qua Z cố định

Giả sử n có nhiều hơn 3 ước. Gọi k là ước lẻ lớn nhất của n. Khi đó tồn tại số a|n, a>1 và (a,k)=1 sao cho a+k-1 | n. 

Mà a+k-1 > k $\Rightarrow$ k không phải ước lớn nhất của n (vô lý) 

$\Rightarrow$ n=$k^x$ với k là số nguyên tố lẻ và x là số nguyên dương

Chưa chắc đã tồn tại số a như thế đâu. Ví dụ 45 có ước lẻ lớn nhất là 15 nhưng không có ước nào của nó nguyên tố cùng nhau với 15 (trừ 1)
Giả sử $n$ không là lũy thừa số nguyên tố. Đặt $n=p^{k}.m$ với $p$ là ước nguyên tố nhỏ nhất của $n$ , $(m,p)=1$; m>1 ;với q là ước nguyên tố nào đó của m thì q không là ước p-1 $\rightarrow q$ không là ước $p+m-1$.Nghĩa là $(p+m-1,m)=1$

Có $p+m-1 |n \Rightarrow p+m-1 | p^k$ .
$(p+m-1,m)=1 \Rightarrow p+2m-2| p^k$ ( do (p+2m-2,m)=1)

Suy ra $p$ có dạng $2p^s-p^r$ với $s,r >1$ vô lý

Hướng giải : Gọi $C'M $ cắt $A_1A'$ tại $S$. 

Ta có $ \triangle BMA_1 \sim \triangle IAC$ và $\triangle IAC' \sim \triangle ICA'$

Từ đó $\frac{BM}{BA_1}= \frac{IA}{IC}=\frac{AC'}{A'C}=\frac{BC'}{BA'}$ 

Nên $\triangle BMC' \sim \triangle BA_1A'$. Suy ra $\widehat{BA'A_1}=\widehat{BC'S}$ tức S thuộc $(\omega)$

Tương tự $C'M $ cắt $B_1B'$ tại điểm thuộc $(\omega)$ nên có đpcm

Người ta bảo tìm giá trị nhỏ nhất n mà. Lạ thay mình cũng ra $8$??

Gọi các thành viên là $1,2,..,n$ và các ngôn ngữ là $L_1;L_2;...;L_{14}$. Thiết lập bảng vuông $n$ dòng là các thành viên ; $14$ cột là các ngôn ngữ

Điền vào ô $ (L_i;j)$ số $1$ nếu $j$ nói được tiếng $L_i$ và số $0$ trong trường hợp ngược lại. Gọi $d(L_i)$ là số các số 1 điền vào cột $L_i$ ($d(L_i)\leq \frac{n}{2}$)

Mỗi cột có $\binom{d(L_i)}{3}$ bộ ba số $1$. Vậy trên bảng có tối đa $14\binom{\frac{n}{2}}{3}$ bộ ba số $1$ cùng cột

Với $3$ hàng tùy ý, luôn có  một cột có $3$ ô đánh số 1 ứng với ba hàng đó. Nên số các bộ ba ô điền số $1$ cùng cột $\geq$ số bộ ba hàng là $\binom{n}{3}$ Suy ra $\binom{n}{3} \leq 14\binom{\frac{n}{2}}{3} \Rightarrow n \geq 8$

$n=8$ chỉ ra như trên

 

 

Cho đường tròn $(O)$ và dây $AB$ cố định. Gọi $C$ là điểm chính giữa cung $AB$.Đường thẳng $(d)$ thay đổi qua $C$ cắt tiếp tuyến tại $A$ và $B$ lần lượt ở $D$ và $E$.$AE$ cắt $BD$ tại $Q$ và đường thẳng $(d)$ cắt $(O)$ tại $P$ Chứng minh $PQ$ luôn đi qua 1 điểm cố định khi $d$ thay đổi  (dễ đoán là trung điểm AB nhưng chưa tìm ra cách chứng minh  )

Chứng minh bằng quy nạp rằng với mọi số nguyên dương $n$ thì tồn tại $x$ nguyên dương sao cho $3^n| 10^x+2$

Kiểm tra $n=1,2,3$. Giả sử với $n$ thì tồn tại $x$ thỏa. Xét $n+1$

Nếu $3^{n+1} | 10^x+2$ thì có đpcm. Xét $3^{n+1}$ không là ước $10^x+2$ thì do $10^x+2$ chia hết $3^n$ nên $10^x+2 \equiv 3^n;2.3^n (mod 3^{n+1})$

Xét hai số $3^{n-2}k$ và $3^{n-2}(k+1)$ trong đó $(k,3)=(k+1,3)=1$

Áp dụng bổ đề $LTE$ thì $v_3(10^{3^{n-2}k} -1)=v_3(10^{3^{n-2}(k+1)} -1)=n$

Do đó $10^{3^{n-2}k} -1;10^{3^{n-2}(k+1)} -1 \equiv 3^n;2.3^n (mod 3^{n+1})$

Mặt khác giả sử $10^{3^{n-2}k} -1 \equiv 10^{3^{n-2}(k+1)}-1 (mod 3^{n+1})$ suy ra $ 10^{3^{n-2}}-1$ chia hết $3^{n+1}$

Vô lý vì $v_3(10^{3^{n-2}} -1)=n < n+1$. Vậy $10^{3^{n-2}k} -1;10^{3^{n-2}(k+1)} -1$ nhận các số dư $mod 3^{n+1}$ khác nhau và thuộc $3^n;2.3^n$. 

Nếu $10^x+2 \equiv 3^n (mod 3^{n+1})$. Chọn $d=3^{n-2}k$ nếu $10^{3^{n-2}k} -1 \equiv 2.3^n (mod 3^{n+1})$ hoặc $d=3^{n-2}(k+1)$ nếu $10^{3^{n-2}(k+1)} -1 \equiv 2.3^n (mod 3^{n+1})$

Lúc đó $2(10^d-1) \equiv 4.3^n \equiv 3^n.10^d (mod 3^{n+1})$. Đặt $x'=x+d$

Từ $10^x+2 \equiv 3^n (mod 3^{n+1})$ suy ra $10^{x'}+2.10^d \equiv 3^n.10^d \equiv 2(10^d-1) (mod 3^{n+1})$

Suy ra $10^{x'}+2 $ chia hết $3^{n+1}$

Nếu $10^x+2 \equiv 2.3^n (mod 3^{n+1})$. Chọn $d=3^{n-2}k$ nếu $10^{3^{n-2}k} -1 \equiv 3^n (mod 3^{n+1})$ hoặc $d=3^{n-2}(k+1)$ nếu $10^{3^{n-2}(k+1)} -1 \equiv 3^n (mod 3^{n+1})$ thì lý luận như trên cũng ra

Tóm lại theo quy nạp , nhận xét chứng minh .

Quay lại bài toán , tồn tại $k$ sao cho $3^{2017} |10^k+2| 3.10^k+6$

Dễ thấy tổng các chữ số $3.10^k+6$ là $9$

 

 

Bài này mình có dùng định lý $Carnot$ về tam giác $Pedal$ : Cho tam giác $ABC$. Các điểm $L,M,N$ lần lượt là ba điểm nằm trên ba cạnh $BC,CA,AB$ của tam giác, khi đó ba đường thẳng qua $L,M,N$ tương ứng và vuông góc với ba cạnh $BC,CA,AB$ đồng quy khi và chỉ khi

$AN^2+BL^2+CM^2=NB^2+LC^2+MA^2$. (nguồn Wikipedia)

Chứng minh bằng $Pytago$

Quay lại bài toán. Thì theo định lý trên ở chiều thuận , ta có:

$AH^2+BD^2+CF^2=BH^2+CD^2+AF^2$

Rõ ràng là cần chứng minh :

$AI^2+BE^2+CG^2=AG^2+BI^2+CE^2$ (để áp dụng định lý đảo)

Hay đi chứng minh 

$(AH^2+AI^2)+(BD^2+BE^2)+(CF^2+CG^2)= (AF^2+AG^2)+(BH^2+BI^2)+(CE^2+CD^2)$

Có $AH.AI=AG.AF;BD.BE=BI.BH;CF.CG=CD.CE$ (phương tích)

Từ đó có biến đổi sau:

$(AH^2+AI^2)+(BD^2+BE^2)+(CF^2+CG^2)=HI^2+DE^2+GF^2+2(AH.AI+BD.BE+CF.CG)$

$(AF^2+AG^2)+(BH^2+BI^2)+(CE^2+CD^2)=GF^2+HI^2+DE^2+2(AF.AG+BH.BI+CE.CD)$

Suy ra điều cần chứng minh.

 

 

Giả sử $CB<CA$ và do đó $T,B$ cùng phía so với $OP$.Gọi $(PCF)$ cắt $(PDE)$ tại $T$

Ta có biến đổi sau $\widehat{CTE}=\widehat{TCF}-\widehat{TEC}=(180^o-\widehat{TPF})-(180^o-\widehat{TPD})=\widehat{DPF}=\frac{1}{2}\widehat{DPE}=\frac{1}{2}\widehat{DTE}$

Suy ra $TC$ là đường phân giác trong $\triangle TDE$

Do đó $\frac{TD}{TE}=\frac{CD}{CE}=\frac{AD}{BE} \Rightarrow \triangle TDA \sim \triangle TEB$. Suy ra $T$ thuộc $(PAB)$

Sao có kết qủa này vậy bạn?

 

Bạn chứng minh $IDQC$ nội tiếp

Ta có kết quả quen thuộc $BP \bot AI$ và $CQ \bot AI$

Từ đó tứ giác $ABHP$ nội tiếp. Suy ra $\widehat{PHM}=\widehat{BAI}$ $(1)$

Gọi $T$ là trung điểm $AC$ thì $\widehat{TQA}=\widehat {TAQ}=\widehat{BAI} \Rightarrow QT \parallel AB$

Từ đó $QM$ đi qua $T$. Vậy $\widehat{MQP}=\widehat{BAI}$ $(2)$

Từ $(1)$ và $(2)$ suy ra P,M,Q,H thuộc 1 đường tròn

Cho số nguyên tố $p$ lẻ và $p\equiv 1\left ( mod 4 \right ).$ Chứng minh rằng số $A=\sum_{k=1}^{\frac{p-1}{2}}k.\binom{p}{k}$ là bội của $p^{2}.$

Xét $k. \binom{p}{k}=p.\frac{(p-k+1)(p-k+2)...(p-1)}{(k-1)!} $

Chú ý $(p-k+1)(p-k+2)...(p-1) \equiv (-1)(-2)...(-k+1) \equiv (-1)^{k-1}.(k-1)! (mod p)$

Và $((k-1)!,p)=1 $ (với $k<p$)

Từ đó $k. \binom{p}{k}=p.\frac{(p-k+1)(p-k+2)...(p-1)}{(k-1)!} \equiv p.(-1)^{k-1} (mod p^2) $

Suy ra $A \equiv p.[ (-1)^0+(-1)^1+...(-1)^{\frac{p-3}{2}} ]\equiv 0 (mod p^2)$ (với $p$ chia 4 dư 1)

Quy nạp thôi

Với $n=3$ thì dễ chỉ ra.

Giả sử với $n$ thì mọi số nguyên dương $>2$ và không quá $n!$ đều biểu diễn được thành tổng không quá $n$ số nguyên dương phân biệt là ước $n!$

Xét $ n!+1 \leq k \leq (n+1)!$ (vì $k \leq n!$ đã đúng theo giả sử)  Thực hiện phép chia $k$ cho $n+1$ với số dự $r$ và thương $t$, tức $k=(n+1)t+r (0 \leq r \leq n)$

Dễ thấy $t \leq n!$ nên theo giả thiết quy nạp tồn tại $a_1;a_2;...;a_m (m \leq n)$ đôi một phân biêt sao cho $t=a_1+a_2+...+a_m$ với $a_i |n! \forall i=\overline{1;n}$

Thì $k=(n+1)a_1+(n+1)a_2+...+(n+1)a_m +r$ cũng là tổng không quá $n+1$ số nguyên dương và dễ thấy các số này phân biệt và là ước $(n+1)!$

Theo nguyên lý quy nạp là xong

 

Gọi $p$ là số nguyên tố nhỏ nhất không là ước $n$ . Dễ thấy $a_1=1$ ;$a_2=p$ và $a_{k}=n-1$

Từ đó suy ra $a_2-a_1=...=a_k-a_{k-1}=p-1$. Tính được $a_{k}=(k-1)(p-1)+a_1$ hay $n-2=(k-1)(p-1)$

Nếu $p=2$ thì suy ra $a_1;a_2;...;a_k$ là các số $1,2,...,n-1$ và nguyên tố cùng nhau với $n$. Vậy $n$ là số nguyên tố

Nếu $p \geq 3$. Gọi $q$ là một ước nguyên tố bất kì của $p-1$ . Do $q<p$ nên theo cách chọn $p$ , ta có $q|n$. Mà $q|p-1|n-2$ nên $q=2$

Nghĩa là $p-1$ chỉ có ước nguyên tố là 2 nên là lũy thừa của $2$ . Đặt $p=2^{m}+1$. Để $p$ nguyên tố thì $m$ phải là lũy thừa của $2$ nên $p$ phải có dạng $p=2^{2^t} +1$

Xét $p>3$ thì $a_3=p-1+a_2=2p-1=2^{2^{t}+1}+1$ chia hết $3$. Mà $n$ cũng chia hết $3$ (do $p$ là số nguyên tố nhỏ nhất không là ước $n$)

Vô lý bởi $(a_3,n)=1$

Vậy $p=3$ từ đó $n$ nguyên tố cùng nhau với $1,3,5,..,n-1$ nên $n$ là lũy thừa $2$

Korkot, câu b, ý tưởng thế nào vậy , giúp mình nhé

Đây là ý tưởng

Giả sử $(a+1)^3-a^3=3a^2+3a+1=n^2$ thì biến đổi ra $3(2a+1)^2=(2n-1)(2n+1)$. Rồi chú ý $(2n-1,2n+1)=1$

Lập luận suy ra $2n-1=(2k+1)^2 $ (là số chính phương lẻ ) 

Câu c)

Dễ dàng chứng minh tứ giác $MPNQ$ nội tiếp.Kẻ đường kính $AK$ (đáng lẽ điều này đã thực hiện ở câu a)

Thì $\widehat{BHP}=\widehat{CHK}=\widehat{NKB}$

Từ đó $\triangle BHP \sim \triangle NKB \Rightarrow \frac{BP}{BN}=\frac{HB}{KN}=\frac{KC}{KN} \Rightarrow  \triangle NBP \sim \triangle NKC$

Do đó : $\widehat{BNP}=\widehat{KNC}$

Kẻ tiếp tuyến $Nx$ tại $N$ của $(O)$ (sao cho $B$ nằm trong $\widehat{PNx}$)

$\widehat{PNx}=\widehat{BNx}+\widehat{BNP}=\widehat{NCM}+\widehat{KNC}=\widehat{NMP}$. Suy ra $Nx$ cũng là tiếp tuyến tại $N$ của $(MPQ)$

Vậy $(MPQ)$ tiếp xúc $(O)$ (và tại $N$)

 

Hình như chỗ này bị sai!

Ừ mình sửa lại r đó. Bạn xem đi (ở đây nhé không phải ở trên)