thailungvan123

Lời giải bài 1 :

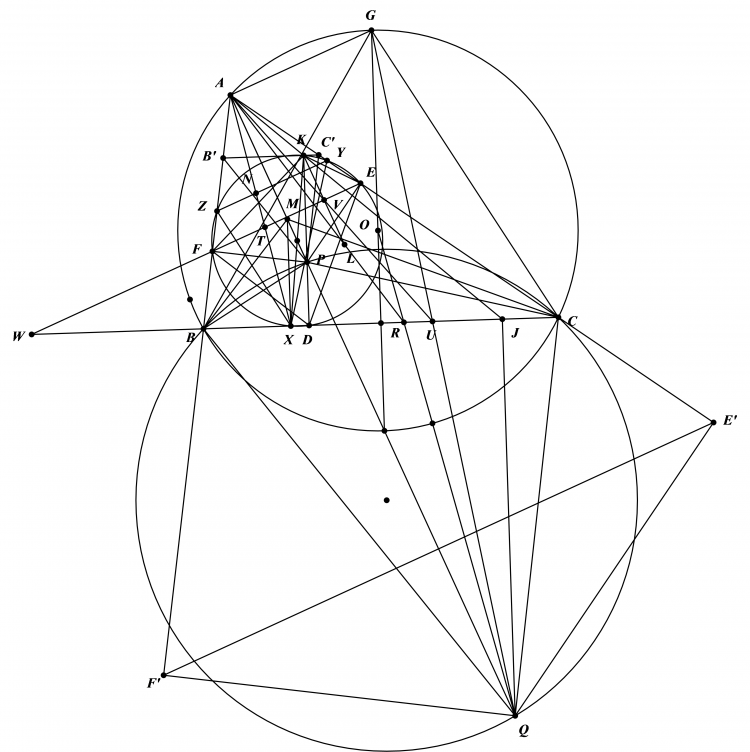
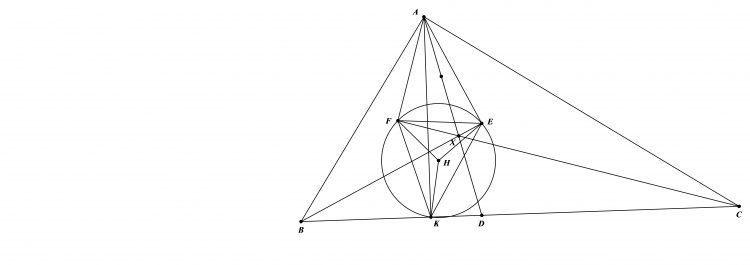
Gọi $Q,Q',P,E,F$ là cung lớn và nhỏ $BC$ ,trung điểm $BC,AO,IQ$  . $JM\parallel  IK$ nên $J$ là trung điểm $AK$

Ta có $IOPK$ nội tiếp nên $\widehat{IKO}=\widehat{IPQ}=\widehat{AIQ}$ do $Q'I^2=Q'Q.Q'P=> \Delta IOK \sim \Delta KQI  =>\Delta MJE \sim \Delta MIF =>\Delta MJI\sim \Delta MEF$

 Ta có $OF\perp AQ$ nên $\Delta MEF$ cân tại $E$ nên tam giác $MIJ$ cân tại $J$

Hạ đường cao $NX,IY,AZ$ của tam giác $INA$, $XY$ cắt $AI$ tại $T$

Ta có $MT.MZ=MI^2=MJ.MN$ suy ra $TJ \perp MN$

Mặt khác $ZT.ZM=ZI.ZA=ZN.ZH$ nên $T$ là trực tâm tam giác $MNH$ $=>$ $HT \perp MN$ $=>T,H,J$ thẳng hàng và $\perp MN$

Nên $JH \parallel OI$

(Hình gửi kèm)

Em có lời giải bài 1 :

$AK$ cắt $BC$ tại $J$ .Từ $K$ kẻ song song $BC$ cắt $AB,AC$ tại $B',C'$ từ đó $\widehat{CBQ}=\widehat{CPQ}=\widehat{KFP}=\widehat{C'B'P}$ nên ta có $V_{A}^{\frac{AB}{AB'}}:AB'C' \rightarrow ABC ,P\rightarrow Q,K\rightarrow J$ . nên $QJ \perp  BC$ . Gọi $G$ là điểm chính giữa cung $BC$ ,$KL$ cắt $FE$ tại $V$,$AV$ cắt $BC$ tại $U$

Ta sẽ chứng minh $QR$ đy qua $O$ là tâm ngoại $ABC$ . Mà lại có :$A(KLVQ)=-1 => Q(UPRJ)=-1$ nên ta cần chứng minh $QU$ đi qua $G$ .

Gọi $M$ đẳng giác với $P$ trong tam giác $ABC$ và $X,Y,Z$ là hc của $M$ trên $BC,CA,AB$

Bằng góc ta có thể chứng minh $\bigtriangleup KEF \sim \bigtriangleup MBC$ nên $\frac{XB}{XC}=\frac{VE}{VF}$

Mặt khác  $\bigtriangleup MBX \sim \bigtriangleup PBF$ nên ta cũng có $\frac{XB}{XC}=\frac{BF}{CE}$ nên khi $EF$ cắt $BC$ tại $W$ thì  $(WXBC)=-1$

Mặt khác $\frac{BU}{CU}=\frac{AB.Sin\widehat{BAV}}{AC.Sin\widehat{CAV}}=\frac{AB.CE}{AC.BF}=\frac{WE}{WF}=\frac{TE}{TF}$

(Do 2 đẳng thức trên +$Menelaus$ và $T$ là giao của $AX$ và $FE$)

 Ta có $\widehat{ABQ}=\widehat{AZX},\widehat{AYX}=\widehat{ACQ}$ nên $AZXY \sim ACQB$ , Gọi $GQ$ cắt $BC$ tại $U'$. $YZ$ cắt $AX$ tại $N$ tài có $\frac{U'B}{U'C}=\frac{NY}{NZ}=\frac{TE}{TF}=\frac{UB}{UC}$ nên $U \equiv U'$ 

Vậy $Q,U,G$ thẳng hàng , kết hợp hàng điều hòa nên $Q,R,O$ thẳng hàng

(Hình gửi kèm)

Mình xin đề xuất bài tiếp theo:

Bài toán 190: Cho tam giác $ABC$ nội tiếp $(O),$ ngoại tiếp $(I),$ phân giác $AD,BE,CF.X,Y,Z$ lần lượt thuộc $BC,CA,AB$ sao cho $IX,IY,IZ$ lần lượt vuông góc với $AI,BI,CI.$ Chứng minh rằng $(ADX),(BEY),(CFZ)$ đồng trục.

Lời giải bài 189 :   Theo bài toán 188, $\widehat{HKG}=\widehat{BAD}+\widehat{ACB}=\widehat{ACB}+\widehat{CAG}=\widehat{AGK}$ nên $KH$ đi qua trung điểm $AG.$

Lời giải bài 188. Gọi $K$ là chân đường cao từ $A$ thì $\widehat{FKE}=\widehat{EKB}-\widehat{FKB}=180-\widehat{BAE}-\widehat{FAC}=90-\widehat{FAE}=\frac{\widehat{FHE}}{2}$ nên $H$ là tâm ngoại tam giác $KEF$ Nên $\widehat{HKD}=\widehat{HKE}+\widehat{EKC}=90-\widehat{KFE}+\widehat{BAE}=\widehat{BAE}+90-\widehat{AFK}+\widehat{AFE}=\widehat{ACB}+\widehat{BAD}=Const$ nên đường $HK$ cố định , có dpcm