MoMo123

Schur
$a^3+b^3+c^3 +3abc \geq ab (a+b)+bc(b+c)+ca(c+a) \geq 2 ( \sum ab\sqrt {ab}) \geq 6$

cho $x\geq 1$ $y\geq 2$  $z\geq 3$ Tim max P=$\frac{xy\sqrt{z-4}+yz\sqrt{x-2}+xz\sqrt{y-3}}{xyz}$

 

Điều kiện của các biến có vấn đề nên đề chắc chưa chuẩn đâu.Hoặc dấu bằng không xảy ra.

$P=\frac{\sqrt{z-4}}{z}+\frac{\sqrt{x-2}}{x}+\frac{\sqrt{y-3}}{y}=>P.\sqrt{5}=\frac{\sqrt{(z-4).5}}{z}+\frac{\sqrt{(x-2).5}}{x}+\frac{\sqrt{(y-3).5}}{y}\leq \frac{z-4+5}{2z}+\frac{x-2+5}{2x}+\frac{y-3+5}{2y}=\frac{3}{2}+\frac{1}{2z}+\frac{3}{2x}+\frac{1}{y}\leq \frac{3}{2}+\frac{1}{6}+\frac{3}{2}+\frac{1}{2}=\frac{22}{6}=>P\leq \frac{22\sqrt{5}}{30}$

Dấu bằng không xảy ra

Hình như dấu bằng không xảy ra tại điều kiện thì phải   (Hơn nữa cũng không chuẩn cho lắm vì nếu $x=1,y=2,z=3$ thì vô nghĩa dấu căn rồi còn đâu )

$\frac{xy\sqrt{z-4}}{xyz}=\frac{xy\sqrt{(z-4).4}}{2zyz} \leq \frac{xy.(z-4+4)}{4xyz} =\frac{1}{4}$

Thiết lập các BĐT tương tự, ta có $ P \leq \frac{1}{8}+\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{3}}$

Dấu bằng xảy ra tại $x=4 \,\,\, z=8 \,\,\, y=6$

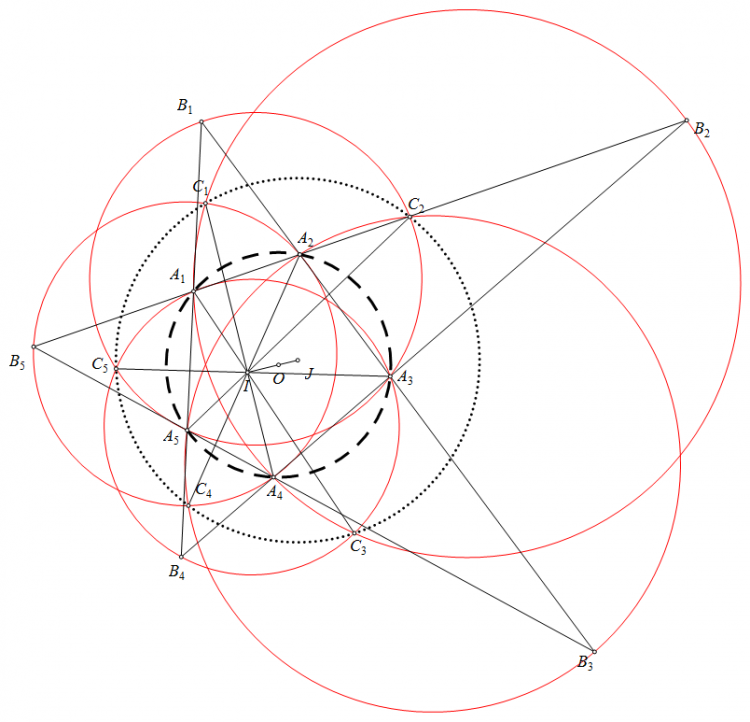
Bài Toán (Đào Thanh Oai) Cho ngũ giác $A_{1}A_{2}A_{3}A_{4}A_{5}$ nội tiếp đường tròn $(O)$. Đặt $B_{i}= A_{i-1}A_{i} \cap A_{i+1}A_{i+2}$ với mọi $i=\overline{1;5}$. $(O_{i})$ là đường tròn qua $B_{i}, A_{i+2},A_{i+4}$ . $C_{i}$ là giao thứ 2 của $(O_{i+1})$ và $(O_{i+4})$.

Chứng minh $C_{1},C_{2},C_{3},C_{4},C_{5}$ cùng thuộc một đường tròn.

Mở rộng của anh baopbc: a)$A_{i}C_{i+2}$ đồng quy tại I

                                          b) Gọi $J$ là tâm $(C_{1}C_{2}C_{3}C_{4}C_{5})$. Chứng minh $O,I,J$ thẳng hàng

P/s: Anh baopbc cũng đã đăng lên nhưng mình xin phép được đăng lại để mọi người tham khảo 

Chào mọi người , chào topic của anh , I'm back. Lâu nay mình lo ôn thi nên hơi bỏ bê $\boxed{\text{TOPIC}}$ cảm ơn mọi người vì đã chăm sóc nó chu đáo. Kỳ thi chuyên đã qua, tuy có một số chuyện buồn, chuyện vui trong thi cử, nhưng mà ta đều phải quên đi để ''bung lụa'' mà tận hưởng mùa hè chứ . Đùa thôi, mình muốn nói rằng hệ thống ôn chuyên đã đóng lại, để ngăn chặn việc spam làm loãng cũng như tính mĩ quan của $\boxed{\text{TOPIC}}$, mình xin thông báo rằng mình sẽ khóa $\boxed{\text{TOPIC}}$ vào thời điểm này. Chúc mọi người có một kì nghỉ hè vui vẻ và bổ ích .

                                            Chúc mừng $\boxed{\text{TOPIC}}$ đạt 2 tháng 5 ngày tuổi

 

$$-MoMo123-$$

Hey everybody, I'm back . Như chúng ta đã biết, các kì thi chuyên đã hoàn thành xong gần hết và hệ thống ôn chuyên đã đóng lại. Thật là vui khi có thể cùng nhau thảo luận về các bài Toán hay cũng như tranh luận chúng. Mặc dù rất tiếc nhưng để ngăn chặn tình trạng spam, mình vẫn phải thông báo rằng mình sẽ khóa topic tại thời điểm này. Chúc các bạn một mùa hè bổ ích, chúng ta sẽ gặp lại nhau trong topic ôn hè sắp tới (gần lộ rồi ).

                                             $$-MoMo123-$$

Cho $p$ là số nguyên tố lẻ. Gọi n là số các số chẵn nằm trong khoảng $(\frac{p}{2};p)$. Chứng minh rằng:

$$ 2^{\frac{p-1}{2}} \equiv (-1)^n (mod \, p)$$

P/s : Lâu lâu nghịch lại thặng dư cũng hay hay(đùa  )

Chú ý: Không dùng thặng dư bình phương   để giải, hãy nêu một cách giải khác

 

Có trong sách Tài liệu chuyên toán giải tích 12 đó em. Em tham khảo trong đó

Ở đây em muốn nói đến cách không dùng thặng dư thôi , vì nó phức tạp mà đi thi mà chứng minh được mấy cái này cũng lòi mắt ra

 

Solution:

Giả sử $t_{1}; t_{2}; ....; t_{n}$ là các số chẵn trong khoảng $(\frac{p}{2};p)$ 

Vậy $ p-t_{1}; p-t_{2} ;......; p-t_{n}$ là các số lẻ trong khoảng $(0;\frac{p}{2})$

Gọi $q_{1}; q_{2}; ......; q_{m}$ là các số chẵn trong khoảng $(0;\frac{p}{2})$

Thì $m+n =\frac{p-1}{2}$

Ta có : Tập hợp $A=\left\{q_{1},q_{2},....,q_{m}, p-t_{1},p-t_{2},...p-t_{n} \right\}$ thì 

$A=\left\{1,2,.....,3,\frac{p-1}{2} \right\}$ 

Nên $q_{1}q_{2}...q_{n}(p-t_{1})(p-t_{2})...(p-t_{n}) =(\frac{p-1}{2})!$                                                                                              $(1)$

Mặt khác ta thấy $q_{1}q_{2}...q_{m}(p-t_{1})(p-t_{2})...(p-t_{n}) \equiv q_{1}q_{2}...(-t_{1})(-t_{2})...(-t_{n}) \,\,\,\, (mod p)$

$\Leftrightarrow q_{1}q_{2}...q_{m}(p-t_{1})(p-t_{2})...(p-t_{n}) \equiv (-1)^nq_{1}q_{2}...q_{m}t_{1}t_{2}...t_{n}\,\,\,\,(mod p)$                            $(2)$

Vì $q_{1},..,q_{m}; t_{1},...t_{n} $ là các số chẵn trong khoảng $(0;p)$

Nên $q_{1}...q_{m}t_{1}...t_{n}=2.4.6....(p-1)$

                                              $=(2.1)(2.2)(2.3)(2.4)...(2.\frac{p-1}{2})$

                                              $=2^{\frac{p-1}{2}}.(\frac{p-1}{2})!$                                                                  $(3)$

Từ$ (1)(2)(3)  \Rightarrow 2^{\frac{p-1}{2}} \equiv (-1)^n         \,\,\,\, (mod p)$

Cái này là tính chất của thặng dư bình phương thôi.
Có:
$\left ( \frac{2}{p} \right )=(-1)^{n}$ ( Bổ đề Gauss)
$\left ( \frac{2}{p} \right )\equiv 2^{\frac{p-1}{2}}$ (mod p) ( Tiêu chuẩn Euler)
$=>2^{\frac{p-1}{2}}\equiv (-1)^{s}$ (mod p). (Đpcm)

Em muốn anh nêu ra mấy cái chứng minh đó luôn, cho nó dễ hiểu

Có trong sách Tài liệu chuyên toán giải tích 12 đó em. Em tham khảo trong đó

Em muốn anh nêu ra ở đây cho nó dễ nhìn thôi,tiện cho việc hiểu bài   chứ cái này em cx chứng minh một lần trên VMF rồi

Cho $p$ là số nguyên tố lẻ. Gọi n là số các số chẵn nằm trong khoảng $(\frac{p}{2};p)$. Chứng minh rằng:

$$ 2^{\frac{p-1}{2}} \equiv (-1)^n (mod \, p)$$

P/s : Lâu lâu nghịch lại thặng dư cũng hay hay(đùa  )

Chú ý: Không dùng thặng dư bình phương   để giải, hãy nêu một cách giải khác

Anh không hiểu em viết gì, đề bài là nếu tồn tại số nguyên $n$ sao cho $x$ là số chính phương mod $p$ với mọi số nguyên tố $p > n$ thì $x$ phải là một số chính phương.

Cái em đang chứng minh ở đây là $x$ là một số chính phương $mod p$ nếu như $x^{\frac{p-1}{2}} \equiv 1 mod p$ . Còn cái x là số chính phương  thì là phần ở đây :  https://artofproblem...munity/c6h64322

Chứng minh rằng nếu $x^{\frac{p-1}{2}} \equiv 1 \mathbb{mod p}$ từ một lúc nào đó với các số nguyên tố $p$ ( hay nói cách khác là số chính phương $\mathbb{mod p}$ ) thì $x$ là số chính phương 

Đây là lời giải của em: Ta có :$ (x,p)=1$

Xét 2 trường hợp sau:

TH1: $p=2$ , thì x lẻ, Xét số $x=2t+1$ và số $s=2q+1$

Ta có: $s^2-x= (2q+1)^2-(2t+1) =2(2q^2+2q-t) \vdots 2$

Nên $s^2 \equiv x (mod p)$( đpcm)

TH2: $p$ lẻ Ta có:

Với mỗi số $k \in \left \{ 1,2,3,...,p-1 \right \}$ tồn tại duy nhất một số $k' \in \left\{1,2,3,...,p-1 \right \}$ sao cho $kk' \equiv x(mod p)$

Xét 2 trường hợp sau:

$+_{1})$ Nếu $k=k'$ thì $x \equiv k^2$ từ đây suy ra x là số chính phương mod p

$+_{2})$ Nếu với mọi k ta luôn có $ k\neq k'$ , Khi đó tập $\left\{1,2,3,...,p-1 \right \}$ sẽ được chia thành $\frac{p-1}{2}$ tập con $\left \{k;k' \right \}$ sao cho $ kk' \equiv a$

Nên $a^{\frac{p-1}{2}} \equiv (p-1)!$

Theo định lí Wilson , $(p-1)! \equiv -1$

Nên ta có $1 \equiv -1 (mod p)$

Vì p lẻ nên điều này là không thể. Vậy chỉ có $+_{1}$ xảy ra (đpcm)

Nếu em xin lỗi rồi mà người ấy do điêu bẩm sinh ko chịu chấp nhận lời xin lỗ thì sao ạ :v

Livestream nhảy lăm ba đa

Nhưng nếu thành viedn block làm sao trao đổi ạ. Em cảm ơn :v

Nếu block thì m đi xin lỗi người đó rồi livestream nhảy lăm ba đa đi r là họ bỏ block liền

Hay quá ! Có chuyện gì xảy ra vậy!!!????
Các bạn có dự định lập topic ôn hè không? Nếu có mn tham gia vs

Bạn nhầm topic rồi, nếu mà bạn muốn lập topic ôn thì hãy inb trong tin nhắn riêng vs các thành viên

Thôi tha cho cái topic . Có j bàn trên tus ko tội nghiệp nó

ko tính vào số bài viết, nếu mà tính vào số bài viết, thì t đã ko cho bây spam ở đây kkk

Ảnh này lâu rồi . Nó đã đi thì ko về đâu

Nó chơi đồ lề kìa, nhìn cái j ở giữa cổ nó kkkk, chơi trò bác sĩ vs bệnh nhân vs bọn trong NP