Kenji
Thống kê
- Nhóm: Thành viên
- Bài viết: 22
- Lượt xem: 2247
- Danh hiệu: Binh nhất
- Tuổi: Chưa nhập tuổi
- Ngày sinh: Chưa nhập ngày sinh
-
Giới tính
 Bí mật
Bí mật
1
Trung bình
Công cụ người dùng
Bạn bè
Kenji Chưa có ai trong danh sách bạn bè.
Lần ghé thăm cuối
Trong chủ đề: RUBIC - NHỮNG AI QUAN TÂM !
05-10-2009 - 19:03
Nhìn theo gốc độ toán học mà nói, thì có tồn tại một phép quay tuần hoàn nào đó để sau hữu hạn phép quay thì từ bất cứ trạng thái nảo của khối Rubic ta đều nhận được trang thái hoàn hảo - tức các mặt có cùng một màu, không? Theo tôi, bằng toán học, điều đó "có thể" là có! các pác nghĩ sao?
Trong chủ đề: bài hình khá dễ
27-03-2007 - 08:16
Có một BDT liên quan đến cái DT này:
4R+r $sqrt{3} p$
$sqrt{3} p$
4R+r
Trong chủ đề: $\sum\left\lfloor\dfrac{(q-1)p}{q}\right...
03-03-2007 - 11:50
Tuy nhiên vấn đề vẫn chưa được giải quyết trọn vẹn! Đó chỉ là một bước nhỏ trong bài toán:
Tìm số n nguyên dương để $A = 7^{n} + 21^{n}$ là một số chính phương. Hiển nhiên công đoạn nhỏ ở trên chỉ nằm trong cách giải của tôi. Còn bây giờ thì mời các bạn giải bài toán trên theo cách của riêng mình(Và post lên cho mọi người cùng tham khảo)
Tìm số n nguyên dương để $A = 7^{n} + 21^{n}$ là một số chính phương. Hiển nhiên công đoạn nhỏ ở trên chỉ nằm trong cách giải của tôi. Còn bây giờ thì mời các bạn giải bài toán trên theo cách của riêng mình(Và post lên cho mọi người cùng tham khảo)
Trong chủ đề: $\sum\left\lfloor\dfrac{(q-1)p}{q}\right...
03-03-2007 - 11:41
Ah! Cảm ơn ông bạn fecma21 rất nhiều, công thức nghiệm như sau:
$ r_{0}=1; r_{1}=55; r_{n+2}=110.r_{n+1} - r_{n}$
$m_{0}=0; m_{1}=6; m_{n+2}=110.m_{n+1} - m_{n}$, n=0,1,2,3,...
$ r_{0}=1; r_{1}=55; r_{n+2}=110.r_{n+1} - r_{n}$
$m_{0}=0; m_{1}=6; m_{n+2}=110.m_{n+1} - m_{n}$, n=0,1,2,3,...
Trong chủ đề: $\sum\left\lfloor\dfrac{(q-1)p}{q}\right...
28-02-2007 - 11:33
Ah! Cảm ơn Supermember nhiều hén, k phải là số nguyên $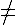 $2
$2
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Bài viết: Kenji


 Tìm kiếm
Tìm kiếm

