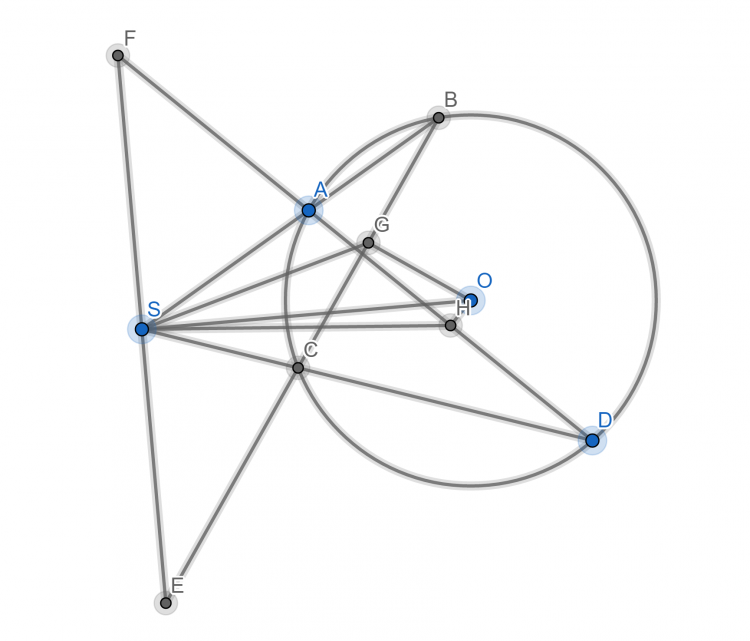
Vẽ OG vuông góc với BC và OH vuông góc với AD.
Ta có: $\Delta SAD$ đồng dạng với $\Delta SCB$ (g.g). Mà G, H lần lượt là trung điểm của BC và AD. $\Rightarrow \Delta SAH$ đồng dạng với $\Delta SCG$ (c.g.c).
$\Rightarrow \angle SHA = \angle SGC \Leftrightarrow \angle SHF = \angle SGE$ (1)
FSHO và ESGO là các tứ giác nội tiếp (do $\angle OSF=\angle OHF=\angle OGE=\angle OSE=90^{o}$) $\Rightarrow \left\{\begin{matrix} \angle SHF=\angle SOF\\ \angle SGE=\angle SOE\end{matrix}\right.$ (2).
Từ (1) và (2) suy ra $\angle SOF=\angle SOE$. Mà OS là đường cao tam giác OFE nên tam giác OFE cân tại O $\Rightarrow OE=OF$
- Khoa Linh, buingoctu, conankun và 1 người khác yêu thích


 Tìm kiếm
Tìm kiếm Bí mật
Bí mật