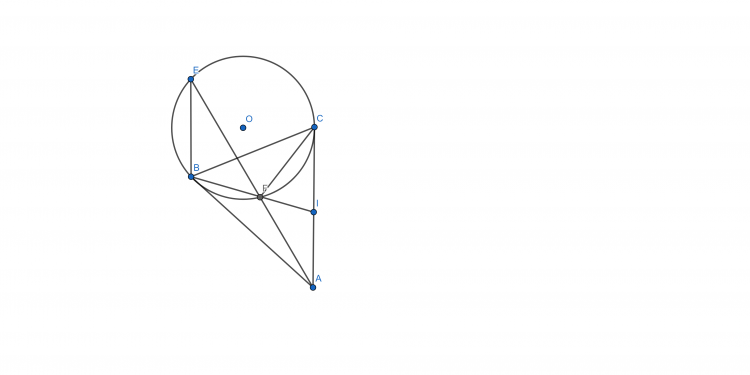
Bài 1 ( làm theo kiến thức lớp 8)
Ta có: $(a-b+c)^{2}=a^{2}+b^{2}+c^{2}-2ab+2ac-2bc\geqslant 0$
$\Rightarrow a^{2}+b^{2}+c^{2}\geqslant 2ab-2ac+2bc$ (1)
Mặt khác ta có: $b^{2}+bc+c^{2}=b^{2}+2.b.\frac{c}{2}+\frac{c^{2}}{4}+c^{2}-\frac{c^{2}}{4}=\left ( b+\frac{c}{2} \right )^{2}+\frac{3c^{2}}{4}\geqslant 0$
$\Rightarrow b^{2}+c^{2}\geqslant -bc$ (2)
Lấy (1) + (2) vế theo vế ta được : $a^{2}+2b^{2}+2c^{2}\geqslant 2ab-2ac+bc$ (đpcm)
- dchynh yêu thích


 Tìm kiếm
Tìm kiếm Nam
Nam