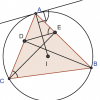
$ \textbf{Bài toán} $ Cho $ \Delta ABC $ nội tiếp $ (O) $ có phân giác $ AD $ cắt $ (O) $ tại $ D $. Gọi $ M $ là 1 điểm bất kì trên $ AD $, $ BM, CM $ cắt $ (O) $ tại $ E, F $. $ EF $ cắt tiếp tuyến của $ (O) $ tại $A$ ở $ T $.
CMR: $ TM // BC $.
- Arthur Pendragon yêu thích



 Tìm kiếm
Tìm kiếm Không khai báo
Không khai báo











 Gửi bởi
Gửi bởi 

