Lời giải của mình:
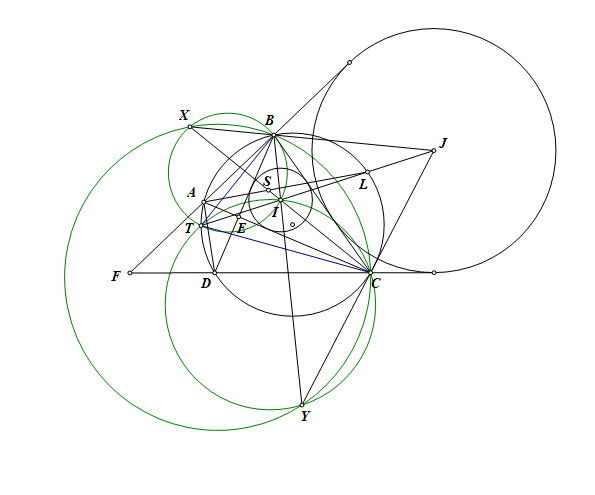
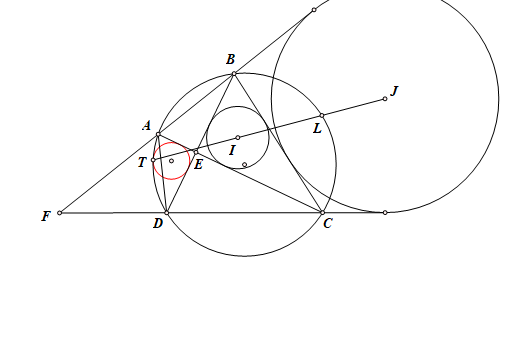
Gọi $E$ là giao điểm của $AC$ và $BD$. $F$ là giao điểm của $AB$ và $CD$.
Gọi $L$ là điểm chính giữa cung $BC$ không chứa $A,D$, $LI$ cắt $(O)$ lần thứ hai tại $T$.
Gọi $X,Y$ lần lượt là tâm các đường tròn bàng tiếp góc $C,B$ của $\triangle ABC, \triangle BDC$
Nếu gọi $S$ là tâm đường tròn nội tiếp tam giác $ABC$ thì ta có $\angle XBS = \angle XAS = 90^0 \Rightarrow XBSA$ nội tiếp
$\Rightarrow \angle BXI = \angle BAS = \angle BTI \Rightarrow$ Tứ giác $XBIT$ nội tiếp.
Tương tự ta cũng chứng minh được tứ giác $TICY$ nội tiếp.
Từ đó ta có $\angle BXC = \angle BTL = \angle CTL = \angle BYC \Rightarrow XBCY$ nội tiếp.
Do $XB, BJ$ đều là phân giác ngoài góc $ABC$ nên $X,B,J$ thẳng hàng. Tương tự, $Y,C,J$ thẳng hàng.
Theo tính chất trục đẳng phương thì trục đẳng phương của ba đường tròn xanh phải đồng quy, tức là $XB, TI, YC$ đồng quy. Mà $XB$ cắt $YC$ tại $J$, suy ra $T,I,J$ thẳng thàng.
Do đó $I,J,L$ thẳng hàng hay ta có $đpcm \blacksquare$
P/S: Nếu ta dựng một đường tròn $\omega$ tiếp xúc với $AE, DE$ và tiếp xúc trong với $(O)$ thì $T$ là tiếp điểm của $\omega$ với $(O)$
- DaiphongLT yêu thích


 Tìm kiếm
Tìm kiếm Nam
Nam








 Gửi bởi
Gửi bởi