Tìm kiếm
Nam
$a\sqrt{b-1}+b\sqrt{a-1}\leq \frac{a}{2}.(b-1+1)+\frac{b}{2}(a-1+1)=ab$
dongvmf10
#724528 Cho a,b ≥ 1. chứng minh rằng: a căn ( b-1) + b căn( a-1) ≤ ab
Gửi bởi
trong 06-08-2019 - 22:33
#723094 Chứng minh rằng HC=HK
Gửi bởi
trong 16-06-2019 - 21:46
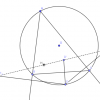
Cho tứ giác điều hòa ABCD nội tiếp (O);M là giao điểm hai tiếp tuyến tại B,D của (O).Đường thẳng song song với AB kẻ qua C cắt DB,DA lần lượt ở H,K.Chứng minh rằng HC=HK.
Tiện thể ai có tài liệu chứng minh các tính chất với một số bài toán cơ bản của tứ giác điều hòa không ạ?
- tritanngo99 yêu thích
#722618 $$\sum\limits_{cyc}\frac{y}...
Gửi bởi
trong 29-05-2019 - 22:32
Mình làm thử , ko biết có đúng ko
\[\\\sum \frac{y}{\sqrt{2z(x+y)}}\geq \sum \frac{2y}{x+y+2z}=\sum \frac{2y^{2}}{xy+y^{2}+2yz} \\\geq\frac{2.(x+y+z)^2}{(x+y+z)^{2}+xy+yz+xz}\geq \frac{2.(x+y+z)^2}{(x+y+z)^{2}+\frac{(x+y+z)^{2}}{3}}=\frac{3}{2}\]
- DOTOANNANG yêu thích
#722617 Tính A = $\frac{1}{2!}$ + $\...
Gửi bởi
trong 29-05-2019 - 21:48
Ta có: $\frac{n}{(n+1)!}=\frac{n+1}{(n+1)!}-\frac{1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!}$
Bạn thay vào biểu thức và thu gọn đi là được.
- Nam Rom và nguyendinhnguyentoan9 thích
#722563 Tìm giá trị nhỏ nhất $P=(a^{2}+b^{2}+c^{2}...
Gửi bởi
trong 27-05-2019 - 22:28
Cho ba số thực a,b,c thỏa mãn $a^{3}+b^{3}+c^{3}=3abc+32$.Tìm giá trị nhỏ nhất của biểu thức
$P=(a^{2}+b^{2}+c^{2})(\left | a-b \right |+\left | b-c \right |+\left | c-a \right |)$
- tritanngo99 yêu thích
#722467 Chứng minh rằng $(\frac{4}{a^2+b^2}+1)(\fr...
Gửi bởi
trong 25-05-2019 - 09:00
Cho $a,b,c>0$ thỏa mãn : $a^{2}+b^{2}+c^{2}=3$
.Chứng minh rằng: $(\frac{4}{a^2+b^2}+1)(\frac{4}{b^2+c^{2}}+1)(\frac{4}{a^2+c^2}+1)\geq 3(a+b+c)^{2}$
- tritanngo99, Tea Coffee và phongmaths thích
