KietLW9

Một bài hình hay mình vừa lụm được trên facebook

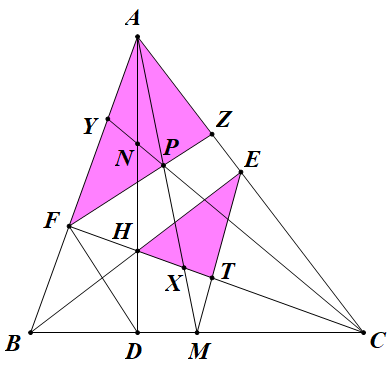
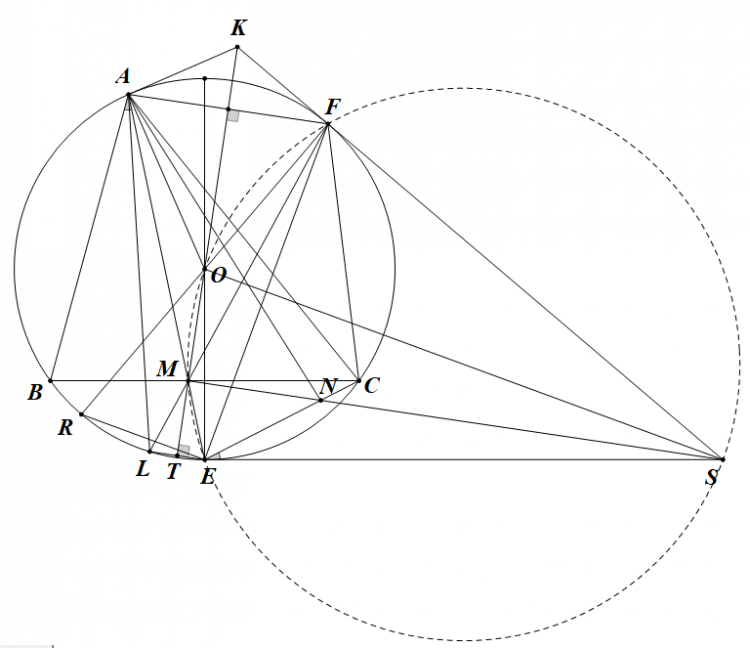
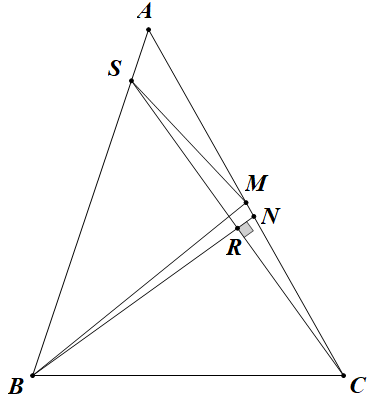
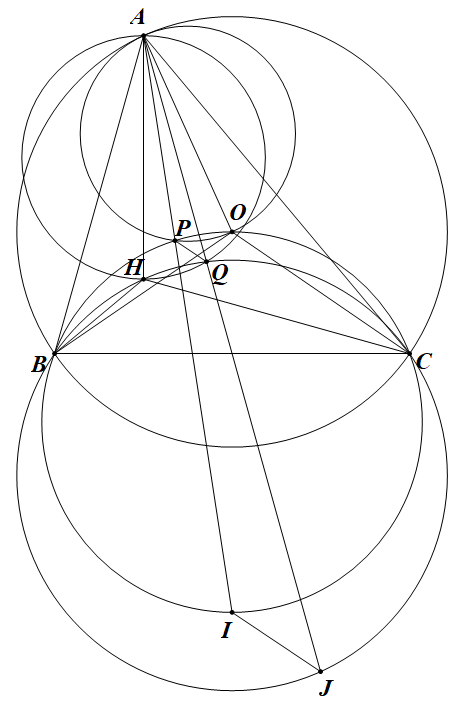
Bài 14: Cho $\Delta ABC$ có ba đường cao $AD,BE,CF$ đồng quy tại $H$. $M,N$ là trung điểm của $BC,AH$. Gọi $P$ là giao điểm của $AM$ và $CN$. Chứng minh: $\angle PFD=90^{\circ}$

Lời giải.

Gọi $X$ là giao điểm của $CF$ và $AM$, $Y$ là giao điểm của $CN$ và $AB$, $Z$ là giao điểm của đường vuông góc với $FD$ tại $F$ và $AC$, $T$ là giao điểm của $FC$ và $EM$.

Ta cần chứng minh $AX,FZ,CY$ đồng quy nữa là xong

Thật vậy, xét các cặp tam giác đồng dạng ta suy ra các cặp cạnh tỉ lệ theo thứ tự: $\Delta HTE \sim \Delta AZF,\Delta CHE \sim \Delta CAF,\Delta CTE \sim \Delta CZF\Rightarrow \frac{HT}{AZ}=\frac{HE}{AF}=\frac{CE}{CF}=\frac{CT}{CZ}$

$\Rightarrow \frac{TH}{TC}=\frac{AZ}{CZ}$

Áp dụng định lý Menelaus trong $\Delta BHC$ với bộ ba điểm $M,T,E$ thẳng hàng, ta được: $\frac{MB}{MC}.\frac{TC}{TH}.\frac{EH}{EB}=1\Rightarrow \frac{TH}{TC}=\frac{EH}{EB}$

Vậy ta có được: $\frac{ZA}{ZC}=\frac{EH}{EB}$ 

Tiếp tục áp dụng định lý Menelaus cho $\Delta BFC$ với bộ ba điểm $M,X,A$ thẳng hàng, ta được: $\frac{MB}{MC}.\frac{XC}{XF}.\frac{AF}{AB}=1\Rightarrow \frac{XC}{XF}=\frac{AB}{AF}$

Áp dụng định lý Menelaus cho $\Delta AFH$ với bộ ba điểm $Y,N,C$ thẳng hàng, ta được: $\frac{NA}{NH}.\frac{CH}{CF}.\frac{YF}{YA}=1\Rightarrow \frac{YF}{YA}=\frac{CF}{CH}$

Tổng hợp các tỉ số trên, ta được: $\frac{ZA}{ZC}.\frac{XC}{XF}.\frac{YF}{YA}=\frac{EH}{EB}.\frac{AB}{AF}.\frac{CF}{CH}=\frac{EH.CF}{CH.BE}.\frac{AB}{AF}=\frac{FH.CF}{BH.BE}.\frac{AB}{AF}=\frac{BF.FA}{BF.AB}.\frac{AB}{AF}=1$

Theo Menelaus đảo thì ta có $AX,FY,CZ$ đồng quy. Vậy ta có điều phải chứng minh.

Bổ đề: Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O)$. $M,N$ là điểm chính giữa cung nhỏ, lớn $BC$. Điểm $P$ thuộc $HM$ sao cho $OP//AM$. $Q$ là điểm đối xứng với $N$ qua $BC$ thì $P,Q$ liên hợp đẳng giác trong $\Delta ABC$.

Chứng minh:

Gọi $Z$ là giao điểm hai tiếp tuyến tại $B,C$ của đường tròn $(O)$, $J$ là chân đường cao hạ từ $A$ xuống $BC$, $T$ là giao điểm của $OC$ và $AM$, $AD$ là đường kính của $(O)$.

Ta cần chứng minh: $\angle OPZ=90^{\circ}$

Ta có: $\angle AMD=90^{\circ}$ mà $OP//AM$ nên $OP$ vuông góc với $MD$ tại $G$

Dễ có rằng $AH=2OL$ và $\Delta AHM\sim\Delta OMP(g.g)\Rightarrow OP=\frac{OM.AM}{AH}=\frac{OZ.OG}{OM}$ (Do $OM^2.AM=OB^2.AM=OL.OZ.AM=\frac{AH}{2}.OZ.2OG=AH.OZ.OG$)

$\Rightarrow \frac{OM}{OZ}=\frac{OG}{OP}\Rightarrow MG//ZP$ nên $\angle OPZ=90^{\circ}$

Vậy ta có $P$ thuộc $(BOC)$

$\Rightarrow \angle PBC+\angle QBA=\angle POC+\angle ABC+\angle QBC=\angle MTC+\angle ABC+\angle QBC=180^{\circ}-\angle TMC-\angle TCM+\angle ABC+\angle QBC=180^{\circ}-\angle ABC-\angle NBC+\angle ABC+\angle QBC=180^{\circ}$

Tương tự thì: $\angle PCB+\angle QCB=180^{\circ}$ nên $P,Q$ liên hợp đẳng giác trong $\Delta ABC$

Vậy bổ đề được chứng minh.

Quay lại bài toán

Gọi $L$ là điểm chính giữa cung lớn $BC$ và $Q$ đối xứng với $L$ qua $BC$ thì theo bổ đề: $P,Q$ liên hợp đẳng giác trong $\Delta ABC$. Từ $Q$ kẻ $QW,QS,QR$ vuông góc với $BC,CA,AB$

Vì $P, Q$ liên hợp đẳng giác nên sáu điểm $X,Y,Z,W,R,S$ đồng viên

Ta có: $MQ=WQ-MW=LW-WM=LM-2MW=2OM-2WM=2OW=AH$ kết hợp với $AH//MQ$ suy ra $AHQM$ là hình bình hành nên nếu gọi $I$ là trung điểm của $HM$ thì $I$ cũng là trung điểm của $AQ$

Hay nói cách khác ta cần chứng minh $R,I,W,S$ đồng viên

Thật vậy, sử dụng các tứ giác nội tiếp $BWQR,QWCS$ ta có: $\angle RWS=\angle RWQ+\angle SWQ=\angle RBQ+\angle SCQ=180^{\circ}-\angle RQB-\angle SQC=180^{\circ}-(180^{\circ}-\angle BQC-\angle BAC)=2\angle BAC$

và $\angle RIS=2\angle RAI+2\angle SAI=2\angle BAC$

Bài toán được chứng minh hoàn toàn.

Đặt $(\frac{1}{x^2},\frac{1}{y^2},\frac{1}{z^2})\rightarrow (a,b,c)$ thì $a+b+c=3$

và $\frac{1}{\sqrt{x^6+y^2}}=\frac{1}{\sqrt{\frac{1}{a^3}+\frac{1}{b}}}=\frac{\sqrt{a^3b}}{\sqrt{a^3+b}}\leqslant \frac{\sqrt[4]{a^6b^2}}{\sqrt{2\sqrt{a^3b}}}=\frac{\sqrt[4]{a^3b}}{\sqrt{2}}\leqslant \frac{3a+b}{4\sqrt{2}}$

Tương tự rồi cộng lại, ta có điều phải chứng minh

hình.png

Gọi $J,K$ lần lượt là hình chiếu của $I$ trên $AB,AC$.

Khi đó $J,K$ lần lượt là trung điểm của $EF,GH$.

Ta có $AE+AF=2AJ;AH+AG=2AK$ nên ta quy về chứng minh $BD-CD=2(AK-AJ)$.

Ta có $BD-CD=\frac{BD^2-CD^2}{BD+CD}=\frac{BI^2-CI^2}{BC}=\frac{(BJ^2-CK^2)+(IJ^2-IK^2)}{BC}=\frac{(BJ-CK)(BJ+CK)+(AK^2-AJ^2)}{BC}=\frac{(AK-AJ)(BJ+CK)+(AK-AJ)(AK+AJ)}{BC}=\frac{(AK-AJ)(AB+AC)}{BC}=2(AK-AJ)$ hay ta có đpcm.

Biến đổi cạnh khá hay nhưng có thể vẽ song song như hình bên dưới

Bài tiếp theo

Bài 13: Cho tứ giác $ABCD$ nội tiếp $(O)$. $E$ là giao của $AD$ và $BC$. $EF$ là đường kính của $(ECD)$. $Q$ là điểm chính giữa cung lớn $CD$ của $(ECD)$. $QF$ cắt $CD,AC$ tại $H,G$. $P$ là điểm chính giữa cung nhỏ $CD$ của $(ECD)$. $PF$ cắt $BD,CD$ tại $K,L$. Chứng minh $(DKL)$ tiếp xúc $(CGH)$

Vì $M$ là trung điểm của $BC$ nên $\angle GMO=\angle GPO=90^{\circ}$ 

Mà $GP//KJ$ nên $PO$ vuông góc $KJ$ mà $OK=OJ$ nên $PO$ là đường trung trực của $KJ$ nên $PK=PJ$

Vậy ta có được: $PK=PJ=PL$ nên $\Delta KJL$ vuông tại $J$

Suy ra $PO//JL$ (cùng vuông góc với $KJ$)

Từ đây suy ra $GP$ vuông góc $LJ$ mà $PL=PJ$ nên $GL=GJ$

Tiếp theo là một bài giải trí vui vui, nhưng cũng khá hay!

Bài 11: Cho hình vẽ. Biết tam giác $ABC$ đều và đường tròn $(I)$ tiếp xúc với $BC$ như hình. Chứng minh: $BD+AE+AF=CD+AG+AH$

Bài 10: Cho dây cung $BC$ trên $(O)$. $A$ di chuyển trên cung lớn $BC$. $E,F$ đối xứng với $B,C$ qua $AC,AB$. $I$ là trung điểm của $EF$. Chứng minh $AI$ đi qua một điểm cố định

Đây là một bổ đề khá lạ mình chưa gặp và nó khá chặt   

Ta cần chứng minh: $(ab+bc+ca)(ab^2+bc^2+ca^2)^2\geqslant 9a^2b^2c^2(a^2+b^2+c^2)$

$\Leftrightarrow (a^5bc^2+b^5ca^2+c^5ab^2)+(a^5c^3+b^5a^3+c^5b^3)+(2a^4b^3c+2b^4c^3a+2c^4a^3b)+(a^4bc^3+b^4ca^3+c^4ab^3)+(2a^3b^2c^3+2b^3c^2a^3+2c^3a^2b^3)\geqslant 7a^4b^2c^2+7b^4c^2a^2+7c^4a^2b^2$

Theo AM-GM: $a^5bc^2+a^5c^3+2a^4b^3c+a^4bc^3+2a^3b^3c^2=a^5bc^2+a^5c^3+a^4b^3c+a^4b^3c+a^4bc^3+a^3b^3c^2+a^3b^3c^2\geqslant 7\sqrt[7]{a^{28}b^{14}c^{14}}=7a^4b^2c^2$

Tương tự rồi cộng lại, ta có điều phải chứng minh

Lời giải.

Ta có: $a(b^2+10)(c^2+10)+b(c^2+10)(a^2+10)+c(a^2+10)(b^2+10)=abc(ab+bc+ca)+10(a^2b+ab^2+b^2c+bc^2+c^2a+ca^2)+100(a+b+c)=3abc-30abc+10(a+b+c)(ab+bc+ca)+100(a+b+c)=130(a+b+c)-27abc$

và $(a^2+10)(b^2+10)(c^2+10)=a^2b^2c^2+10(a^2b^2+b^2c^2+c^2a^2)+100(a^2+b^2+c^2)+1000=\left [ 100(a+b+c)^2-20abc(a+b+c)+a^2b^2c^2 \right ]+10\left [ (ab+bc+ca)^2-20(ab+bc+ca)+100 \right ]=\left [ 10(a+b+c)-abc \right ]^2+10(ab+bc+ca-10)^2=\left [ 10(a+b+c)-abc \right ]^2+490$

Đặt $a+b+c=p;ab+bc+ca=q=3;abc=r$ thì ta cần chứng minh: $\frac{130p-27r}{(10p-r)^2+490}\leqslant \frac{3}{11}$

Áp dụng AM-GM, ta được: $(10p-r)^2+841\geqslant 58(10p-r)\Rightarrow (10p-r)^2+490\geqslant 580p-58r-351$

Đến đây ta cần chứng minh: $\frac{130p-27r}{580p-58r-351}\leqslant \frac{3}{11}\Leftrightarrow 310p+123r-1053\geqslant 0$

+) Nếu $p\geqslant 2\sqrt{3}$ thì bất đẳng thức hiển nhiên

+) Nếu $3\leqslant p\leqslant 2\sqrt{3}$ thì áp dụng Schur, ta có: $310p+123r-1053\geqslant 310p+\frac{123p(4q-p^2)}{9}-1053=310p+\frac{41p(12-p^2)}{3}-1053$

Cần có: $310p+\frac{41p(12-p^2)}{3}-1053\geqslant 0\Leftrightarrow (3-p)(41p^2+123p-1053)\geqslant 0$ (Đúng với mọi $p$ thuộc khoảng đang xét)

Đẳng thức xảy ra khi $a=b=c=1$

Bài 10: Cho tam giác $ABC (AB < AC)$ nội tiếp $(O)$. Tia phân giác trong $AM$ của tam giác $ABC$ cắt $(O)$ tại điểm $E$ khác $A$. Gọi $d$ là đường thẳng qua $A$ và vuông góc $OM$. Gọi $F$ là giao điểm khác $A$ của $(O)$ và $d$. Tiếp tuyến của $(O)$ tại $E$ và $F$ cắt nhau tại $S$. Gọi giao điểm của $EC$ và $MS$ là $N$, $L$ là giao điểm khác $A$ của $AN$ và $(O)$. Chứng minh rằng $OM$ vuông góc với $MN$.

Gọi giao điểm của $FM$ với $(O)$ là $L$, kẻ đường kính $FR$

Dễ thấy $MO$ là trục đối xứng của hình thang $ALEF$ nên $MO$ vuông góc $LE$ tại $T$

Ta có: $\angle TME=90^{\circ}-\angle AEL=90^{\circ}-\angle FRE=\angle RFE$ nên tứ giác $EMOF$ nội tiếp mà tứ giác $EOFS$ nội tiếp nên 5 điểm $E,M,O,F,S$ đồng viên

Vậy ta có điều phải chứng minh

Áp dụng AM-GM, ta có: 

$(ab+cd)(ac+bd)\leqslant \frac{(ab+cd+ac+bd)^2}{4}=\frac{(a+d)^2(b+c)^2}{4}\leqslant \frac{\left [ \frac{(a+b+c+d)^2}{4} \right ]^2}{4}=4$

$(ad+bc)(bd+ac)\leqslant \frac{(ad+bc+bd+ac)^2}{4}=\frac{(a+b)^2(c+d)^2}{4}\leqslant \frac{\left [  \frac{(a+b+c+d)^2 }{4}\right ]^2}{4}=4$

Lại có:

$a^2bc+b^2cd+c^2da+d^2ab-(ab+cd)(ac+bd)=bd(c-a)(b-d)$

$a^2bc+b^2cd+c^2da+d^2ab-(ad+bc)(bd+ac)=ac(a-c)(b-d)$

Vậy $a^2bc+b^2cd+c^2da+d^2ab\leqslant max\left \{ (ab+cd)(ac+bd),(ad+bc)(bd+ac) \right \}\leqslant 4$

 

Bài 9: Một bài mình được thầy ra năm trước và mình tìm ra cách kẻ phụ khá hay:

Cho $\Delta ABC$ thoả mãn $AB-BC=\frac{AC}{\sqrt{2}}$ có $M$ là trung điểm của $AC$, $BN$ là phân giác trong. Chứng minh rằng $\widehat{BMC}+\widehat{BNC}=90^\circ$.

 

Từ giả thiết ta có $AB>BC$ nên $N$ nằm giữa $M$ và $C$. Kẻ $CR$ vuông góc $BN$, $CR$ cắt $AB$ tại $S$ thì $S$ nằm giữa $A$ và $B$ do $BC=BS<AB$

Vì $BC=BS$ nên $AB-BC=AS=\frac{AC}{\sqrt{2}}\Rightarrow AS^2=\frac{AC^2}{2}=AC.AM\Rightarrow \Delta ASM\sim\Delta ACS(c.g.c)\Rightarrow \angle ASM=\angle ACS$

$BM$ là trung tuyến của tam giác $ABC$ nên $BM^2=\frac{2(AB^2+BC^2)-AC^2}{4}=\frac{2AB^2+2BC^2-2(AB-BC)^2}{4}=AB.BC=BS.AB\Rightarrow \Delta BMS\sim\Delta BAM\Rightarrow \angle BMA=\angle BSM\Rightarrow \angle BMC=\angle ASM$

Vậy ta có: $\angle BMC=\angle ACS\Rightarrow \angle BMC+\angle BNC=\angle ACS+\angle RNC=90^{\circ}$

Gợi ý các bạn là dùng Schur

Cho $a,b,c>0$ và $ab+bc+ca=3$

Chứng minh rằng: $\frac{a}{a^2+10}+\frac{b}{b^2+10}+\frac{c}{c^2+10}\leqslant \frac{3}{11}$

Một bài rất hay!

Bài đầu tiên trong năm 2022 

Bài 8: Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ có trực tâm $H$. $(BOC)$ cắt đường tròn đường kính $AO$ tại $P$, $(BHC)$ cắt đường tròn đường kính $AH$ ở $Q$. $AP$ cắt $(BOC)$ ở $I$, $AQ$ cắt $(BHC)$ ở $J$. Chứng minh $PQ//IJ$