DaiphongLT

bạn chỉ rõ hơn cách cm bổ đề đc ko

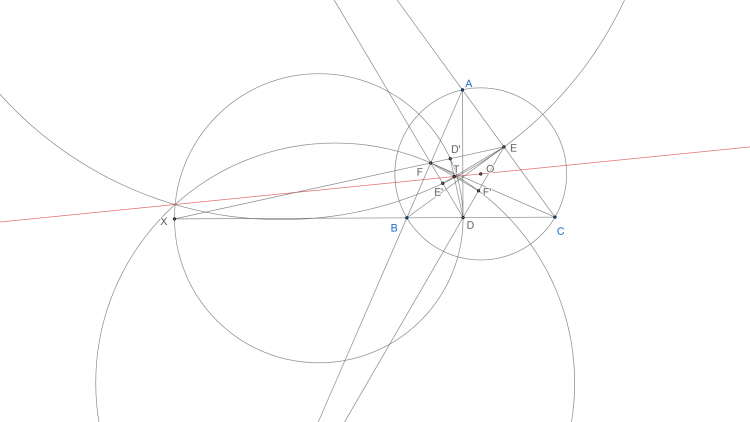
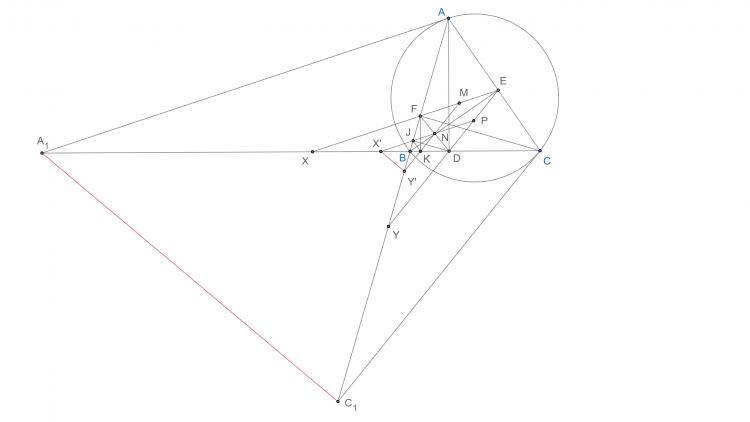
Bổ đề 1: Gọi $AI$ cắt $BC, EF$ tại $D$, $K$. $EF$ cắt $AT, BC$ tại $S, L$. Khi đó ta có $SA=SK=SL$.
Menelaus cho $\Delta ATD$ với cát tuyến $L, S, K$. Chú ý $(AI,KD)=-1$. Biến đổi tỉ số để suy ra được $TI//EF$ và $TA=TI$.
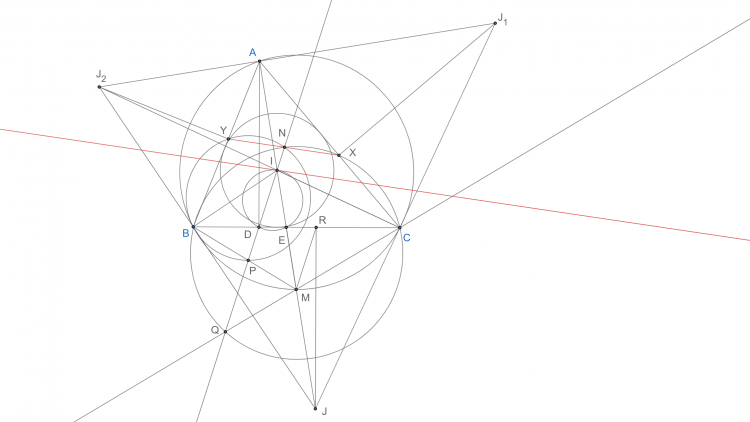
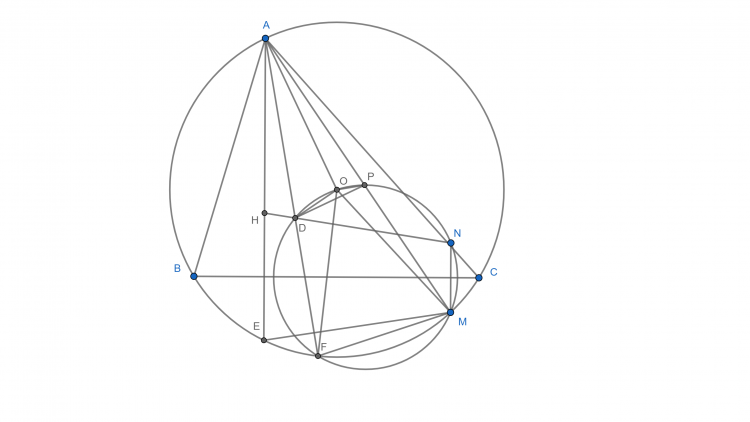
Bổ đề 2: Gọi giao 2 tiếp tuyến tại $B, C$ của $(O)$ là $D$. $ID$ cắt $EF$ tại $M$. $\frac{MF}{ME}=\frac{sin\widehat{MIF}}{sin\widehat{MIE}}.\frac{IF}{IE}=\frac{sin\widehat{DIC}}{sin\widehat{DIB}}.\frac{sin\widehat{FAI}.AI}{\widehat{AFC}}.\frac{sin\widehat{AEB}}{AI.\widehat{sinEAI}}=\frac{sin\widehat{DIC}}{sin\widehat{DIB}}.\frac{sin\widehat{IBD}}{sin\widehat{ICD}}=1$.               
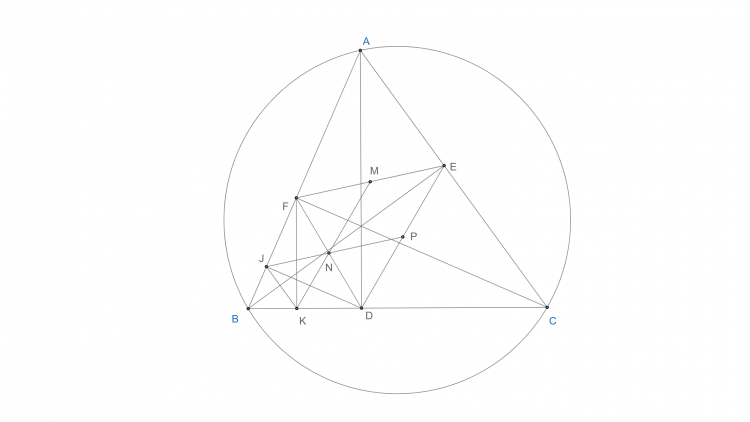
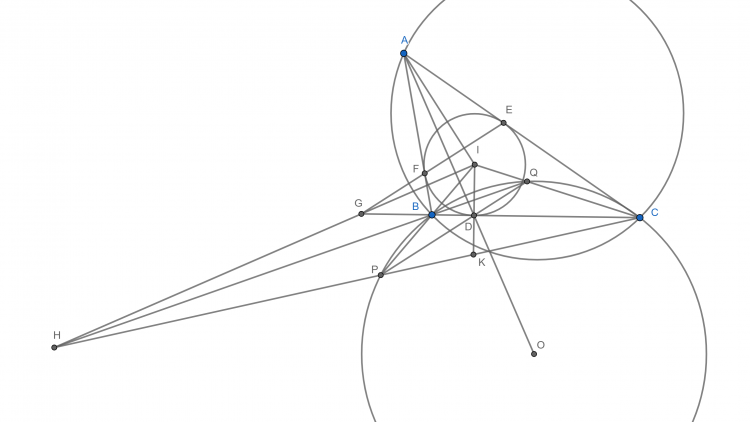
@chỉ đơn giản là biến đổi góc, gọi $IG$ cắt $(AEF)$ tại $Z$, biến đổi góc để dc $\widehat{IAZ} = 90^{\circ}$. Chú ý $T$ là tâm $(AGI)$                  

Cho tam giác $ABC$ nội tiếp $(O)$. $E,F$ lần lượt trung điểm cung nhỏ và cung lớn $BC$. Gọi $I$ là trung điểm $AE$. $K$ là hình chiếu của $F$ lên $AC$. Chứng minh tứ giác $AKIB$ nội tiếp.

Gợi ý: - Gọi $M$ trung điểm $BC$. Chứng minh $\Delta EBT\sim \Delta CBK$ thông qua đồng dạng tương ứng ($M$ trung điểm $BC$ và $T$ trung điểm $AE$)
 

Cho $\Delta ABC$ nội tiếp $(O)$ trong đó $B,C$ cố định , $A$ thay đổi trên cung lớn $BC$ , I là tâm nội tiếp $\Delta ABC$

Đường tròn $Mix-A$ tiếp xúc $AB,AC$ lần lượt tại $E,F$ và tiếp xúc với $(O)$ tại $K$ . Đường thẳng qua $E$ và vuông góc với $IB$ cắt đường thẳng qua $F$ vuông góc với $IC$ tại $P$. Chứng minh rằng $IP$ đi qua điểm cố địng khi A di động 

Gợi ý: - $M, N$ là điểm chính giữa cung $BC$ lớn, nhỏ của $(O)$. Chứng minh $K, P, N$ thẳng hàng
           - Điểm cố định là điểm đối xứng với $M$ qua $N$ (dùng bổ đề hình thang). Chú ý tâm đường tròn $A-Mix$ nằm trên $AN$ và $K, I, M$ thẳng hàng

Cho tam giác nhọn A1B1C1. Trên các cạnh B1C1,C1A1,A1B1 lần lượt lấy A,B,C sao cho $\triangle ABC\sim \triangle A1B1C1$.CMR các trực tâm của tam giác ABC và A1B1C1 cách đều tâm đường tròn ngoại tiếp tam giác ABC

Gợi ý: - Gọi $O$ là tâm ngoại tiếp $\Delta ABC$ thì $O$ cũng là trực tâm $\Delta A_1B_1C_1$. Khi đó $O$ là điểm Miquel của bộ điểm $A_1, B_1, C_1$ trong $\Delta ABC$
           - $H$ là trực tâm $\Delta ABC$, $O'$ là tâm ngoại tiếp $\Delta A_1B_1C_1$
           - $AH$ cắt $(AB_1C_1)$ tại $D$. Chứng minh $O'$ là tâm $(DHO)$. Chú ý $\Delta AHO\sim \Delta A_1OO'$
@mình đã sữa, cảm ơn Explorer

Cho tam giác ABC nội tiếp (O) với I là tâm nội tiếp. BI cắt AC tại E. CI cắt AB tại F. (AEF) cắt (O) tại P. và L là điểm chính giữa cung lớn BC của (O). CM PL cắt BC tại điểm nằm trên trung trực của AI

Gợi ý: Dùng 2 bổ đề sau
Bổ đề 1: Tiếp tuyến tại $A$ của $(AEF)$ cắt $BC$ tại $T$. Khi đó $T$ thuộc trung trực $AI$ và $TI//EF$
Bổ đề 2: $D$ là giao điểm hai tiếp tuyến tại $B$ và $C$ của $(O)$. Khi đó $ID$ đi qua trung điểm $EF$
Sau đó gọi $ID$ cắt $BC$ tại $S$, $LS$ cắt $(O)$ tại $X$. Chứng minh $(GX, BC)=-1$. Sau đó dùng bổ đề 1 là xong            
                         

$a)$ Gọi $X$ là giao hai tiếp tuyến tại $B, C$ của $(O)$. Tâm $(AEF)$ chính là trung điểm $AX$. Dùng phương tích để chứng minh $O'X=const$ với $O'$ là tâm $(BOC)$
$b)$ $Q$ là điểm thuộc $(O)$ sao cho $AQ//BC$
$c)$ Gọi $T$ là hình chiếu của $A$ lên $BC$ thì $G$ và $T$ đối xứng với nhau qua $D$ (Iran TST 2015). Khi đó có $A(QD, TG)=-1$ là xong           

Bài toán 23. Cho tam giác $ABC$ nhọn với đường cao $AD,BE,CF$ đồng quy tại $H$. $M$ là trung điểm $BC$. Trên $EF$ lấy các điểm $Q,R$ sao cho $MQ⊥AB$ và $MR⊥AC$. Lấy các điểm $S,T$ sao cho $CS||RT⊥DE$, $QS||BT⊥DF$. $K$ là hình chiếu của trung điểm $AH$ lên $HM$. Chứng minh $DK⊥ST$

Gọi $QB$ cắt $CR$ tại $X$, dễ thấy $QB, CR$ lần lượt là tiếp tuyến của đường tròn $(O)$ nên $\widehat{SQB}= \widehat{TRC}=90^{\circ} \Rightarrow$ $SQXC, TRXB$ nội tiếp
Gọi $AH$ và $MH$ cắt $(O)$ tại $I$ và $G$ như hình vẽ. Khi đó $K$ là trung điểm $GH$
Gọi $J$ là giao điểm thứ hai của $(XQC)$ và $(XBR)$ $\Rightarrow$ $\Delta JQB\sim \Delta JCR(g-g)\Rightarrow \frac{JQ}{JC}=\frac{QB}{CR}$
Biến đổi góc đơn giản dễ thấy $G, Q, B, M, E$ nên $\Delta GQB\sim \Delta GFH(g-g)\Rightarrow \frac{GQ}{QB}=\frac{GF}{FH}$
Tương tự $G, R, C, M, F$ đồng viên nên $\Delta GRC\sim \Delta GEH(g-g)\Rightarrow \frac{GR}{CR}=\frac{GE}{EH}$. Mà $(GH, FE)=-1$ nên $\frac{GF}{FH}=\frac{GE}{EH}$ nên $\frac{GQ}{QB}=\frac{GR}{CR}$$\Leftrightarrow \frac{GQ}{GR}=\frac{QB}{CR}=\frac{JQ}{JC}$
Biến đổi góc ta cũng dễ chứng minh được $GQXR$ nội tiếp do đó ta có được $\Delta GQR\sim \Delta JQC(c-g-c)\Rightarrow \widehat{JXQ}=\widehat{JCQ}=\widehat{GRQ}=\widehat{GXQ}\Rightarrow$ $G, J, I, X$ thẳng hàng hay $IG$ là trục đẳng phương của $(XQC)$ và $(XBR)$
$\Rightarrow IG\perp ST$ hay $DK\perp ST$

Ý $a)$ phải là $O_1O_3//AC$ và $O_2O_4//BD$ chứ nhỉ
Chứng minh $a)$ Gọi $(I_2)$ tiếp xúc với $AC$ tại $G$, ta có $AG=\frac{AD-CD+AC}{2}$
                                $(I_4)$ tiếp xúc với $AC$ tại $G'$, ta có $AG'=\frac{AB-BC+AC}{2}$
Mặt khác $AD+BC=AB+CD$ (định lí Pithot) do đó ta có $AG=AG'$ hay $G\equiv G'$. Do đó $I_2I_4\perp AC\Rightarrow O_1O_3//AC$
Tương tự ta cũng có $O_2O_4//BD$
$b)$ Ta sẽ chứng minh một trường hợp tổng quát hơn: Cho tứ giác $ABCD$ ngoại tiếp $(I)$, đường thẳng bất kì $\perp AC$ cắt $IB, ID$ tại $M, N$. Đường thẳng bất kì $\perp BD$ cắt $IA, IC$ tại $P, Q$. Khi đó đường thẳng nối trung điểm của $MN$ và $PQ$ đi qua $I$
Chứng minh: Gọi $(I)$ tiếp xúc với $AB, BC, CA, AD$ tại $X, Y, Z, T$. Ta dễ thấy $AC, BD, XZ, YT$ đồng quy tại $S$
Một bổ đề quen thuộc: $XY, ZT, AC$ đồng quy tại $V$ và $XT, YZ, BD$ đồng quy tại $U$
Do đó theo Brocard ta có được $IV\perp BD$ hay $IV//PQ$
Mặt khác $(AC, SV)= B(AC, SV)= B(XY, SV) = -1$ do đó $IS$ đi qua trung điểm $PQ$, tương tự $IS$ đi qua trung điểm $MN$ hay ta có đpcm
Theo câu $a)$ thì ta đã có $I_2I_4\perp AC$ và $I_1I_3\perp BD$ nên theo bài toán trên thì ta có đpcm                   

$c)$ Chứng minh $A, O_1, I$ thẳng hàng bằng cách chứng minh $AI, AC$ đẳng giác trong $\widehat{I_2AI_4}$. Sau đó chứng minh tương tự như câu $b)$, thay vì yếu tố vuông góc thì đổi lại yếu tố song song                                 

Ta chứng minh $(AHD), (BHE), (CHF)$ đồng trục
Xét phép nghịch đảo cực $H$ phương tích $HA.HT$ ($T$ là chân đường cao từ $A$ tới $BC$) thì ta cần chứng minh $DD', EE', FF'$ đồng quy với $D', E', F'$ lần lượt là tâm đường tròn bàng tiếp góc $H$ của $\Delta HEF$, $\Delta HFD$, $\Delta HDE$
Có $\frac{sin\widehat{FDD'}}{sin\widehat{EDD'}}=\frac{D'F}{D'E}.\frac{sin\widehat{D'FD}}{sin\widehat{D'ED}}=\frac{sin\widehat{D'IF}}{sin\widehat{D'IE}}.\frac{sin(\widehat{DFE}+90^{\circ}-\frac{\widehat{HFE}}{2})}{sin(\widehat{DEF}+90^{\circ}-\frac{\widehat{HEF}}{2})}=\frac{sin(90^{\circ}-\frac{\widehat{HEF}}{2})}{sin(90^{\circ}-\frac{\widehat{HFE}}{2})}.\frac{sin(\widehat{DFE}+90^{\circ}-\frac{\widehat{HFE}}{2})}{sin(\widehat{DEF}+90^{\circ}-\frac{\widehat{HEF}}{2})}$
Tương tự cho các cặp còn lại, kết hợp với $H$ là tâm đường tròn nội tiếp $\Delta DEF$ nên ta có $DD', EE', FF'$ đồng quy
Vì vậy $(AHD), (BHE), (CHF)$ đồng trục. Do đó $AX, BY, CZ$ sẽ đồng quy tại một điểm nằm trên trục đẳng phương của 3 đường tròn này

Cho $ (O) $ và 1 điểm $A$  nằm ngoài $ (O) $

Tiếp tuyến $ AM,AN $

Cát tuyến $A,B,C$ .

$H$ là trung điểm $BC$

$OH \cap MN= \left \{ D \right \}, DC \cap AN=\left \{ F \right \}, AM\cap BD=\left \{ E \right \}$ . Chứng minh $MN,EF,BC$ đồng quy

$\cdot$ $D$ là giao hai tiếp tuyến tại $B, C$ của $(O)$
$\cdot$ Pascal $\begin{pmatrix} B &N &M\\ M& C&B \end{pmatrix}$ và $\begin{pmatrix} N &M&C \\ C &B &N \end{pmatrix}$

Cho tam giác ABC nội tiếp (O) có G nằm trên (O) sao cho AG là đường đối trung ứng với đỉnh A. A' đối xứng A qua O. M là trung điểm BC.AD là đường cao ứng với đỉnh A(D thuộc BC).A'M cắt (O) tại L.CMR:

a)L,D,G thẳng hàng

b)AA' cắt BC tại J. GJ cắt (O) tại T. CM TL//BC

a) Kẻ đường cao $BE, CF$ thì $AL, EF, BC$ đồng quy tại $X$. Do đó nếu gọi $AD$ cắt $(O)$ tại $S$ thì ta có $(LS, BC)$ = $A(LS, BC)$ = $A(XD, BC)=-1$ 
Do đó xét phép nghịch đảo cực $D$ phương tích $DB. DC$ sẽ có đpcm
b) Chứng minh $GMJA'$ nội tiếp. Để ý $BC$ phân giác góc $AMG$

Bài toán 20. Cho tam giác $ABC$ có $I$ là tâm nội tiếp. Đường tròn bàng tiếp góc $B,C$ lần lượt tiếp xúc với $AC,AB$ tại $X,Y$. Gọi $AD,AE$ là đường cao và đường phân giác của tam giác $ABC$. Chứng minh $DE$song song với tiếp tuyến tại $I$ của $(IDE)$.

Gọi $(J)$ là đường tròn bàng tiếp góc $A$, $R$ là hình chiếu của $J$ lên $BC$, $AI$ cắt $(O)$ tại $M$
Ta có $\Delta MBE\sim \Delta MAB(g-g)\Rightarrow \frac{MB}{ME}=\frac{BA}{BE}\Leftrightarrow \frac{MJ}{ME}=\frac{IA}{IE}\Leftrightarrow \frac{EJ}{EM}=\frac{EA}{EI}\Leftrightarrow \frac{EI}{EM}=\frac{EA}{EJ}=\frac{ED}{ER}$
$\Rightarrow ID//MR$. Gọi $ID$ cắt $MB, MC$ tại $P, Q$
Ta có $DP//MR$ nên $\frac{BM}{MP}=\frac{BR}{DR}$ $(1)$, $QD//MR$ nên $\frac{CM}{MQ}=\frac{CR}{RD}$ $(2)$
Từ $(1)$ và $(2)$ ta có được $\frac{MP}{MQ}=\frac{CR}{BR}=\frac{AY}{AX}$. Do đó $\Delta MPQ\sim \Delta AYX(c-g-c)$
Gọi $ID$ cắt $XY$ tại $N$ thì suy ra $\widehat{AYN}=\widehat{MPQ}=\widehat{NPB}$ hay $YNPB$ nội tiếp
$\Rightarrow \widehat{YNI}=180^{\circ}-\widehat{ABM}=\widehat{IED}$. Do đó có đpcm

Bài toán 2. Cho tam giác $\displaystyle ABC$ có trực tâm $\displaystyle H$ và $\displaystyle D,E,F$ lần lượt là hình chiếu của $\displaystyle A,B,C$ xuống $\displaystyle BC,CA,AB$. Gọi $\displaystyle L$ là điểm Lemoine của $\displaystyle ABC$ và $\displaystyle O$ là tâm ngoại tiếp của $\displaystyle ABC$. Chứng minh $\displaystyle OL$ đi qua trực tâm $\displaystyle DEF$.

Xin phép gửi một lời giải khác, mong mọi người góp ý
Bổ đề 1: Cho tam giác $ABC$ nội tiếp $(O)$, $(w_1), (w_2), (w_3)$ lần lượt là đường tròn $A- Apollonius, B- Apollonius, C- Apollonius$ của tam giác $ABC$. $L$ là điểm $Lemoine$. Khi đó $(w_1), (w_2), (w_3)$ đồng trục và có trục đẳng phương là đường thẳng $OL$
Bổ đề này quen thuộc nên mình xin phép không chứng minh
Bổ đề 2: Cho tam giác $ABC$ nội tiếp $(O)$ có các đường cao $AD, BE, CF$. $EF, FD, DE$ cắt $BC, CA, AB$ tại $X, Y, Z$. $T$ là trực tâm tam giác $DEF$. Khi đó các đường tròn $(XD), (YF), (ZE)$ đồng trục và có trục đẳng phương là đường thẳng $OT$
Chứng minh: Kẻ các đường cao $DD', EE', FF'$. Ta có $\overline{TD.TD'}=\overline{TE.TE'}=\overline{TF.TF'}$ hay $T$ có cùng phương tích với ba đường tròn $(XD), (YF), (ZE)$
Mặt khác ta có $(XD, BC)=-1$ nên đường tròn $(XD)$ trực giao với $(O)$, tương tự với các đường tròn $(YF), (ZE)$. Do đó $O$ có cùng phương tích với ba đường tròn $(XD), (YF), (ZE)$ là $R^2$
Vậy $OT$ là trục đẳng phương của $(XD), (YF), (ZE)$

Bổ đề 3: Cho tam giác $ABC$ có các đường cao $AD, BE, CF$. $M, N, P$ lần lượt là trung điểm $EF, FD, DE$. $MN, NP$ cắt $CB, BA$ tại $K, J$. Khi đó $KJ//AC$
Chứng minh: Ta có $\widehat{NJF}=\widehat{AFE}=\widehat{NFJ}\Rightarrow NJ=NF=ND\Rightarrow \widehat{FJD}=90^{\circ}$, tương tự $\widehat{FKD}=90^{\circ}$
Do đó $KJFD$ nội tiếp hay $\widehat{BJK}=\widehat{BDF}=\widehat{BAC}\Rightarrow KJ//AC$

Quay lại bài toán: Gọi $A_1, B_1, C_1$ lần lượt là chân đường tiếp tuyến từ $A, B, C$ tới $BC, CA, AB$ của $(O)$. Khi đó $A_1, B_1, C_1$ lần lượt là tâm của $(w_1), (w_2), (w_3)$ và $A_1, B_1, C_1$ thẳng hàng. Gọi $d$ là đường thẳng đi qua 3 điểm này
Gọi $X', Y', Z'$ lần lượt là trung điểm $XD, YF, ZE$. Khi đó $X', Y', Z'$ lần lượt là tâm của $(XD), (YF), (ZE)$ và $X', Y', Z'$ thẳng hàng. Gọi $d'$ là đường thẳng đi qua 3 điểm này
Theo bổ đề 1 ta có $OL$ vuông góc $d$, theo bổ đề 2 ta có $OT$ vuông góc $d'$. Do đó để chứng minh $O, L, T$ thẳng hàng thì ta cần chứng minh $d//d'$
Dễ thấy $X', J, N, P$ thẳng hàng và $Y', K, N, M$ thẳng hàng. Mặt khác $NP//EF//AA_1$ nên ta có $\frac{BX'}{BA_1}=\frac{BJ}{BA}$, tương tự $\frac{BY'}{BC_1}=\frac{BK}{BC}$
Mặt khác theo bổ đề 3 thì $JK//BC$ nên $\frac{BJ}{BA}=\frac{BK}{BC}$. Do đó $\frac{BX'}{BA_1}=\frac{BY'}{BC_1}$ nên $X'Y'//A_1C_1$ hay $d//d'$. Do đó ta có đpcm
P/s: sử dụng hình trong phần chứng minh bổ đề 3





 

Bài toán 19. Cho tam giác $ABC$ có tâm ngoại tiếp và trực tâm lần lượt là $O,H$. $M$ bất kỳ trên $(O)$, $N$ là điểm đối xứng của $M$ qua $BC$. $P$ là giao thứ hai của $AM$ và $(OMN)$. Chứng minh $HN$ đi qua trực tâm của $AOP$

Gọi $(OMN)$ giao $(O)$ tại điểm thứ hai là $F$, $AF$ cắt $HN$ tại $D$, $AH$ cắt $(O)$ tại $E$
Ta có $MNHE$ là hình thang cân nên $\widehat{DNM}=180^{\circ}-\widehat{AEM}=180^{\circ}-\widehat{DFM}\Rightarrow$ $DFMN$ nội tiếp
$\widehat{DAP}+\widehat{ADO}=\frac{1}{2}\widehat{FOM}+\widehat{OMF}=90^{\circ}\Rightarrow DO\perp AP$. Tương tự $PO\perp AD$ nên $D$ là trực tâm $\Delta AOP$

Một số tính chất mà em phát hiện được khi giải một bài toán, không biết đã có ở đâu hay chưa!

Bài toán 18. Cho $\Delta ABC$ ngoại tiếp $(I)$. $(I)$ tiếp xúc với $BC$ tại $D$. Qua $D$ kẻ đường thẳng vuông góc với $AI$ cắt $IB,IC$ tại $P,Q$.

a) Chứng minh rằng tứ giác $BQCP$ nội tiếp $(O)$. Khi đó hãy chứng minh $A,D,O$ thẳng hàng

b) $PQ$ cắt đường trung bình ứng với đỉnh $A$ của $\Delta ABC$ tại $R$. $S$ là trung điểm của $ID$. Chứng minh rằng $RS$ vuông góc với $AD$.

Screenshot (1539).png

a) Biến đổi góc dễ dàng có được $\widehat{PBC}=\widehat{PQC}$ nên $BQCP$ nội tiếp
Gọi $(I)$ tiếp xúc với $CA, AB$ tại $E, F$. $EF$ cắt $BC$ tại $G$, $BQ$ cắt $CP$ tại $H$. Ta sẽ chứng minh $I, H, G$ thẳng hàng
Điều này hiển nhiên vì $(GD, BC)=-1$ và $(HK, PC)=-1$ ($K$ là giao điểm của $ID$ và $PC$)
Do đó $I, G, H$ thẳng hàng. Mà $IG$ vuông góc $AD$ (tính chất quen thuộc), $IH$ vuông góc $DO$ (Brocard) nên $A, D, O$ thẳng hàng

b) Gọi $X$ là trực tâm $\Delta BIC$, $AI$ cắt $BC$ tại $T$, $L$ là tâm đường tròn bàng tiếp góc $A$
Đầu tiên dễ thấy $d$ là đường đối cực của $X$ (d là đường trung bình ứng với đỉnh $A$ của $\Delta ABC$), mà $R$ thuộc $d$ nên $X$ thuộc $d_R$
Mặt khác $T$ cũng thuộc $d_R$ nên $XT$ là đường đối cực của $R$
Gọi $I'$ đối xứng với $I$ qua $D$, $XT$ cắt đường thẳng qua $I'//BC$ tại $J$. Đầu tiên dễ thấy $I'$ và $S$ nghịch đảo nhau qua $(I)$ do đó $J$ là cực của $SR$ hay $SR$ vuông góc $IJ$
Do đó ta cần chứng minh $IJ//AD$
Thật vậy, ta có $\frac{IT}{TL}=\frac{IB.IC}{LB.LC}=\frac{I'B.I'C}{XC.XB}=\frac{I'D}{DX}=\frac{JT}{TX}\Rightarrow IJ//XL$
Mặt khác $XL//AD$ (biến đổi tỉ số đơn giản) nên $IJ//AD$. Đpcm
P/s: ở bài này $D, J, L$ cũng thẳng hàng luôn