Em có phần mềm hỗ trợ là IDM thì làm cách nào có thể down film trên 60s ạ ? Bác Magus giỏi mấy cái này vô giúp thằng em với.
Cảm ơn mọi người nhiều
evarist
Thống kê
- Nhóm: Thành viên
- Bài viết: 87
- Lượt xem: 3859
- Danh hiệu: Hạ sĩ
- Tuổi: Chưa nhập tuổi
- Ngày sinh: Chưa nhập ngày sinh
-
Giới tính
 Bí mật
Bí mật
-
Đến từ
Nam Định
-
Website URL
 http://mathnfriend.net
http://mathnfriend.net
1
Trung bình
Công cụ người dùng
Lần ghé thăm cuối
Ai biết down phim trên phim 60s ko
07-10-2008 - 14:28
Đàm đạo về bất đẳng thức hình học và bất đẳng thức đại số
12-05-2008 - 19:30
Bất đẳng thức hình học xưa nay luôn nổi tiếng với những vấn đề của riêng nó và đặc biệt là sự đẹp đẽ của chúng. Bạn cũng có thể nói : Thế à thế thì bất đẳng thức đại số cũng đẹp đấy chứ ? Tôi ko hề phủ nhận cũng ko hề thắc mắc gì cả trước hết tôi muốn các bạn thử trả lời câu hỏi : BDT Hình đẹp hơn hay BDT Đại đẹp hơn ? 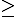
Hãy thử làm các bài toán sau :
Bài 1 : Cho tam giác ABC kí hiệu các yếu tố của tam giác như thường lệ. Chứng minh rằng$ xa^2+yb^2+zc^2\ge 4\sqrt{xy+yz+zx}S$ với $x,y,z\ge 0$
Bài 2 : Cho 3 số x,y,z dương. Chứng minh rằng :
$ \prod(\dfrac{x+y}{y+z}+\dfrac{y+z}{x+y})\le\dfrac{(x+y)^2(y+z)^2(z+x)^2}{8x^2y^2z^2}$
Mình bảo vệ quan điểm thứ 2 bất đẳng thức hình đẹp hơn có thể bài toán mình nêu ra chưa điển hình bởi mình ko làm bất đẳng thức đại đã khá lâu rồi tuy nhiên vẫn muốn các bạn nêu ra ý kiến của mình và cùng nhau thảo luận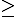
Hãy thử làm các bài toán sau :
Bài 1 : Cho tam giác ABC kí hiệu các yếu tố của tam giác như thường lệ. Chứng minh rằng$ xa^2+yb^2+zc^2\ge 4\sqrt{xy+yz+zx}S$ với $x,y,z\ge 0$
Bài 2 : Cho 3 số x,y,z dương. Chứng minh rằng :
$ \prod(\dfrac{x+y}{y+z}+\dfrac{y+z}{x+y})\le\dfrac{(x+y)^2(y+z)^2(z+x)^2}{8x^2y^2z^2}$
Mình bảo vệ quan điểm thứ 2 bất đẳng thức hình đẹp hơn có thể bài toán mình nêu ra chưa điển hình bởi mình ko làm bất đẳng thức đại đã khá lâu rồi tuy nhiên vẫn muốn các bạn nêu ra ý kiến của mình và cùng nhau thảo luận
Anh Kaka hãy trở lại
27-04-2008 - 20:08
Nghe đâu anh Kakalotta đã từ biệt VMF mà ko nói 1 lời. Được biết anh Kakalotta cũng rất nhiệt huyết với VMF và các mem của VMF cũng rất ủng hộ anh việc anh ra đi như thế thật đáng tiếc vì vậy em lập topic này mong anh em vào ủng hộ anh Kakalotta trở lại và chúng ta lại có những ngày vui vẻ vì đc xem post của anh 
Trước tiên vote cho anh Kaka 1 phiếu em mong anh trở lại
Trước tiên vote cho anh Kaka 1 phiếu em mong anh trở lại
GI 3
20-03-2008 - 16:26
Chứng minh rằng trong tam giác bất kì thì
$ a^2 + b^2 + c^2\ge 4\sqrt {4 -\sin\dfrac {A}{2}\sin\dfrac {B}{2}\sin\dfrac {C}{2}}S$
Và trong tam giác nhọn
$a^2 + b^2 + c^2\ge 4\sqrt {4 - cosAcosBcosC}S$ .
$ a^2 + b^2 + c^2\ge 4\sqrt {4 -\sin\dfrac {A}{2}\sin\dfrac {B}{2}\sin\dfrac {C}{2}}S$
Và trong tam giác nhọn
$a^2 + b^2 + c^2\ge 4\sqrt {4 - cosAcosBcosC}S$ .
Chứng minh rằng :$ ab + bc + ca\ge 4\sqrt {\dfrac {a...
20-03-2008 - 16:17
Chứng minh rằng :$ ab + bc + ca\ge 4\sqrt {\dfrac {a}{b} + \dfrac {b}{c} + \dfrac {c}{a}}S$
Nice I think
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Chủ đề: evarist


 Tìm kiếm
Tìm kiếm



