Đừng bảo cm thì nó ra thế nhá .
2201
Thống kê
- Nhóm: Thành viên
- Bài viết: 59
- Lượt xem: 2089
- Danh hiệu: Hạ sĩ
- Tuổi: Chưa nhập tuổi
- Ngày sinh: Chưa nhập ngày sinh
-
Giới tính
 Bí mật
Bí mật
-
Đến từ
Hà Nội
-
Website URL
 http://
http://
0
Trung bình
Công cụ người dùng
Lần ghé thăm cuối
Trong chủ đề: giúp em lớp 10 về nhị thức New-ton
17-10-2007 - 15:16
à hóa ra là ko phải hỏi cm thế làm ơn giải thích dùm vì sao có CT niu tơn kia 














Đừng bảo cm thì nó ra thế nhá .
Đừng bảo cm thì nó ra thế nhá .
Trong chủ đề: một bài nổi tiếng
17-10-2007 - 15:07
buy phông không phải người việt nam chữ các hay chữ vô số là do người việt nam dịch , còn bạn thắc mắc tại sao dùng các mà không dùng vô số thì bạn nên hỏi người dịch , còn mình thì chịu . Theo mình nó chẳng khác gì nhau .
Trong chủ đề: giúp em lớp 10 về nhị thức New-ton
08-10-2007 - 14:02
Đơn giản lắm em chứng minh bằng quy nạp là ra .
Trong chủ đề: Giúp mình bài này với
05-10-2007 - 10:41
đặt Sm=z^m+1/z^m
nên ta có : Sm=z^(m-1).(z+1/z)-z^(m-2)+[1/z^(m-1)].(z+1/z)-1/z^(m-2)
suy ra Sm=S(m-1)- S(m-2) = S(m-2)-S(m-3)+S(m-2)=-S(m-3)
suy ra Sm=S(m-6)
do 2002 chia 6 dư 4 nên S2002=S4=-S1
nên kq là S2002=-1
nên ta có : Sm=z^(m-1).(z+1/z)-z^(m-2)+[1/z^(m-1)].(z+1/z)-1/z^(m-2)
suy ra Sm=S(m-1)- S(m-2) = S(m-2)-S(m-3)+S(m-2)=-S(m-3)
suy ra Sm=S(m-6)
do 2002 chia 6 dư 4 nên S2002=S4=-S1
nên kq là S2002=-1
Trong chủ đề: một bài nổi tiếng
15-09-2007 - 20:04
Gọi A là sự kiện n bức thư đều gửi sai .
Ta tính xs của sự kiện B là ít nhất 1 bức thư gửi đúng, vậy P(A)=1-P(B)
Gọi Bi là xs bức thư thứ i gửi đúng =>P(Bi)=1/n
Vậy B=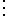 Bi
Bi
Dễ thấy
P(Bi)=1/n
P(BiBj)=P(Bi).P(Bj|Bi)=1/n.1/(n-1)
P(BiBjBk)=P(Bi).P(Bj|Bi).P(Bk\Bi.Bj)=1/n.1/(n-1).1/(n-2)
...
P(B1B2...Bn)=1/n!
Vậy theo CT cộng xs tổng quát: ( tạm kí hiệu C(k,n) là tổ hợp chập k của n phần tử nhé )
P(B)=C(1,n).1/n-C(2,n).(n-2)!/n!+C(3,n).(n-3)!/n!-...+(-1)^(n+1).C(n,n).1/n!
=1-1/2!+1/3!-...+(-1)^(n+1).1/n!
Vậy P(A)=1-P(B).
Nếu n khá lớn thì P(A)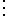 1/e.
1/e.
Ta tính xs của sự kiện B là ít nhất 1 bức thư gửi đúng, vậy P(A)=1-P(B)
Gọi Bi là xs bức thư thứ i gửi đúng =>P(Bi)=1/n
Vậy B=
Dễ thấy
P(Bi)=1/n
P(BiBj)=P(Bi).P(Bj|Bi)=1/n.1/(n-1)
P(BiBjBk)=P(Bi).P(Bj|Bi).P(Bk\Bi.Bj)=1/n.1/(n-1).1/(n-2)
...
P(B1B2...Bn)=1/n!
Vậy theo CT cộng xs tổng quát: ( tạm kí hiệu C(k,n) là tổ hợp chập k của n phần tử nhé )
P(B)=C(1,n).1/n-C(2,n).(n-2)!/n!+C(3,n).(n-3)!/n!-...+(-1)^(n+1).C(n,n).1/n!
=1-1/2!+1/3!-...+(-1)^(n+1).1/n!
Vậy P(A)=1-P(B).
Nếu n khá lớn thì P(A)
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Bài viết: 2201


 Tìm kiếm
Tìm kiếm


