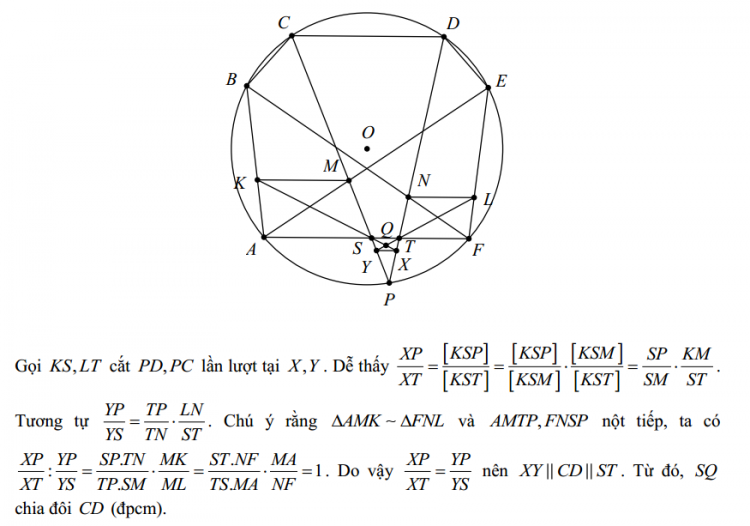
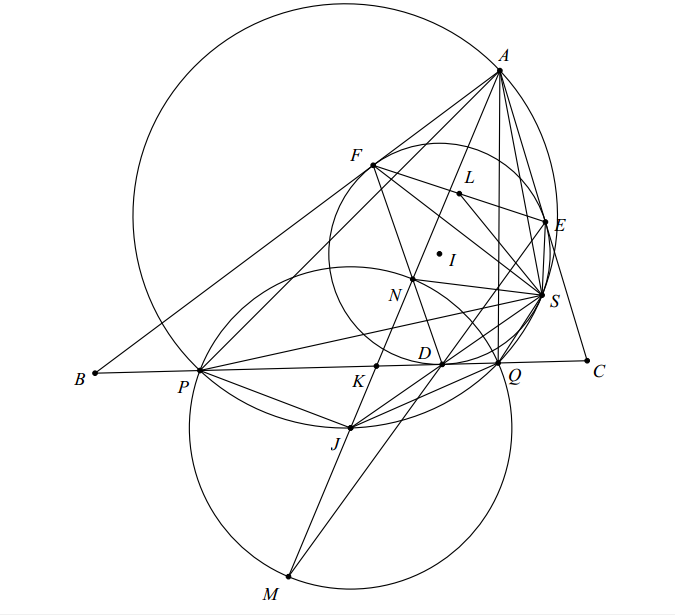
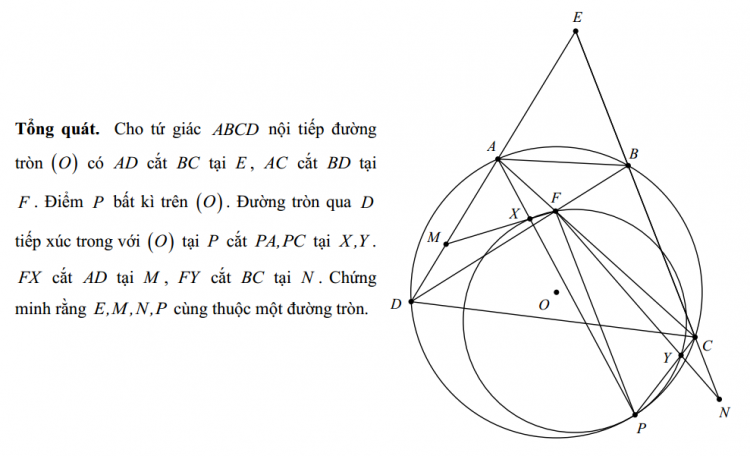
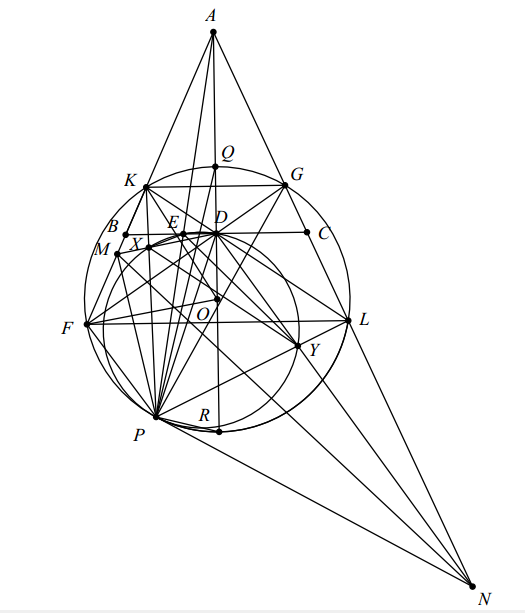
Chứng minh của em bị lỗi nặng ạ
cách giải của anh đã khắc phục được
Nhân tiện, anh có thể đăng bài toán gốc cho mọi người tham khảo được không ạ ?
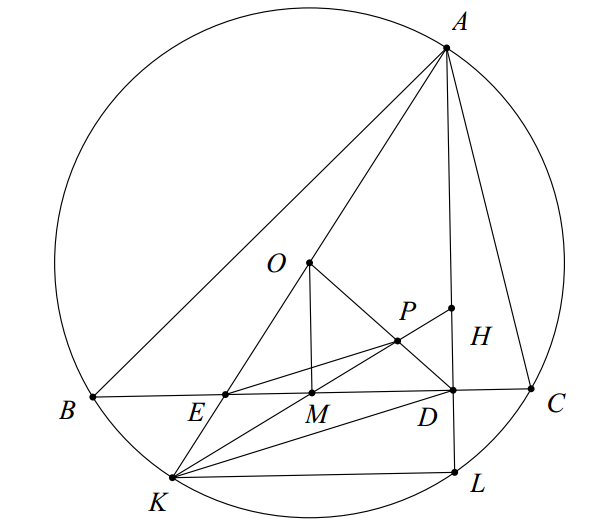
Bài toán gốc là trường hợp riêng của bài toán 2 khi $E$ trùng $F$. Lúc đó, kết luận trở thành trung tuyến đỉnh $A$ của tam giác $ABC$ đi qua trực tâm tam giác $DMN$.
- Zeref yêu thích



 Tìm kiếm
Tìm kiếm Bí mật
Bí mật