Tên : Nguyễn Thái phúc
Lớp: 12A2 toán, trường THPT chuyên KTHN, thành phố Hà Nôi
Địa chỉ nhận sách: có thể đưa cho em Đăng Quả nhận hộ, hình như em ấy có đi offline
- E. Galois, perfectstrong và Zaraki thích
 Nam
Nam
 Gửi bởi nguyen thai phuc
trong 18-07-2012 - 23:12
Gửi bởi nguyen thai phuc
trong 18-07-2012 - 23:12
 Gửi bởi nguyen thai phuc
trong 18-07-2012 - 18:11
Gửi bởi nguyen thai phuc
trong 18-07-2012 - 18:11
 Gửi bởi nguyen thai phuc
trong 16-04-2012 - 23:12
Gửi bởi nguyen thai phuc
trong 16-04-2012 - 23:12
 Gửi bởi nguyen thai phuc
trong 29-02-2012 - 21:27
Gửi bởi nguyen thai phuc
trong 29-02-2012 - 21:27
 Gửi bởi nguyen thai phuc
trong 23-02-2012 - 23:02
Gửi bởi nguyen thai phuc
trong 23-02-2012 - 23:02
 Gửi bởi nguyen thai phuc
trong 19-01-2012 - 21:58
Gửi bởi nguyen thai phuc
trong 19-01-2012 - 21:58
 wetzen.pdf 418.3K
460 Số lần tải
wetzen.pdf 418.3K
460 Số lần tải
 Gửi bởi nguyen thai phuc
trong 16-12-2011 - 23:24
Gửi bởi nguyen thai phuc
trong 16-12-2011 - 23:24
 Gửi bởi nguyen thai phuc
trong 16-12-2011 - 22:13
Gửi bởi nguyen thai phuc
trong 16-12-2011 - 22:13
 Gửi bởi nguyen thai phuc
trong 26-11-2011 - 23:32
Gửi bởi nguyen thai phuc
trong 26-11-2011 - 23:32
Bài 64: Cho $a,b,c >0$ Chứng minh rằng:$$\dfrac{1}{a^{2}+ab+b^{2}}+\dfrac{1}{b^{2}+bc+c^{2}}+\dfrac{1}{c^{2}+ca+a^{2}}\ge\dfrac{9abc(a+b+c)}{(ab+bc+ca)^{3}}$$
Nguồn:Ôn luyện toán
 Gửi bởi nguyen thai phuc
trong 26-11-2011 - 15:10
Gửi bởi nguyen thai phuc
trong 26-11-2011 - 15:10
${{P}_{n}}\left( x \right)=\sum\limits_{k=0}^{n}{\dfrac{{{x}^{k}}}{k!}}\Rightarrow P_{n}^{'}\left( x \right)={{P}_{n-1}}\left( x \right)$Bài 9:CMR với mọi số nguyên dương $n$ thì đa thức sau không thể có nhiều hơn một nghiệm thực
\[P(x) = 1 + x + \dfrac{{{x^2}}}{{x!}} + ... + \dfrac{{{x^n}}}{{n!}}\]
@@Mọi người cùng gửi những bài toán hay về đa thứ mà mọi người biết lên để tham khảo nhé
 Gửi bởi nguyen thai phuc
trong 28-05-2011 - 17:22
Gửi bởi nguyen thai phuc
trong 28-05-2011 - 17:22
Lâu lắm mới vào vmf, làm tí cho xôm tụDạo này nghỉ hè rỗi rãi sáng tác 1 bài tặng các bạn nhân dịp cuối năm học
Cho $a,b,c>0 $ thỏa mãn $ a^2+b^2+c^2=1 $.Chứng minh:
$ \dfrac{c+ab}{\sqrt{1-a^2}}+\dfrac{a+bc}{\sqrt{1-b^2}}+\dfrac{b+ca}{\sqrt{1-c^2}} \le \sqrt{6+3a+3b+3c} $
 Gửi bởi nguyen thai phuc
trong 02-02-2011 - 16:10
Gửi bởi nguyen thai phuc
trong 02-02-2011 - 16:10
 Gửi bởi nguyen thai phuc
trong 13-08-2010 - 19:28
Gửi bởi nguyen thai phuc
trong 13-08-2010 - 19:28
Hê hê. Bài này em làm được nàyĐề này chắc bài cuối khó nhất! Chẳng hiểu bọn lớp 9 làm như nào
Mò mẩm ra cái đẳng thức này: $x^{15}-1=(x-1)(x^2+x+1)(x^4+x^3+x^2+x+1)(x^8 - x^7 + x^5 - x^4 + x^3 - x + 1 )$ Suy ra pt vô nghiệm
Cái này trong phòng thi chắc ko ra được
 Gửi bởi nguyen thai phuc
trong 24-02-2010 - 16:40
Gửi bởi nguyen thai phuc
trong 24-02-2010 - 16:40
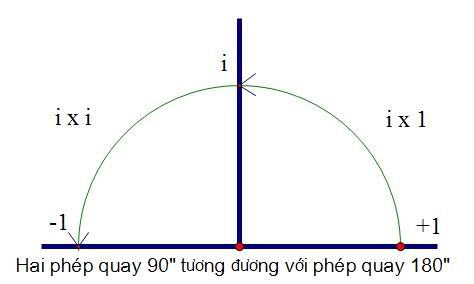
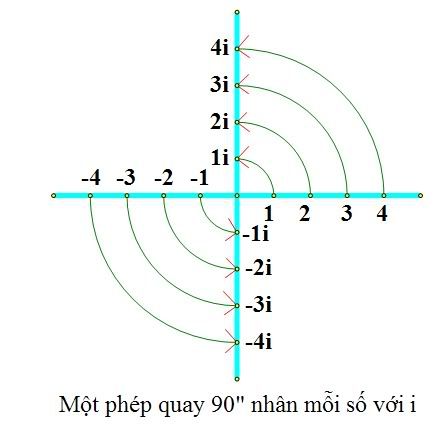
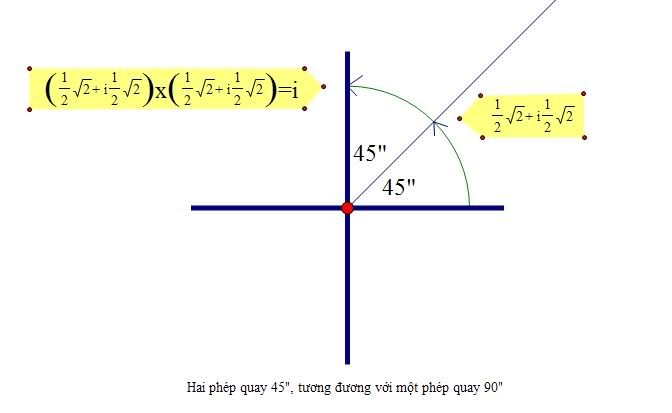
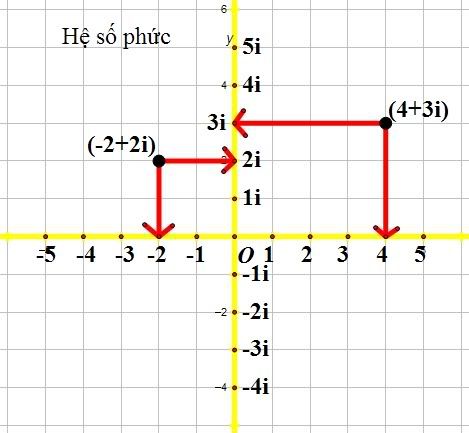
 Gửi bởi nguyen thai phuc
trong 24-02-2010 - 13:43
Gửi bởi nguyen thai phuc
trong 24-02-2010 - 13:43
Làm sao mà c/m được. Em thấy câu b vô lí đùng đùng.Đây là lời giải chi tiết của em.Câu 2 thì chứng minh thêm ab+bc+Ca>0 là suy ra a,b,c>0 nên đưa lại về câu a

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học

 Tìm kiếm
Tìm kiếm