Mình sẽ giải chi tiết bài này cho bạn hiểu hơn
Dễ dàng bạn tìm được độ dài cạnh $AB = a;AC = a\sqrt 3 $
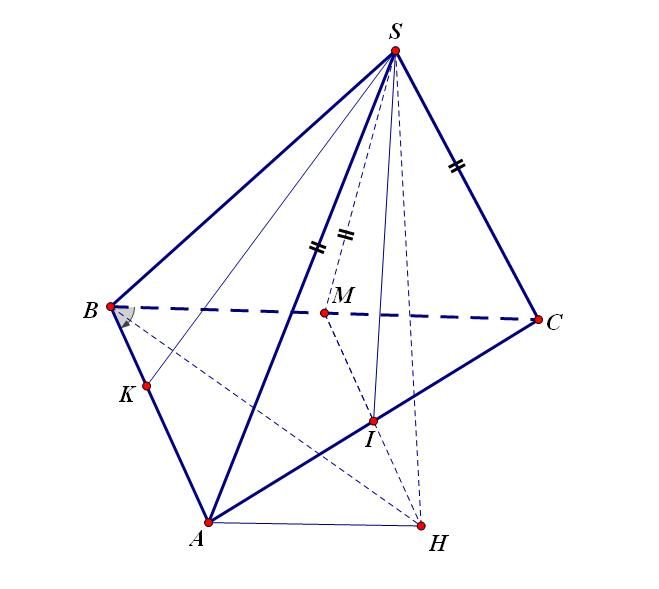
Gọi $I$ là trung điểm của AC
Gọi $H$ là chân đường vuông góc hạ từ S lên$MI$
Ta có
$\left\{ \begin{array}{l}
MH \bot AC{\rm{ do }}(MI{\rm{ song song }}AB) \\
SI \bot AC \\
\end{array} \right. \Rightarrow AC \bot \left( {SHI} \right)$
$ \Rightarrow SH \bot AC\left( 1 \right)$
Lại có $SH \bot MI\left( 2 \right)$
Từ (1), (2):
$\left\{ \begin{array}{l}
SH \bot AC \\
SH \bot MI \\
MI,AC \subset \left( {ABC} \right) \\
\end{array} \right. \Rightarrow SH \bot \left( {ABC} \right)$
$ \Rightarrow d\left( {S,\left( {ABC} \right)} \right) = SH$
* Tính $SH$
$\begin{array}{l}
S{M^2} = M{I^2} + S{I^2} - 2MI.SI.\cos \left( {SIM} \right) \\
\Leftrightarrow \cos \left( {SIM} \right) = \frac{{M{I^2} + S{I^2} - S{M^2}}}{{2MI.SI}} = \frac{{\frac{{{a^2}}}{4} + \frac{{17{a^2}}}{4} - 5{a^2}}}{{2.\frac{a}{2}.\frac{{a\sqrt {17} }}{2}}} = \frac{{ - \frac{{{a^2}}}{2}}}{{\frac{{{a^2}\sqrt {17} }}{2}}} = - \frac{{\sqrt {17} }}{{17}} \\
\end{array}$
$\cos \left( {SIM} \right) = - \frac{{\sqrt {17} }}{{17}}$ nghĩa là góc (SIM) lớn hơn ${90^0}$
Do đó, chân đường cao $H$ nằm ngoài đoạn $MI$ và về phía $I$
$ \Rightarrow \cos \left( {SIH} \right) = \frac{{HI}}{{SI}} = \frac{{\sqrt {17} }}{{17}} \Leftrightarrow HI = \frac{{\sqrt {17} }}{{17}}.\frac{{a\sqrt {17} }}{2} = \frac{a}{2}$
$\begin{array}{l}
\Rightarrow MH = a \\
\Rightarrow MH = AB = a \\
\end{array}$
Xét tam giác $SHI$ vuông tại $H$:
$S{H^2} = S{I^2} - I{H^2} = \frac{{17{a^2}}}{4} - \frac{{{a^2}}}{4} = 4{a^2} \Leftrightarrow SH = 2a$
$ \Rightarrow d\left( {S,\left( {ABC} \right)} \right) = SH = 2a$
Dễ thấy $ABMH$ là hình chữ nhật
$ \Rightarrow B{H^2} = A{B^2} + A{H^2} = 2{a^2} \Rightarrow BH = a\sqrt 2 $
Xét tam giác $SHB$ vuông tại $H$:
$S{B^2} = S{H^2} + B{H^2} = 4{a^2} + 2{a^2} = 6{a^2} \Rightarrow SB = a\sqrt 6 $
Xét tam giác $SAB$:
$\cos \left( {SBA} \right) = \frac{{A{B^2} + S{B^2} - S{A^2}}}{{2AB.SB}} = \frac{{{a^2} + 6{a^2} - 5{a^2}}}{{2{a^2}\sqrt 6 }} = \frac{{\sqrt 6 }}{6}$
Xét tam giác $SBK$ vuông tại $K$:
$\cos \left( {SBK} \right) = \frac{{BK}}{{SB}} = \frac{{\sqrt 6 }}{6} \Leftrightarrow BK = a$
$S{K^2} = S{B^2} - B{K^2} = 6{a^2} - {a^2} = 5{a^2} \Leftrightarrow SK = a\sqrt 5 $
$ \Rightarrow d\left( {S,AB} \right) = SK = a\sqrt 5 $
Quy trình tính toán là như vậy, có thể mình tính sai số nên bạn có thể tính lại kỹ hơn
$------------------------------------------------------------------------------$
Chắc có lẽ cách xác định khoảng cách từ điểm tới mặt phẳng là khó với một số bạn:
Mình sẽ trình bày phương pháp tìm hình chiếu của điểm lên mặt
* Dể tìm hình chiếu $H$ của điểm $M$ lên mặt phẳng $P$ cho trước:
Ta tìm một mặt phẳng $(Q)$ đi qua điểm $M$ vuông góc với mặt phẳng $(P)$ cắt $(P)$ theo giao tuyến $d$.
Từ đó ta dựng $MH \bot d$. Khi đó $H$ là hình chiếu của $M$ lên $(P)$ hay $d(M,(P))=MH$
Áp dụng cho bài toán trên: Mình đã xác định được mặt phẳng $(SMI)$ đi qua điểm $S$ vuông góc với $(ABC)$ và có giao tuyến là $MI$ nên ta dựng $SH$ vuông góc với $MI$ thì $SH$ chính là $d(S,(ABC))$
- 200dong yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam
 Gửi bởi
Gửi bởi