${d_1}\left( {x,y} \right) = \int\limits_0^1 {\left| {y\left( t \right) - x\left( t \right)} \right|dt} $
Chứng minh ${d_1}$ là metric trên $X = {C_{\left[ {0;1} \right]}}$
- funcalys yêu thích
Hội An trung thu những ngày mưa buồn
 Nam
Nam
 Gửi bởi vantho302
trong 30-09-2012 - 21:11
Gửi bởi vantho302
trong 30-09-2012 - 21:11
 Gửi bởi vantho302
trong 30-09-2012 - 12:36
Gửi bởi vantho302
trong 30-09-2012 - 12:36
 Gửi bởi vantho302
trong 29-09-2012 - 08:44
Gửi bởi vantho302
trong 29-09-2012 - 08:44
 Gửi bởi vantho302
trong 27-09-2012 - 08:20
Gửi bởi vantho302
trong 27-09-2012 - 08:20
 Gửi bởi vantho302
trong 26-09-2012 - 19:47
Gửi bởi vantho302
trong 26-09-2012 - 19:47
 Gửi bởi vantho302
trong 25-09-2012 - 07:03
Gửi bởi vantho302
trong 25-09-2012 - 07:03
 Gửi bởi vantho302
trong 24-09-2012 - 11:25
Gửi bởi vantho302
trong 24-09-2012 - 11:25
 Gửi bởi vantho302
trong 17-09-2012 - 12:58
Gửi bởi vantho302
trong 17-09-2012 - 12:58
 Gửi bởi vantho302
trong 31-08-2012 - 21:42
Gửi bởi vantho302
trong 31-08-2012 - 21:42
 Gửi bởi vantho302
trong 02-08-2012 - 01:21
Gửi bởi vantho302
trong 02-08-2012 - 01:21
 Gửi bởi vantho302
trong 22-07-2012 - 16:55
Gửi bởi vantho302
trong 22-07-2012 - 16:55
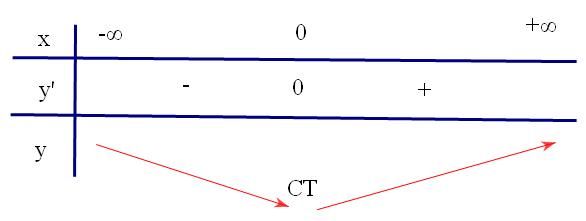
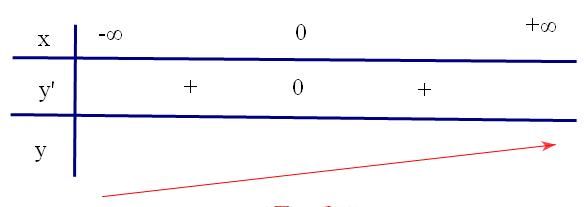
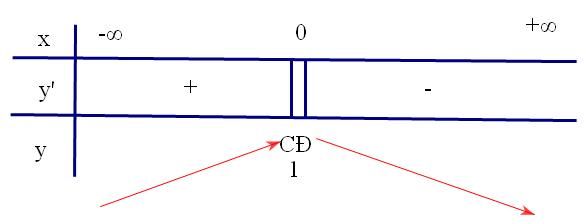
 Gửi bởi vantho302
trong 27-06-2012 - 08:35
Gửi bởi vantho302
trong 27-06-2012 - 08:35
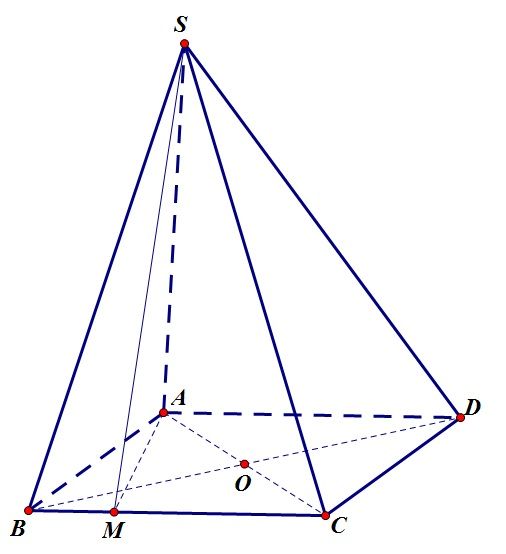
 Gửi bởi vantho302
trong 27-06-2012 - 06:37
Gửi bởi vantho302
trong 27-06-2012 - 06:37

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học

 Tìm kiếm
Tìm kiếm