vantho302

Bài toán trên sẽ có hai trường hợp như sau:

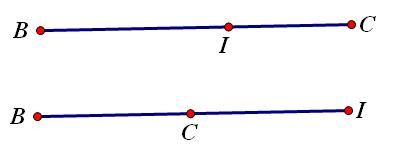
* Trường hợp 1: Điểm I nằm giữa BC. Khi đó ta có \[\overrightarrow {IB} = - 2\overrightarrow {IC} \]
Ta có: \[\overrightarrow {BC} = \left( { - 2,1, - 4} \right)\]
Phương trình tham số của đường thẳng (BC):
\[\left\{ \begin{array}{l}
x = 1 - 2t \\
y = 1 + t \\
z = 2 - 4t \\
\end{array} \right.;t \in R\]
Vì điểm I thuộc (BC) nên tọa độ điểm I thỏa: \[I\left( {1 - 2t;1 + t;2 - 4t} \right)\]
\[ \Rightarrow \overrightarrow {IB} = \left( {2t, - t,4t} \right);\overrightarrow {IC} = \left( { - 2 + 2t;1 - t; - 4 + 4t} \right)\]
\[\overrightarrow {IB} = - 2\overrightarrow {IC} \]
\[ \Rightarrow \left\{ \begin{array}{l}
2t = 4 - 4t \\
- t = - 2 + 2t \\
4t = 8 - 8t \\
\end{array} \right. \Leftrightarrow t = \frac{2}{3}\]
\[ \Rightarrow I\left( { - \frac{1}{3};\frac{5}{3}; - \frac{2}{3}} \right) \Rightarrow \overrightarrow {AI} = \left( { - \frac{4}{3};\frac{2}{3};\frac{1}{3}} \right) = \frac{1}{3}\left( { - 4;2;1} \right)\]
Lại có mặt phẳng (P): \[x - 2y + 2z + 1 = 0\] vuông góc với mặt phẳng \[\left( \alpha \right)\] nên \[\overrightarrow {{n_P}} = \overrightarrow {{u_\alpha }} = \left( {1; - 2;2} \right)\]
Do đó véctơ pháp tuyến của mặt phẳng \[\left( \alpha \right)\] là \[\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {AI} ,\overrightarrow {{u_\alpha }} } \right] = \left( {6;9;6} \right) = 3\left( {2;3;2} \right)\]
Phương trình mặt phẳng \[\left( \alpha \right)\] có dạng:
\[2\left( {x - 1} \right) + 3\left( {y - 1} \right) + 2\left( {z + 1} \right) = 0 \Leftrightarrow 2x + 3y + 2z - 3 = 0\]
* Trường hợp 2: Điểm C nằm giữa B và I nghĩa là C là trung điểm của BI
\[ \Rightarrow \left\{ \begin{array}{l}
{x_I} = 2{x_C} - {x_B} \\
{y_I} = 2{y_C} - {y_B} \\
{z_I} = 2{z_C} - {z_B} \\
\end{array} \right. \Leftrightarrow I\left( { - 3;3; - 6} \right)\]
\[ \Rightarrow \overrightarrow {IA} = \left( {4; - 2;5} \right)\]
\[ \Rightarrow \overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {IA} ,\overrightarrow {{n_P}} } \right] = \left( {6; - 3; - 6} \right) = 3\left( {2; - 1; - 2} \right)\]
Phương trình mặt phẳng \[\left( \alpha \right)\] có dạng:
\[2\left( {x - 1} \right) - 1\left( {y - 1} \right) - 2\left( {z + 1} \right) = 0 \Leftrightarrow 2x - y - 2z - 3 = 0\]
Vậy ta có hai phương trình mặt phẳng \[\left( \alpha \right)\] thỏa mãn điều kiện trên:
\[2x - y - 2z - 3 = 0\] và \[2x + 3y + 2z - 3 = 0\]

* Xác định mặt phẳng (P), trong mặt phẳng (SAC), $SO \cap AC' = G$
Trong mặt phẳng (SBD), Từ G vẽ đường thẳng song song với BD cắt SB, SD lần lượt tại B’ và D’. Khi đó mặt phẳng (P) chính là mặt phẳng (AB’C’D’)
Ta có AC và BD là hai đường chéo của hình thoi ABCD nên $AC \bot BD$
Góc $\widehat{BAD} = {60^0} \Rightarrow \widehat{BAO} = {30^0}$
Xét tam giác vuông BOA vuông tại O
$\cos \left( {BAO} \right) = \cos {30^0} = \frac{{AO}}{{AB}} = \frac{{\sqrt 3 }}{2} \Leftrightarrow AO = \frac{{a\sqrt 3 }}{2}$
G chính là trọng tâm của tam giác SAC nên $\frac{{SG}}{{SO}} = \frac{2}{3}$
Xét tam giác SBD, ta có B’D’ song song với BD, có $SB = SD$
$\frac{{SB'}}{{SB}} = \frac{{SD'}}{{SD}} = \frac{{SG}}{{SO}} = \frac{2}{3}$
$AC = 2AO = a\sqrt 3 $
$\sin \left( {BAO} \right) = \sin {30^0} = \frac{{BO}}{{AB}} = \frac{1}{2} \Leftrightarrow BO = \frac{a}{2} \Leftrightarrow BD = a$
${S_{ABCD}} = \frac{1}{2}AC.BD = \frac{{{a^2}\sqrt 3 }}{2}$
$ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}$
$\begin{array}{l}
\frac{{{V_{S.AB'C'D'}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{SAB'C'}}}}{{{V_{SABC}}}} + \frac{{{V_{SAC'D'}}}}{{{V_{SACD}}}} \\
= \frac{{SA}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} + \frac{{SA}}{{SA}}.\frac{{SC'}}{{SC}}.\frac{{SD'}}{{SD}} = 2\left( {\frac{{SA}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}} \right) = 2.\frac{2}{3}.\frac{1}{2} = \frac{2}{3} \\
\Leftrightarrow {V_{S.AB'C'D'}} = \frac{2}{3}{V_{S.ABCD}} = \frac{2}{3}.\frac{{{a^3}\sqrt 3 }}{6} = \frac{{{a^3}\sqrt 3 }}{9} \\
\end{array}$

Gọi A' là điểm đối xứng với A qua đường phân giác trong CD
Phương trình đường thẳng AA' vuông góc với CD và A' thuộc BC có dạng
\[1\left( {x - 1} \right) - \left( {y - 2} \right) = 0 \Leftrightarrow x - y + 1 = 0\]
Gọi I là giao điểm của AA'. Khi đó I là giao điểm của AA' và CD
\[ \Rightarrow \left\{ \begin{array}{l}
x - y + 1 = 0 \\
x + y - 1 = 0 \\
\end{array} \right. \Rightarrow I\left( { 0;1} \right)\]
I là trung điểm của AA'\[ \Rightarrow A'\left( { - 1, 0} \right)\]
* M là trung điểm AC\[ \Rightarrow M\left( {\frac{{{x_C} + 1}}{2};\frac{{{y_C} + 2}}{2}} \right)\]
Điểm M thuộc BM: \[2x + y + 1 = 0\]
\[ \Rightarrow {x_C} + 1 + \frac{{{y_C} + 2}}{2} + 1 = 0 \Leftrightarrow 2{x_C} + {y_C} + 6 = 0\]
Điểm C thuộc vào đường phân giác CD: \[x + y + 1 = 0 \Rightarrow {x_C} + {y_C} + 1 = 0\]
kết hợp hai phương trình :
\[\left\{ \begin{array}{l}
2{x_C} + {y_C} + 6 = 0 \\
{x_C} + {y_C} - 1 = 0 \\
\end{array} \right. \Leftrightarrow C\left( { - 7,8} \right)\]
Ta có \[\overrightarrow {CA'} = \left( {6, - 8} \right) = 2\left( {3, - 4} \right)\] là vecto chỉ phương của phương trình đường BC
\[ \Rightarrow \left( {BC} \right):4\left( {x + 1} \right) + 3\left( {y + 0} \right) = 0 \Leftrightarrow 4x + 3y + 4 = 0\]
Chúc bạn thi tốt

Chuyển phương trình (d) về dạng tham số:
\[\left( d \right):\left\{ \begin{array}{l}
x = t \\
y = - 2 - t \\
z = 1 + t \\
\end{array} \right.,t \in \]
Vì M thuộc (d) nên M có tọa độ \[M\left( {t; - 2 - t;1 + t} \right)\]
* Xét mặt phẳng (ABM)
\[\begin{array}{l}
\overrightarrow {AB} = \left( { - 1;1;1} \right);\overrightarrow {AM} = \left( {t - 1; - 2 - t;1 + t} \right) \\
\Rightarrow \overrightarrow {{n_{\left( {ABM} \right)}}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( {2t + 3;2t;3} \right) \\
\end{array}\]
* Xét mặt phẳng (ABC)
\[\begin{array}{l}
\overrightarrow {AB} = \left( { - 1,1,1} \right);\overrightarrow {BC} = \left( {0, - 1;1} \right) \\
\Rightarrow \overrightarrow {{n_{\left( {ABC} \right)}}} = \left( {2,1,1} \right) \\
\end{array}\]
* góc giữa (ABM) và (ABC) là \[{30^0}\]
\[\begin{array}{l}
\cos \left( {30} \right) = \frac{{\left| {\overrightarrow {{n_{ABM}}} .\overrightarrow {{n_{ABC}}} } \right|}}{{\left| {\overrightarrow {{n_{ABM}}} } \right|.\left| {\overrightarrow {{n_{ABC}}} } \right|}} = \frac{{\left| {6t + 9} \right|}}{{\sqrt 6 .\sqrt {{{\left( {2t + 3} \right)}^2} + 4{t^2} + 9} }} = \frac{{\sqrt 3 }}{2} \\
\Leftrightarrow \left| {6t + 9} \right| = \frac{{\sqrt {18} }}{2}\sqrt {4{t^2} + 16t + 18} \Leftrightarrow {\left( {6t + 9} \right)^2} = \frac{9}{2}\left( {4{t^2} + 16t + 18} \right) \\
\Leftrightarrow 18{t^2} + 36t = 0 \Leftrightarrow \left[ \begin{array}{l}
t = 0 \\
t = - 2 \\
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
{M_1} = \left( {0, - 2,1} \right) \\
{M_2} = \left( { - 2,0, - 1} \right) \\
\end{array} \right. \\
\end{array}\]

Mặt phẳng (P), cách đều C, D sẽ xảy ra 2 trường hợp:
* Trường hợp 1: C, D nằm cùng phía với (P)

Suy ra \[\overrightarrow {CD} = \left( {3,3,2} \right)\] có giá song song với (P)
(P) đi qua A, B có \[\overrightarrow {AB} = \left( {2,1, - 1} \right)\]
\[ \Rightarrow \overrightarrow {{n_\pi }} = \left[ {\overrightarrow {CD} ,\overrightarrow {AB} } \right] = \left( {5, - 7,3} \right)\]
Phương trình mặt phawrhg (P) có dạng: \[5\left( {x - 1} \right) - 7\left( {y - 1} \right) + 3\left( {z - 1} \right) = 0 \Leftrightarrow 5x - 7y + 3z - 1 = 0\]
* Trường hợp 2: C, D nằm khác phía đối với (P)

Khi đó trung điểm của CD luôn nằm trên mặt phẳng (P), Gọi M là trung điểm CD suy ra tọa độ \[M\left( {\frac{{11}}{2},\frac{5}{2},1} \right)\]

\[\begin{array}{l}
\overrightarrow {AB} = \left( {2,1, - 1} \right);\overrightarrow {AM} = \left( {\frac{9}{2},\frac{3}{2},0} \right) \\
\Rightarrow \overrightarrow {{n_P}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( {\frac{3}{2}, - \frac{9}{2}, - \frac{3}{2}} \right) = \frac{3}{2}\left( {1, - 3, - 1} \right) \\
\end{array}\]

Phương trình mặt phẳng (P) có dạng: \[1\left( {x - 1} \right) - 3\left( {y - 1} \right) - 1\left( {z - 1} \right) = 0 \Leftrightarrow x - 3y - z + 3 = 0\]

Ta sẽ chứng minh được
$\begin{array}{l}
AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\\
AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC\\
\Rightarrow SC \bot \left( {AHK} \right)
\end{array}$
* Tìm giao tuyến của (SAC) và (AHK)
Trong mặt phẳng (SBD), $SO \cap HK = M$
\[ \Rightarrow \left\{ \begin{array}{l}
\left( {AHK} \right) \cap \left( {SAC} \right) = \left\{ M \right\}\\
\left( {AHK} \right) \cap \left( {SAC} \right) = \left\{ A \right\}
\end{array} \right.\]
Hay \[\left( {AHK} \right) \cap \left( {SAC} \right) = AM\]
Kéo dài AM cắt SC tại N. Từ đó AN là đường giao tuyến của (SAC) và (AHK)
Ta có
$\begin{array}{l}
SC \bot \left( {AHK} \right)\\
\Rightarrow SN \bot \left( {AHK} \right)
\end{array}$
Do đó, SN là đường cao của hình chóp ${V_{S.AHK}} = \frac{1}{3}SN.{S_{\Delta AHK}}$ (mình mượn hình chóp này để tìm ${S_{\Delta AHK}}$ )
* Tính SN
Xét tam giác SAC vuông tại A có AN là đường cao
$\frac{1}{{A{N^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{O^2}}} \Leftrightarrow A{N^2} = {a^2}$
Xét tam giác SAN vuông tại N, $S{N^2} = S{A^2} - A{N^2} = 2{a^2} - {a^2} = {a^2}$
$ \Rightarrow SN = a$
* Tính ${V_{S.AHK}}$
Ta có ${V_{S.ABD}} = \frac{1}{3}SA.{S_{\Delta ABD}} = \frac{1}{3}a\sqrt 2 .\frac{{{a^2}}}{2} = \frac{{\sqrt 2 {a^3}}}{6}$
Và $\Delta SAB = \Delta SAD \Rightarrow SB = SD$
H, K chia SB và SD những đoạn thẳng tỉ lệ nhau
$\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}$
* Xét $\Delta SAB$ vuông tại A, có đường cao AH
$S{B^2} = S{A^2} + A{B^2} = 2{a^2} + {a^2} = 3{a^2} \Leftrightarrow SB = a\sqrt 3 $
$\begin{array}{l}
S{A^2} = SH.SB \Leftrightarrow SH = \frac{{S{A^2}}}{{SB}} = \frac{{2{a^2}}}{{a\sqrt 3 }} = \frac{{2a\sqrt 3 }}{3}\\
\Rightarrow \frac{{SH}}{{SB}} = \frac{2}{3}
\end{array}$
$ \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} = \frac{2}{3}$
Phương pháp tỉ lệ khối chóp:
$\frac{{{V_{S.AHK}}}}{{{V_{S.ABD}}}} = \frac{{SA}}{{SA}}.\frac{{SH}}{{SB}}.\frac{{SK}}{{SD}} = \frac{4}{9}$
$ \Leftrightarrow {V_{S.AHK}} = \frac{4}{9}{V_{S.ABD}} = \frac{4}{9}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{2{a^3}\sqrt 2 }}{{27}}$
* Tính ${S_{\Delta AHK}}$
${V_{S.AHK}} = \frac{1}{3}SN.{S_{\Delta AHK}} = \frac{1}{3}a.{S_{\Delta AHK}} = \frac{{2{a^3}\sqrt 2 }}{{27}} \Leftrightarrow {S_{\Delta AHK}} = \frac{{2{a^2}\sqrt 2 }}{9}$
* Xác định đường cao của hình chóp OAHK
Trong mặt phẳng (SAC), dựng đường OF song song với SC, khi đó OF là đường trung bình tam giác SAC
$\left\{ \begin{array}{l}
SC \bot \left( {AHK} \right)\\
OF\parallel SC
\end{array} \right. \Rightarrow OF \bot \left( {AHK} \right)$
Trong mặt phẳng (SAC), $OF \cap AN = I$
$ \Rightarrow OI \bot \left( {AHK} \right)$ hay OI là đường cao hình chóp OAHK
* Tính OI
Xét tam giác AOF vuông tại A, có AI là đường cao (F là trung điểm SA)
$\frac{1}{{A{I^2}}} = \frac{1}{{A{F^2}}} + \frac{1}{{A{O^2}}} = \frac{2}{{{a^2}}} + \frac{2}{{{a^2}}} \Leftrightarrow A{I^2} = \frac{{{a^2}}}{4} \Leftrightarrow AI = \frac{a}{2}$
Xét tam giác AIO vuông tại I
$I{O^2} = A{O^2} - I{A^2} = \frac{{{a^2}}}{4} \Leftrightarrow IO = \frac{a}{2}$
Bây giờ ta sẽ tính ${V_{OAHK}}$
${V_{OAHK}} = \frac{1}{3}OI.S\Delta AHK = \frac{1}{3}\frac{a}{2}.\frac{{2{a^2}\sqrt 2 }}{9} = \frac{{{a^3}\sqrt 2 }}{{27}}$
Bạn xem lại đáp án thử $\frac{{{a^3}\sqrt 2 }}{{27}}$ mới đúng hình như đáp án của bạn bị nhầm rồi

Mình nhầm ở chỗ chia khối chóp. Mình đã sửa lại rồi. Hì hì

* Xác định điểm N: Trong mặt phẳng (SAD), từ M vẽ đường thẳng song song với BC cắt SD tại N
Góc Giữa \[\left[ {\widehat{SB,\left( {ABCD} \right)}} \right] = \left[ {\widehat{SB,AB}} \right] = \widehat{SBA} = {60^0}\]
\[\tan \left( {\widehat{SBA}} \right) = \tan {60^0} = \frac{{SA}}{{AB}} = \sqrt 3 \Leftrightarrow SA = a\sqrt 3 \]
\[ \Rightarrow SM = SA - AM = a\sqrt 3 - \frac{{a\sqrt 3 }}{3} = \frac{{2a\sqrt 3 }}{3}\]
Ta có MN song song với AD. Theo định lý Talet đảo ta có tỉ số:
\[\frac{{SM}}{{SA}} = \frac{{SN}}{{SD}} = \frac{{2a\sqrt 3 }}{{3a\sqrt 3 }} = \frac{2}{3}\]
Thể tích hình chóp S.ABCD: \[{V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}a\sqrt 3 .2{a^2} = \frac{{2{a^3}\sqrt 3 }}{3}\]
Ta sẽ sử dụng phương pháp tính thể tích bằng phương pháp tỉ số
Ta có \[{V_{S.ABCD}} = 2{V_{S.ABC}} = 2{V_{S.ACD}}\]
\[\begin{array}{l}
\frac{{{V_{S.BCNM}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.BCM}} + {V_{SMCN}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.BCM}} + {V_{SMCN}}}}{{2{V_{S.ABC}}}} = \frac{{{V_{S.BCM}}}}{{2{V_{S.ABC}}}} + \frac{{{V_{S.MCN}}}}{{2{V_{S.ACD}}}} \\
= \frac{1}{2}\frac{{SB}}{{SB}}.\frac{{SC}}{{SC}}.\frac{{SM}}{{SA}} + \frac{1}{2}\frac{{SC}}{{SC}}.\frac{{SN}}{{SD}}.\frac{{SM}}{{SA}} = \frac{1}{2}.\frac{2}{3} + \frac{1}{2}.\frac{2}{3}.\frac{2}{3} = \frac{5}{9} \\
\Leftrightarrow {V_{S.BCNM}} = \frac{5}{9}{V_{S.ABCD}} = \frac{5}{9}.\frac{{2{a^3}\sqrt 3 }}{3} = \frac{{10{a^3}\sqrt 3 }}{{27}} \\
\end{array}\]

Cho \[a > b > 0\]. Chứng minh rằng phương trình \[\left( {\frac{{{a^3}}}{{{b^2}}} - a + \frac{1}{{{a^2}}}} \right){x^2} + b\left( {{b^2} - 1} \right)x - 1 = 0\] có nghiệm thuộc \[\left( {0;1} \right)\]

\[\mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {2n - 1} \right)\sqrt {2n + 3} }}{{\sqrt {{n^4} + {n^2} + 2} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{\left( {2n - 1} \right)\sqrt {2n + 3} }}{{{n^2}}}}}{{\frac{{\sqrt {{n^4} + {n^2} + 2} }}{{{n^2}}}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{\left( {2n - 1} \right)}}{n}.\frac{{\sqrt {2n + 3} }}{n}}}{{\frac{{\sqrt {{n^4} + {n^2} + 2} }}{{{n^2}}}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {2 - \frac{1}{n}} \right)\sqrt {\frac{2}{n} + \frac{3}{{{n^2}}}} }}{{\sqrt {1 + \frac{1}{{{n^2}}} + \frac{2}{{{n^4}}}} }} = \frac{0}{1} = 0\]

Giải hệ phương trình
Bài 1:
\[\left\{ \begin{array}{l}
4xy + 4\left( {{x^2} + {y^2}} \right) + \frac{3}{{{{\left( {x + y} \right)}^2}}} = 7 \\
2x + \frac{1}{{x + y}} = 3 \\
\end{array} \right.\]

Bài 2:
\[\left\{ \begin{array}{l}
2x + 3y = {x^2} + 3xy + {y^2} \\
{x^2} + 2{y^2} = x + 2y \\
\end{array} \right.\]

Bài 3:

\[\left\{ \begin{array}{l}
2{x^2}{y^2} + {x^2} + 2x = 2 \\
2{x^2}y - {x^2}{y^2} + 2xy = 1 \\
\end{array} \right.\]

Bạn Xusinst giải phương trình cuối hơi rườm rà. Mình xin giải như thế này nha

Do x=0 không là nghiệm của hệ nên hệ phương trình tương đương với
\[\left\{ \begin{array}{l}
\frac{8}{{{x^3}}} - 3y = 2 \\
{y^3} - 3.\frac{2}{x} = 2 \\
\end{array} \right.\]
Đặt \[u = \frac{2}{x}\] ta được phương trình tương đương sau
\[\left\{ \begin{array}{l}
{u^3} - 3y = 2 \\
{y^3} - 3u = 2 \\
\end{array} \right.\]
Từ vế theo vế ta được:
\[\begin{array}{l}
{u^3} - {y^3} + 3\left( {u - y} \right) = 0 \Leftrightarrow \left( {u - y} \right)\left( {{u^2} + uy + {y^2} + 3} \right) = 0 \\
\Leftrightarrow \left( {u - y} \right)\left( {{u^2} + uy + \frac{{{y^2}}}{4} + \frac{{3{y^2}}}{4} + 3} \right) = 0 \\
\Leftrightarrow \left( {u - y} \right)\left[ {{{\left( {u + \frac{y}{2}} \right)}^2} + \frac{{3{y^2}}}{4} + 3} \right] = 0 \\
\end{array}\]
Rõ ràng \[{{{\left( {u + \frac{y}{2}} \right)}^2} + \frac{{3{y^2}}}{4} + 3 \ne 0}\]
Do đó \[u - y = 0\]
\[ \Rightarrow {u^3} - 3u - 2 = 0 \Rightarrow \left[ \begin{array}{l}
u = - 1 \Rightarrow y = - 1 \\
u = 2 \Rightarrow y = 2 \\
\end{array} \right.\]
* Với u=-1
\[\frac{2}{x} = - 1 \Leftrightarrow x = - 2 \Rightarrow y = - 1\]
* Với u=2
\[\frac{2}{x} = 2 \Leftrightarrow x = 1 \Rightarrow y = 2\]
Vậy nghiệm hệ phương trình là \[\left( { - 2, - 1} \right);\left( {1,2} \right)\]

Gọi N là trung điểm AD
Trong mặt phẳng (SBN). MG và BN không song song với nhau nên MG và BN cắt nhau tại điểm E
$ \Rightarrow MG \cap BN = E$
$ \Rightarrow \left\{ \begin{array}{l}
E \in MG \\
E \in BN \subset \left( {ABCD} \right) \\
\end{array} \right. \Rightarrow MG \cap \left( {ABCD} \right) = E$





Trong mặt phẳng (ABCD), $BN \cap AC = K$
$ \Rightarrow \left( {SAC} \right) \cap \left( {SBN} \right) = SK$
Trong mặt phẳng (SBN), $MG \cap SK = H$
$ \Rightarrow \left\{ \begin{array}{l}
H \in MG \\
H \in SK \subset \left( {SAC} \right) \\
\end{array} \right. \Rightarrow MG \cap \left( {SAC} \right) = H$

b.


* chứng minh SA song song với (MPQ)
PM là đường trung bình của tam giác SAB nên $PM\parallel SA$

$\left\{ \begin{array}{l}
SA \not\subset \left( {MPQ} \right) \\
SA\parallel MP \\
MP \subset \left( {MPQ} \right) \\
\end{array} \right. \Rightarrow SA\parallel \left( {MPQ} \right)$


* SD song song (MNQ)
Rõ ràng 3 đường thẩng AC, BD, PQ đồng qui tại trung điểm O
Trong tam giác SBD, OM là đường trung bình nên $OM\parallel SD$

$\left\{ \begin{array}{l}
SD \not\subset \left( {MPQ} \right) \\
SD\parallel OM \\
OM \subset \left( {MPQ} \right) \\
\end{array} \right. \Rightarrow SD\parallel \left( {MPQ} \right)$

c. tìm giao tuyến của 2 mặt phẳng (SAQ) và (MNP)

Gọi J là giao điểm của PN và AQ
Rõ ràng ta có:
$\left\{ \begin{array}{l}
J \in PN \subset \left( {MNP} \right) \\
J \in AQ \subset \left( {SAQ} \right) \\
\end{array} \right. \Rightarrow \left( {MNP} \right) \cap \left( {SAQ} \right) = \left\{ J \right\}{\rm{ }}$
Lại có
$\left\{ \begin{array}{l}
PM\parallel SA \\
PM \subset \left( {PMN} \right);SA \subset \left( {SAQ} \right) \\
\end{array} \right.$
Theo định lý về giao tuyến thì giao tuyến của (PMN) và (SAQ) là đường thẳng đi qua J đồng thời song song với SA, PM và cắt SQ tại F
$ \Rightarrow \left( {MNP} \right) \cap \left( {SAQ} \right) = JF$

Bạn E.Galois sai \[t = \sqrt {2x + 1} \Rightarrow tdt = dx\]
Bài toán trên cũng có thể giải như sau:
\[\int\limits_0^4 {\dfrac{{4x - 1}}{{\sqrt {2x + 1} + 2}}} dx\]
Đặt \[t = \sqrt {2x + 1} + 2 \Leftrightarrow t - 2 = \sqrt {2x + 1} \]
\[ \Leftrightarrow {\left( {t - 2} \right)^2} - 1 = 2x\]
\[ \Leftrightarrow 4x = 2{\left( {t - 2} \right)^2} - 2 \Leftrightarrow 4x - 1 = 2{\left( {t - 2} \right)^2} - 3\]
\[\begin{array}{l}
\Rightarrow \left\{ \begin{array}{l}
\sqrt {2x + 1} + 2 = t \\
4x - 1 = 2{\left( {t - 2} \right)^2} - 3 \\
\end{array} \right. \\
dt = \dfrac{1}{{\sqrt {2x + 1} }}dx \Leftrightarrow \sqrt {2x + 1} dt = dx \Leftrightarrow \left( {t - 2} \right)dt = dx \\
\end{array}\]
Đổi cận
\[\begin{array}{l}
x = 0 \Rightarrow t = 3 \\
x = 4 \Rightarrow t = 5 \\
\end{array}\]\[\begin{array}{l}
\int\limits_3^5 {\dfrac{{2{{\left( {t - 2} \right)}^2} - 3}}{t}} \left( {t - 2} \right)dt = \int\limits_3^5 {\dfrac{{2{{\left( {t - 2} \right)}^3} - 3\left( {t - 2} \right)}}{t}} dt \\
\int\limits_3^5 {\dfrac{{2\left( {{t^3} - 6{t^2} + 12t - 8} \right) - 3t + 6}}{t}dt} = \int\limits_3^5 {\dfrac{{2{t^3} - 12{t^2} + 21t - 10}}{t}dt} \\
= \int\limits_3^5 {\left( {2{t^2} - 12t + 21 - 10\dfrac{1}{t}} \right)dt} \\
= \left( {2\dfrac{{{t^3}}}{3} - 12\dfrac{{{t^2}}}{2} + 21t - 10\ln t} \right)_3^5 \\
= \left( {\dfrac{{250}}{3} - 150 + 105 - 10\ln 5} \right) - \left( {18 - 54 + 63 - 10\ln 3} \right) \\
= \dfrac{{34}}{3} + 10\ln \dfrac{3}{5} \\
\end{array}\]

\[y = {x^2} + 4x - 3\]
Tập xác định D=R
\[\begin{array}{l}
y' = 2x + 4 \\
y' = 0 \Leftrightarrow 2x + 4 = 0 \Leftrightarrow x = - 2 \\
\end{array}\]
\[\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} + 4x - 3} \right) = + \infty \\
\mathop {\lim }\limits_{x \to + \infty } \left( {{x^2} + 4x - 3} \right) = + \infty \\
\end{array}\]
Bảng biến thiên

Đồ thị đạt giá trị cực tiểu tại (-2;-7)
Đồ thị hàm số

b) Phương trình hoành độ giao điểm của (P) và (d) là
\[\begin{array}{l}
{x^2} + 4x - 3 = - x + 3 \\
\Leftrightarrow {x^2} + 5x - 6 = 0 \\
\Leftrightarrow \left[ \begin{array}{l}
x = 1 \Rightarrow y = 2 \\
x = - 6 \Rightarrow y = 9 \\
\end{array} \right. \\
\end{array}\]
Vậy tọa đô giao điểm của (P) và (d) là \[A\left( {1;2} \right);B\left( { - 6;9} \right)\]
c) Tìm m
Phương trình hoành độ giao điểm của (P) và (d) là
\[{x^2} + 4x - 3 = mx - 2\]
\[ \Leftrightarrow {x^2} + \left( {4 - m} \right)x - 1 = 0\]
Để (P) và (d) có 1 điểm chung thì \[\Delta = 0\]
Ta có \[\Delta = {\left( {4 - m} \right)^2} + 4 > 0,\forall m\]
Vậy không có giá trị nào của m để (P) và (d) có 1 điểm chung