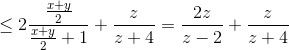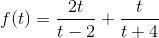có thể giúp e biến đổi chỗ này không em biến đổi mãi mà không ra
Do x + 1 > 0, y + 1 > 0, $\Rightarrow \frac{x+y}{2}+1>0$. Ta có:
$\frac{x}{x+1}+\frac{y}{y+1}\leq 2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}$
$\Leftrightarrow \frac{xy+x+xy+y}{(x+1)(y+1)}\leq \frac{2(x+y)}{x+y+2}$
$\Leftrightarrow (2xy+x+y)(x+y+2)\leq 2(x+y)(xy+x+y+1)$
$\Leftrightarrow 2xy(x+y)+(x+y)^2+4xy+2(x+y)\leq 2xy(x+y)+2(x+y)^2+2(x+y)$
$\Leftrightarrow 4xy\leq (x+y)^2\Leftrightarrow (x-y)^2\geq 0$
- I Love MC yêu thích


 Tìm kiếm
Tìm kiếm Nam
Nam