Bài 1: CMR: nếu a, b là các số nguyên thỏa mãn : $\ 2a^{2} $ + a = $\ 3b^{2} $ +b thì a-b và 2a+ 2b + 1 là những số chính phương.
Bài 2: Cho A= 2+ 2$\sqrt{12n^{2}+1} $ là số nguyên với n $\in $ N thì A là SCP.
Bài 4: a) CM tích của tám số tự nhiên liên tiếp chia hết cho 128
b) Với n $\in $ N, CM: M=n(n+1)(n+2)...(n+7)+7! không biểu diễn được duới dạng tổng của 2 SCP
Bài 5: Cho x,y,z $\in $ N, nguyên tố cùng nhau từng đôi một thỏa mãn $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z} $. Hỏi x+y có phải là số chính phương ko?
Bài 6: Tìm số có 2 chữ số ab sao cho trong bốn mệnh đề sau có 2 mệnh đề đúng, 2 mệnh đề sai:
a) ab $\vdots $ 5
b) ab$\vdots $ 23
c) ab + 7 là SCP
d) ab - 10 là SCP
Bài 7: Cho d là một số nguyên dương $\neq $ 2,5,13.CMR trong tâp hợp { 2,3,13,d} có thể tìm dược h số phân biệt a và b sao cho ab-1 không phải SCP
Bài 8: CMR có tể tìm được số có dạng 19971997...199700...0 $\vdots$ 1998
Bài 9: Cho $\ x_{1} , x_{2}$ là hai nghiệm của pt: $\x^{2} -2x -1=0$. CM $\ x_{1}^{2k} +x_{2}^{2k} +2 $ là SCP với mọi số tự nhiên chẵn k
Bài 10: Tìm số nguyên n sao cho $\ 3^{n} +427$ là SCP
p/s: tính từ hôm nay post bài là thứ 2 thì mình rất mong đến sang thứ 5 thì các bạn đã giúp mình > 5 bài !! Okie?
zzz.chelsea.zzz
Thống kê
- Nhóm: Thành viên
- Bài viết: 96
- Lượt xem: 3308
- Danh hiệu: Hạ sĩ
- Tuổi: 27 tuổi
- Ngày sinh: Tháng mười 21, 1996
-
Giới tính
 Nam
Nam
0
Trung bình
Công cụ người dùng
Lần ghé thăm cuối
Bài tập số chính phương( kỳ cuối)
28-02-2011 - 20:41
bài tập về số chính phương
21-02-2011 - 17:09
dạng bài này có một số bài có thể mò ra kết quả  nhưng tớ mong bạn nào làm được có thể trình bày cách làm:) ko chỉ cho tớ mà cho các bạn # nữa
nhưng tớ mong bạn nào làm được có thể trình bày cách làm:) ko chỉ cho tớ mà cho các bạn # nữa 
Bài 1
a) Tìm số tự nhiên n ( n> 0) sao cho tổng 1! +2! +3! + ..... + n! là một số chính phương
b) Tìm số chính phương abcd và dcba sao cho dcba chia hết cho abcd ( abcd và dcba là một số có 4 chữ số! Mình không biết viết gạch ngang trên đầu thế nào thông cảm )
thông cảm )
Bài 2: Tìm ab biết 2.ab + 1 và 3.ab +1 đều là ssos chính phương ( ab là 1 số có 2 chữ số, chú thích như bài 1b)
Bài 3: Tìm số tự nhiên n sao cho ( với n đạt giá trị nhỏ nhất, mỗi phần là 1 bài # nhau)
a) $ n^{2} + 65 $ là SCP
b) $ n^{2} + n + 91 $ là SCP
c)(n+1)(2n+1) chia hết cho 6 và là một SCP
d) $ 2^{8} + 2^{11} + 2^{n} $ là một SCP
bài 4: Tìm số nguyên lớn nhất n sao cho số T = $ 4^{31} + 4^{1020} + 4^{n} $ là SCP
bài 5: CMR: $ 2^{2p} + 2^{2q} $ ko thể là SCP với p,q là số tự nhiên
bài 6: Tím số tự nhiên n sao cho $ 2^{n} + 153 $ là SCP
bài 7: CMR: tổng các bình phương của m số tự nhiên liên tiếp không thể là 1 SCP với m thuộc {3;4;5;6}
bài 8: Cho m, n là hai số tự nhiên thỏa mãn: m/n = 1- (1/2)+(1/3)-(1/4)+.....+(1/1229)-(1/1330)+(1/1331)
CMR m chia hết cho 1997
bài 9: Tìm số nguyên dương nhỏ nhất thỏa mãn các điều kiện sau: Một phần hai số đó là số chính phương, một phần ba số đó là lập phương của một số nguyên; một phần năm số đó là lũy thừ bậc năm của một số nguyên
Bài 1
a) Tìm số tự nhiên n ( n> 0) sao cho tổng 1! +2! +3! + ..... + n! là một số chính phương
b) Tìm số chính phương abcd và dcba sao cho dcba chia hết cho abcd ( abcd và dcba là một số có 4 chữ số! Mình không biết viết gạch ngang trên đầu thế nào
Bài 2: Tìm ab biết 2.ab + 1 và 3.ab +1 đều là ssos chính phương ( ab là 1 số có 2 chữ số, chú thích như bài 1b)
Bài 3: Tìm số tự nhiên n sao cho ( với n đạt giá trị nhỏ nhất, mỗi phần là 1 bài # nhau)
a) $ n^{2} + 65 $ là SCP
b) $ n^{2} + n + 91 $ là SCP
c)(n+1)(2n+1) chia hết cho 6 và là một SCP
d) $ 2^{8} + 2^{11} + 2^{n} $ là một SCP
bài 4: Tìm số nguyên lớn nhất n sao cho số T = $ 4^{31} + 4^{1020} + 4^{n} $ là SCP
bài 5: CMR: $ 2^{2p} + 2^{2q} $ ko thể là SCP với p,q là số tự nhiên
bài 6: Tím số tự nhiên n sao cho $ 2^{n} + 153 $ là SCP
bài 7: CMR: tổng các bình phương của m số tự nhiên liên tiếp không thể là 1 SCP với m thuộc {3;4;5;6}
bài 8: Cho m, n là hai số tự nhiên thỏa mãn: m/n = 1- (1/2)+(1/3)-(1/4)+.....+(1/1229)-(1/1330)+(1/1331)
CMR m chia hết cho 1997
bài 9: Tìm số nguyên dương nhỏ nhất thỏa mãn các điều kiện sau: Một phần hai số đó là số chính phương, một phần ba số đó là lập phương của một số nguyên; một phần năm số đó là lũy thừ bậc năm của một số nguyên
toán tổ hợp
15-02-2011 - 20:55
Bài 1: Trên biên của hình chữ nhật ABCD, ta lấy M. Hãy tìm đường đi ngắn nhất xuất phát từ M và trở về M có điểm chung với tất cả các cạnh của hình chữ nhật.
Bài 2: CMR một đa giác bất kỳ có chu vi bằng 2a có thể phủ kín bằng một hình tròn có đường kính bằng a.
Bài 4: b) Cho một tờ giấy hình vuông có cạnh bằng a. Tìm giá trị nhỏ nhất của a để có thể cắt được tờ giấy đó năm hình tròn có bán kính bằng 1
a) Cho 1 tờ giấy hình vuông có cạnh bằng 5. CMR có thể cắt được từ tờ giấy đó 5 hình tròn có bán kính bằng 1.
Bài 2: CMR một đa giác bất kỳ có chu vi bằng 2a có thể phủ kín bằng một hình tròn có đường kính bằng a.
Bài 4: b) Cho một tờ giấy hình vuông có cạnh bằng a. Tìm giá trị nhỏ nhất của a để có thể cắt được tờ giấy đó năm hình tròn có bán kính bằng 1
a) Cho 1 tờ giấy hình vuông có cạnh bằng 5. CMR có thể cắt được từ tờ giấy đó 5 hình tròn có bán kính bằng 1.
số nguyên tố - hợp số
14-02-2011 - 19:45
Bài 1: Tìm số hữu tỉ a thỏa mãn $a^{2}$ +5a là số tự nhiên và là số chính phương.
Bài 2:
a) Gọi A là tích của 2002 số tự nhiên khác 0 đầu tiên. Ta chia A lần lượt cho 1;2;3;.....;2002 được các thương tương ứng là $A_{1}$ ; $A_{2}$ ; ....; $A_{2002}$ . Chứng minh rằng tổng ( $A_{1}$ + $A_{2}$ +........+ $A_{2002}$ ) Chia hết cho 2003.
b) Cho n là số tự nhiên khác 0 và p sà số nguyên tố lớn hơn 3. Chúng minh rằng trong hai số ( $p^{n}$ + 1) và ( 2$p^{n}$ + 1) có ít nhất một số là hợp số.
( Thi HSG Toán TP. HN 2002)
Bài 3:
a) Chứng minh rằng tích của 4 số tự nhiên liên tiếp rồi cộng với 1 luôn là số chính phương.
b) Tim tất cả các số tự nhiên a và b thỏa mãn A = $a^{4}$ + $b^{4}$ là số nguyên tố.
( THi HSG Toán TP. HN .V1 1998)
Bài 4: Chứng minh rằng với mỗi số nguyên dương n có n số nguyên dương liên tiếp sao cho không có số nào trong n số đó là lũy thừ nguyên của một số nguyên tố
( thi vô địch toán quốc tế -1998 )
Bài 5: Cho a,b,c,d là các số nguyên dương thỏa mãn ab = cd.Chứng minh số A = $a^{n}$ + $b^{n}$ + $c^{n}$ + $d^{n}$ là hợp số với mọi n nguyên dương.
Bài 6: cho số tự nhiên n > 1 và n không chia hết cho 3. Chứng minh rằng số A= $ 3^{2n}$ + $3_{n}$ + 1 là hợp số.
Bài 7: Tìm 7 số nguyên tố sao cho tích của chúng bằng tổng các lũy thừ bậc 6 của 7 sô đó
Bài 2:
a) Gọi A là tích của 2002 số tự nhiên khác 0 đầu tiên. Ta chia A lần lượt cho 1;2;3;.....;2002 được các thương tương ứng là $A_{1}$ ; $A_{2}$ ; ....; $A_{2002}$ . Chứng minh rằng tổng ( $A_{1}$ + $A_{2}$ +........+ $A_{2002}$ ) Chia hết cho 2003.
b) Cho n là số tự nhiên khác 0 và p sà số nguyên tố lớn hơn 3. Chúng minh rằng trong hai số ( $p^{n}$ + 1) và ( 2$p^{n}$ + 1) có ít nhất một số là hợp số.
( Thi HSG Toán TP. HN 2002)
Bài 3:
a) Chứng minh rằng tích của 4 số tự nhiên liên tiếp rồi cộng với 1 luôn là số chính phương.
b) Tim tất cả các số tự nhiên a và b thỏa mãn A = $a^{4}$ + $b^{4}$ là số nguyên tố.
( THi HSG Toán TP. HN .V1 1998)
Bài 4: Chứng minh rằng với mỗi số nguyên dương n có n số nguyên dương liên tiếp sao cho không có số nào trong n số đó là lũy thừ nguyên của một số nguyên tố
( thi vô địch toán quốc tế -1998 )
Bài 5: Cho a,b,c,d là các số nguyên dương thỏa mãn ab = cd.Chứng minh số A = $a^{n}$ + $b^{n}$ + $c^{n}$ + $d^{n}$ là hợp số với mọi n nguyên dương.
Bài 6: cho số tự nhiên n > 1 và n không chia hết cho 3. Chứng minh rằng số A= $ 3^{2n}$ + $3_{n}$ + 1 là hợp số.
Bài 7: Tìm 7 số nguyên tố sao cho tích của chúng bằng tổng các lũy thừ bậc 6 của 7 sô đó
ai làm hộ tui với...
13-01-2011 - 11:35
bài 1: Cho 5 đoạn thẳng a,b,c,d,e trong đó bất cứ 3 đoạn nào cũng lập thành 1 $ \Delta $. CMR: tồn tại 3 đoạn thẳng lập thành một tam giác có 3 góc nhọn( cho biết điều kiện để 3 đoạn thẳng m,n,p lập thành 1 $ \Delta $ có cạnh m đối diện với góc tù là $ \ m^2 > n^2 +p^2 $)
bài 2: CHo 5 điểm ở bên trong một đa giác đều có cạnh 2. CMR trong 5 điểm đó, tồn tại 2 điểm có khoảng cách giữa chúng nhỏ hơn 1.
Bài 3: Bên trong 1 $ \Delta $ đều có cạnh bằng 10 có 45 điểm. CMR tồn tại 1 hình tròn bán kính = 1 chứa ít nhất 3 trong 45 điểm đã cho.
Bài 4: Ở bên trong một đường tròn bán kính = 1 người ta đặt hai $ \Delta $, mỗi $ \Delta $ có diện tích lớn hơn 1. CMR tồn tại 1 điểm nằm bên trong cả hai $ \Delta $
Bài 5: Cho 30 điểm trong mặt phẳng, trong đó không có 3 điểm nào thẳng hàng. CMR có thể vẽ được 10 $ \Delta $ không giao nhau có các đỉnh là các điểm đã cho
Bài 6 : CHo một đa giác lồi có diện tích 24 cm ^2 CMR bao giờ ta cũng vẽ được trong đa giác đó một $ \Delta $ có diện tích không nhỏ hơn 9 $ \ cm^2 $
Bài 7: Bên trong một hình Chữ nhật có kích thước 13cmX14 cm , đặt 10 tấm bìa ngũ giác lồi, diện tích mỗi ngũ giác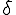 3cm^2 . Chu vi mỗi ngũ giác
3cm^2 . Chu vi mỗi ngũ giác  6 cm. CMR trong hình Chữ Nhật đó tồn tại 1 hình tròn có bán kính 1cm mà ko chờm lên một tấm bìa nào
6 cm. CMR trong hình Chữ Nhật đó tồn tại 1 hình tròn có bán kính 1cm mà ko chờm lên một tấm bìa nào
Bài 8: Bên trong một hình chữ nhật có kích thước 16 X 20, đặt 50 quân cờ hình chữ nhật có kích thước 1X2 CMR: có thể đặt được 1 tấm bìa hình vuông có cạnh =1 và chờm lên 2 quân cờ
bài 2: CHo 5 điểm ở bên trong một đa giác đều có cạnh 2. CMR trong 5 điểm đó, tồn tại 2 điểm có khoảng cách giữa chúng nhỏ hơn 1.
Bài 3: Bên trong 1 $ \Delta $ đều có cạnh bằng 10 có 45 điểm. CMR tồn tại 1 hình tròn bán kính = 1 chứa ít nhất 3 trong 45 điểm đã cho.
Bài 4: Ở bên trong một đường tròn bán kính = 1 người ta đặt hai $ \Delta $, mỗi $ \Delta $ có diện tích lớn hơn 1. CMR tồn tại 1 điểm nằm bên trong cả hai $ \Delta $
Bài 5: Cho 30 điểm trong mặt phẳng, trong đó không có 3 điểm nào thẳng hàng. CMR có thể vẽ được 10 $ \Delta $ không giao nhau có các đỉnh là các điểm đã cho
Bài 6 : CHo một đa giác lồi có diện tích 24 cm ^2 CMR bao giờ ta cũng vẽ được trong đa giác đó một $ \Delta $ có diện tích không nhỏ hơn 9 $ \ cm^2 $
Bài 7: Bên trong một hình Chữ nhật có kích thước 13cmX14 cm , đặt 10 tấm bìa ngũ giác lồi, diện tích mỗi ngũ giác
Bài 8: Bên trong một hình chữ nhật có kích thước 16 X 20, đặt 50 quân cờ hình chữ nhật có kích thước 1X2 CMR: có thể đặt được 1 tấm bìa hình vuông có cạnh =1 và chờm lên 2 quân cờ
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Chủ đề: zzz.chelsea.zzz


 Tìm kiếm
Tìm kiếm







