Zaraki

Như vậy lời giải cho hai bài Tuần 2 tháng 4/2017 đã được đăng tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng và bạn Nguyễn Đức Bảo. Xin trích dẫn lại hai bài toán

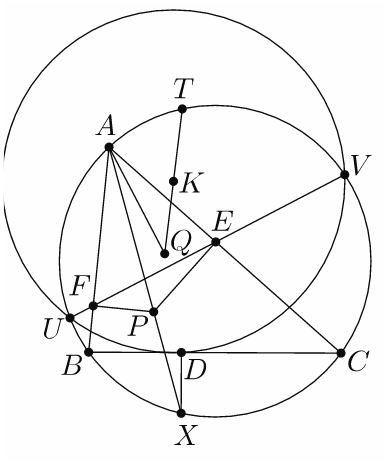
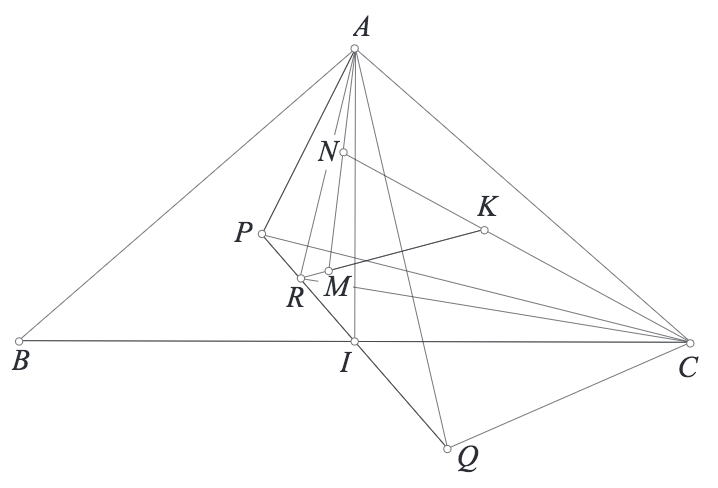
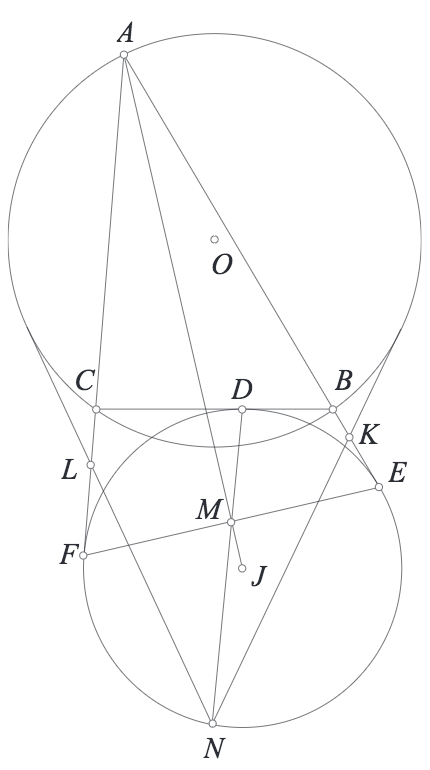
Bài 1. Cho tam giác $ABC$ có $P$ nằm trên phân giác gód $\angle BAC$. $D,E,F$ là hình chiếu của $P$ lin $BC,CA,AB$. $AP$ cắt đường tròn $(PBC)$ tại $Q$ khác $P$. $DP$ cắt đường tròn $(DEF)$ tại $K$ khác $D$. $L$ đối xứng $K$ qua $EF$. $AL$ cắt $BC$ tại $R$. Chứng minh rằng đường thẳng $QR$ đi qua điểm cố định khi $P$ thay đổi.

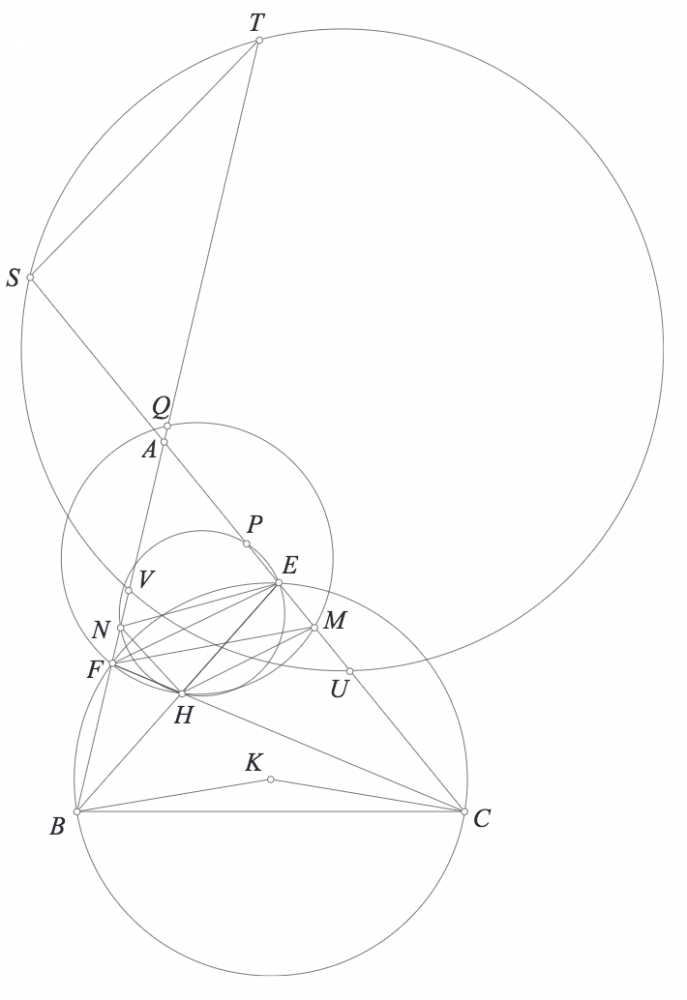
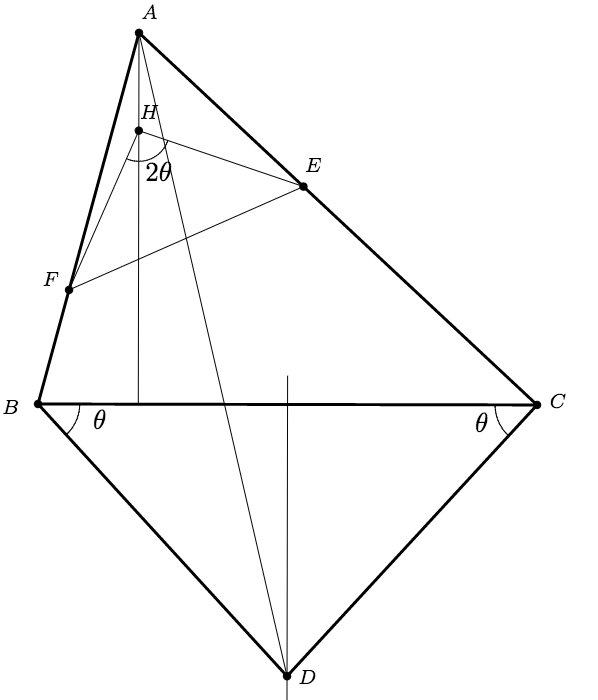
Bài 2. Cho tam giác $ABC$, $P$ thuộc đường thẳng cố định. Các đường thẳng qua $P$ lần lượt vuông góc với $CA,AB$ cắt các đường thẳng $AB,AC$ theo thứ tự tại $E,F$. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $PEF$ thuộc một đường thẳng cố định.

Như vậy lời giải cho hai bài Tuần 4 tháng 3/2017 đã được đưa tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng và anh Nguyễn Tiến Dũng. Xin trích dẫn lại hai bài toán:

Bài 1. Cho tam giác $ABC$ nhọn có đường cao $AD,BE,CF$ đồng quy tại $H$ và có tâm ngoại tiếp $O$. Đường tròm đường kính $AO$ cắt đường tròn ngoại tiếp tam giác $BOC$ tại $K$ khác $O$ và cắt đường tròn ngoại tiếp tam giác $DKH$ tại $L$ khác $K$. Đường tròn ngoại tiếp tam giác $DKH$ cắt $BC$ tại $G$ khác $D$. $GE,GF$ lần lượt cắt $DF,DE$ tại $M,N$. Chứng minh rằng $MN \parallel GL$.

Bài 2. Cho tam giác $ABC$ cố định và điểm $P$ thay đổi sao cho $\frac{PB}{PC} =\frac{AB}{AC}$. Dựng hai hình chứ nhật bằng nhau cùng ngược hướng với tam giác $ABC$ là $PBDE$ và $PGCF$. Chứng minh rằng khi $P$ thay đổi thì đường tròn nối tâm hai hình chữ nhật luôn đi qua một điểm cố định.

Thực ra bài 1 không khó nhưng có lẽ cách phát biểu nó làm các bạn hơi hoang mang. Dĩ nhiên là phải phản chứng, giả sử là 2 con kiến bất kì đều gặp nhau. Vận tốc của 2 con kiến bất kì khác nhau nên dĩ nhiên nếu 2 con cùng xuất phát ở 1 lỗ và ở cùng thời điểm thì chả bao giờ gặp nhau cả ( đi cùng chiều thì ko gặp rồi mà ngược chiều thì càng chẳng bao giờ gặp). 2017 con kiến mà 44 lỗ thì có 45 con cùng chuồng. Và dĩ nhiên để đáp ứng điều kiện phản chứng thì 45 con này xuất phát thời điểm khác nhau, cộng thêm cái thời điểm của cái con xuất phát trễ nhất nó chui vào lỗ nữa thì phải có ít nhất 46 thời điểm. Mâu thuẫn!

 

Dựa vào lời giải của anh Karl thì ta có thể làm mạnh kết quả một tí: bài toán đúng cho $|T| \le 46$.

Có $2017=37+44 \cdot 45$ nên tồn tại lỗ có $46$ con kiến xuất phát. Nếu $46$ con kiến này xuất phát tại thời điểm khác nhau + thời điểm con kiến chậm trở về lỗ nhất trong $46$ con này thì sẽ có $47$ thời điểm, mâu thuẫn.

giả sử thêz thì khi 2 con kiến chui cùng từ một lỗ thì có tính là nó sẽ gặp nhau tại cái lỗ đó không anh ?

Chắc là không, vì nếu mà như dungxibo123 nói thì khi đó sẽ có trường hợp tất cả các con kiến đều gặp nhau khi cùng xuất phát tại 1 lỗ chung, dẫn đến bài toán sai.

Lời giải trước của mình sai nên xin đề xuất lời giải khác cho bài 6, thêm thắt chút về hướng giải, suy nghĩ:

Gọi điều kiện $a_i-a_{i+1} \not\equiv a_{j}-a_{j+1} \pmod{2n+1}$ là điều kiện (*).

Nhận thấy rằng nếu xây dựng được $a_1, \ldots, a_n$ thì ta xây dựng được cả $2n$ số. Ta muốn đơn giản hoá phép xây dựng càng nhiều càng tốt, do đó ta sẽ thử chỉ gán các số $1,2, \ldots ,n$ cho $a_1, \ldots, a_n$ và không quan tâm đến $n+1, \ldots, 2n$. Nếu như thế thì $-n+1 \le a_i-a_{i+1} \le n-1$ với mọi $1 \le i<n$. Do đó chỉ việc xây dựng cho dãy sao cho $a_i-a_{i+1} \ne a_{j}-a_{j+1}$ cho $1 \le i<j<n$ là ta hoàn toàn có thể đảm bảo điều kiện $a_i-a_{i+1} \not\equiv a_j-a_{j+1} \pmod{2n+1}$ cho $1 \le i<j<n$. Điều này tương đương với việc phải đảm bảo $|a_1-a_2|,|a_2-a_3|, \ldots, |a_{n-1}-a_n|$ là hoán vị của $1,2, \ldots , n-1$.

Nếu áp dụng ý tưởng xây dựng trên thì đối với $2n >i \ge n$ thì $a_{i}-a_{i+1}=a_{i+1-n}-a_{i-n}$ nên nếu dãy $a_1, \ldots , a_n$ thoả mãn điều kiện (*) thì dãy $a_{n+1}, \ldots, a_{2n}$ cũng thoả mãn. Tuy nhiên, cần để ý tới $j=2n$ hay $a_{2n}-a_{2n+1}=2n+1-a_{n}-a_1$. Chú ý rằng ta không thể kẹp $2n+1-a_n-a_1$ như đã làm ở trên nên việc thoả mãn điều kiện sẽ gây khó khăn. Thay vào đó, ta có thể chọn trước giá trị cho $a_n,a_1$ để đảm bảo $2n+1-a_n-a_1 \not\equiv a_i-a_{i+1} \pmod{2n+1}$ với mọi $1 \le i<2n$. Do $a_i-a_{i+1} \in \{ \pm 1, \pm 2, \ldots , \pm(n-1) \}$ nên để $2n+1-a_n-a_1 \not\equiv a_i-a_{i+1} \pmod{2n+1}$ vớ mọi $1 \le i<2n$ thì $2n+1-a_n-a_1 \in \{ n,n+1 \}$ hay $a_n+a_1 \in \{n,n+1 \}$.

Qua bước lập luận trên, bài toán 6 có thể đưa về việc xây dựng một hoán vị của $1,2, \ldots , n$ là $a_1,a_2, \ldots, a_n$ sao cho $|a_i-a_{i+1}| \ne |a_j-a_{j+1}|$ với mọi $1 \le i<j<n$ và $a_1+a_n \in \{n,n+1\}$. Đến đây, để cho dễ hình dung, hãy tưởng tượng các số $1,2, \ldots, n$ được viết theo thứ tự từ trái qua phải, một con cóc bắt đầu ở vị trí số $a_1$ và nhảy với khoảng cách $|a_1-a_2|$ tới vị trí $a_2$ và cứ thế cho đến khi nó đến vị trí $a_n$. Thử thách của ta là làm sao cho con cóc có thể

+) Đi qua hết các vị trí $1, \ldots , n$ mỗi vị trí đúng $1$ lần.

+) Nhảy với khoảng cách nhảy $|a_i-a_{i+1}|$ khác nhau tại mỗi lần.

+) Bắt đầu tại $a_1$ và kết thúc tại $a_n$ sao cho $a_1+a_n \in \{n,n+1 \}$.

Trường hợp 1. Nếu thì $n=4k+1$: 

Con cóc bắt đầu đi từ vị trí $k+1$ và thực hiện như sau: (dấu ngoặc mình thêm vào chỉ để cho dễ hình dung quy luật dãy):

$(k+1, 3k+2), (k,3k+3),(k-1, 3k+4), \ldots , (k-i,3k+(i+3)), \ldots, ( k-(k-2),3k+(k+1)), 1$

Khoảng cách con cóc nhảy cho mỗi bước này là $2k+1,2k+2, \ldots, 4k$.

Ta nhận thấy lúc này, con cóc chỉ còn các vị trí $k+2, \ldots , 3k,3k+1$ là chưa nhảy tới và còn khoảng cách $1,2, \ldots, 2k$ là chưa dùng để nhảy. Con cóc lúc này bắt đầu tại $1$ và có thể nhảy như sau:

$1,\color{blue} {2k+1},\color{red} {2k+2},\color{blue}{2k},\color{red} {2k+3},\color{blue} {2k-1},\color{red} {2k+4}, \ldots,  \color{blue} {k+2} ,\color{red} {3k+1}$

Như vậy con cóc đã nhảy qua hết $n=4k+1$ vị trí và dùng hết $4k$ khoảng cách nhảy, bắt đầu tại $a_1=k+1$ và kết thúc với $a_n=3k+1$ với $(k+1)+(3k+1)=n+1$. Một ví dụ con cóc nhảy cho $n=9$:

Trường hợp 2. Nếu $n=4k+3$:

$(k+1,3k+3),(k,3k+4), \ldots , (k-(k-2),3k+(k+2))=(2,4k+2),(1,4k+3)$.

Như vậy con cóc còn các vị trí $k+2, \ldots , 3k+2$ chưa nhảy tới và khoảng cách nhảy $1,2 \ldots, 2k+1$ chưa dùng. Bước tiếp theo, con cóc có thể nhảy như sau, bắt đầu từ $4k+3$:

$4k+3,\color{blue}{2k+2},\color{red}{2k+1}, \color{blue}{2k+3}, \color{red}{2k}, \ldots, \color{blue}{3k+1},\color{red}{k+2},\color{blue}{3k+2}$.

Bước nhảy trên thoả mãn đề bài. Con cóc bắt đầu với $a_1=k+1$ và kết thúc với $a_n=3k+2$ với $a_1+a_n=4k+3=n$.

Trường hợp 3. Nếu $n=4k$:

$(k,3k+1),(k-1,3k+2), \ldots (k-(k-1),3k+k)=(1,4k)$.

Như vậy, con cóc còn các vị trí $k+1, \ldots, 3k$ chưa nhảy tới và khoảng cách nhảy $1,2 \ldots, 2k$ chưa dùng. Con cóc bước tiếp theo có thể nhảy như sau, bắt đầu từ vị trí $4k$:

$4k, \color{blue}{2k},\color{red}{2k+1},\color{blue}{2k-1}, \color{red}{2k+2}, \ldots, \color{blue}{k+1},\color{red}{3k}$

Con cóc hoàn thành nhiệm vụ.

Trường hợp 4. Nếu $n=4k+2$: 

$(k+1,3k+3),(k,3k+4), \ldots , (k-(k-2),4k+2),1$.

Như vậy, con cóc còn các vị trí $k+2, \ldots, 3k+2$ chưa nhảy tới và khoảng cách nhảy $1,2 \ldots, 2k+1$ chưa dùng. Con cóc bước tiếp theo có thể nhảy như sau, bắt đầu từ vị trí $1$:
 

$1, \color{blue}{2k+2},\color{red}{2k+1},\color{blue}{2k+3},\color{red}{2k}, \ldots, \color{blue}{k+2},\color{red}{3k+2}$.

Vậy con cóc có thể có các bước nhảy thoả mãn đề bài. Thứ tự vị trí mà con cóc nhảy tới chính là thứ tự của dãy số $a_1, \ldots, a_n$. Như vậy ta đã xây dựng được dãy $a_1, \ldots, a_n$ thoả mãn nên suy ra dãy $a_1, \ldots, a_{2n}$ cũng thoả mãn theo lập luận trên.

Như vậy lời giải cho hai bài toán Tuần 3 tháng 3/2017 đã được đưa tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng Hùng và thầy Nguyễn Lê Phước. Xin trích dẫn lại hai bài toán:
 

Bài 1. Cho tam giác $ABC$ cố định và đường tròn $(K)$ thay đổi đi qua $B,C$ cắt $CA,AB$ tại $E,F$. Gọi $J,L$ lần lượt là tâm ngoại tiếp của các tam giác $ABE,ACF$. $EJ$ cắt $FL$ tại $P$. $Q$ là tâm ngoại tiếp tam giác $KEF$. Chứng minh rằng đường thẳng $PQ$ luôn đi qua một điểm cố định khi $(K)$ thay đổi.

Bài 2. Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$ cố định với $B,C$ cố định và $A$ di chuyển trên $(O)$. $P$ là điểm cố định trên trung trực $BC$. Trên đường thẳng $CA,AB$ lấy các điểm $E,F$ sao cho $PE \parallel AB, PF \parallel AC$. Chứng minh rằng trung trực $EF$ luôn đi qua một điểm cố định khi $A$ di chuyển. 

Lời giải này sai. Minh có đưa ra lời giải khác ở dưới:

Bài 6. Với mỗi số nguyên dương $n$, xét $a_1,a_2, \ldots, a_{2n}$ là hoán vị của $2n$ số nguyên dương đầu tiên. Một hoán vị như thế được gọi là đẹp nếu với mọi $1 \le i < j \le 2n$ thì $a_i+a_{n+i}=2n+1$ và $a_i-a_{i+1}$ không đồng dư với $a_j-a_{j+1}$ theo modulo $2n+1$. Quy ước $a_{2n+1}=a_1$.

a) Với $n=6$, hãy chỉ ra một hoán vị đẹp.
b) Chứng minh rằng với mỗi $n$ nguyên dương thì luôn tồn tại một hoán vị đẹp.

Lời giải. Do $a_i+a_{n+i}=2n+1$ nên ta chỉ việc xây dựng $a_1,a_2, \cdots, a_n$ là đủ. Ta làm như sau:

Với các vị trí lẻ $a_1,a_3, \cdots, $ ta viết các số bắt đầu từ $1$ và tăng dần $1,2,3, \cdots$ (các số được viết cho tới khi không tìm được vị trí lẻ) và với vị trị chẵn $a_2,a_4, \cdots$ ta viết các số bắt đầu từ $n$ theo thứ tự giảm dần $n,n-1,n-2, \ldots$ Khi đó dãy các số $a_1, \cdots , a_n$ sẽ là một hoán vị của $n$ số nguyên dương đầu tiên. Ta sẽ chứng minh rằng trong dãy này, không tồn tại $1\le i<j < n$ sao cho $a_i-a_{i+1} \equiv a_j-a_{j+1} \pmod{2n+1}$. Trước hết, để ý rằng $-n+1 \le a_i-a_{i+1} \le n-1$ với mọi $1 \le i< n$ nên $a_i-a_{i+1} \equiv a_j-a_{j+1} \pmod{2n+1}$ khi và chỉ khi $a_i-a_{i+1}=a_j-a_{j+1}$. Tuy nhiên, không khó để chứng minh bằng quy nạp rằng trong dãy $a_1, \ldots , a_n$, với mọi $1 \le i<n$ thì $a_i-a_{i+1}=(-1)^{i}(n-i)$. Do đó $a_i-a_{i+1} \ne a_j-a_{j+1}$ với mọi $1 \le i<j < n$ hay $a_i-a_{i+1} \not\equiv a_j-a_{j+1} \pmod{2n+1}$ với mọi $1 \le i<j< n$.

Như vậy ta đã xây dựng xong dãy $a_1, \ldots, a_n$ thoả mãn $a_i-a_{i+1}=(-1)^{i}(n-i)$ với mọi $1 \le i<n$. Do đó $a_{i+n}-a_{i+1+n}=a_{i+1}-a_i=(-1)^{i+1}(n-i)$. Từ đây ta suy ra rằng với cách xây dựng trên thì $-n+1 \le a_i-a_{i+1} \le n-1$ với mọi $1 \le i<2n$. Do đó $a_i-a_{i+1} \equiv a_j-a_{j+1} \pmod{2n+1}$ khi và chỉ khi $a_i-a_{j+1}=a_j-a_{j+1}$. Ta đã chứng minh rằng $a_i-a_{i+1} \ne a_j-a_{j+1}$ cho mọi $1 \le i<j<n$ và hoàn toàn tương tự, điều này cũng đúng với $n \le i<j<2n$. Trường hợp còn lại chưa chứng minh là khi $1\le i<n \le j<2n$. Khi đó $a_i-a_{i+1}=a_j-a_{j+1}=a_{j+1-n}-a_{j-n}$ suy ra tồn tại $1 \le i<j<n$ sao cho $a_i-a_{i+1}=-(a_j-a_{j+1})$ mâu thuẫn theo phép xây dựng của dãy $a_1, \ldots , a_n$ cho rằng $|a_i-a_{i+1}|=(n-i)>(n-i-1)=|a_{i+1}-a_{i+2}|$ với mọi $1 \le i \le n-2$.

Vậy, với mọi $1 \le i<j<2n$ thì $a_i-a_{i+1} \not\equiv a_j-a_{j+1} \pmod{2n+1}$. Ta chỉ cần kiểm tra cho trường hợp $j=2n$, tức cần chứng minh $a_{2n}-a_{2n+1}=a_{2n}-a_1 \not\equiv a_i-a_{i+1} \pmod{2n+1}$ (chú ý rằng ta không thể đưa về chứng minh $a_{2n}-a_1 \ne a_i-a_{i+1}$ được vì ta không thể khẳng định $-n+1 \le a_{2n}-a_1 \le n-1$). Để ý rằng $a_{2n} =2n+1-a_n$ và ta theo phép xây dựng trên, ta có thể chứng minh rằng $a_n=\left \lfloor \frac n2 \right \rfloor +1$. Do đó $a_{2n}=2n+1- \left \lfloor \frac n2 \right \rfloor$ nên $a_{2n}-a_1=2n-\left \lfloor \frac n2 \right \rfloor $ suy ra $a_{2n}-a_1 \in \{ n,n+1 \}$. Tuy nhiên $-n+1 \le a_{i}-a_{i+1} \le n-1$ nên không tồn tại $1 \le i <2n$ sao cho $a_i-a_{i+1} \equiv a_{2n}-a_1 \pmod{2n+1}$.

Dãy số xây dựng thoả mãn bài toán.

Nhận xét. Một điểm thú vị là nếu ban đầu ta chọn các vị trí lẻ $a_1,a_3 \ldots$ không phải là $1,2,3, \ldots$ mà lại là $n,n-1, \ldots$, tương tự với vị trí chẵn. Khi đó, ta sẽ dẫn đến việc khó khăn trong chứng minh không tồn tại $i$ sao cho $a_i-a_{i+1} \equiv a_{2n}-a_1 \pmod{2n+1}$. 

Như vậy lời giải cho bài Tuần 2 tháng 3/2017 đã được đưa tại đây kèm theo đó là hai bài toán mới của thầy Hùng và anh Trần Quang Huy. Xin trích dẫn lại bài toán mới:

Bài 1. Cho tam giác $ABC$ và đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ lần lượt tại $E,F$. $BE$ cắt $CF$ tại $H$. $M,N$ lần lượt là trung điểm của $CA,AB$ $U,V$ lần lượt là điểm đối xứng của $E,F$ qua $M,N$. Đường tròn $(EHN),(FHM)$ lần lượt cắt $CA,AB$ tại $P,Q$ khác $E,F$. $S,T$ lần lượt là đối xứng của $C,B$ qua $P,Q$. Chứng minh rằng bốn điểm $U,V,S,T$ cùng thuộc một đường tròn.

Bài 2. Cho các điểm $A,P,Q,K$ sao cho không có ba điểm nào thẳng hàng. Xét họ các tam giác $\{ \triangle AB_iC_i \}_{i=1}^{\infty}$ thoả mãn:

i) $B_i,C_i$ đi qua $K$ với mọi $i$.

ii) $P,Q$ đẳng giác trong $\triangle AB_iC_i$ với mọi $i$.

Chứng minh rằng các đường tròn $\{ (AB_iC_i) \}_{i=1}^{\infty}$ là một họ các đường tròn đồng trục.

Như vậy lời giải cho bài toán Tuần 1 tháng 3/2017 đã được thầy Hùng đưa tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

Cho tam giác $ABC$ cân tại $A$. $P,Q$ đối xứng nhau qua trung điểm $BC$ và $PQ \perp AB$. $K$ là tâm ngoại tiếp tam giác $APQ$ và $AR$ là đường đối trung của tam giác $APQ$. $KR,KC$ cắt phân giác $\angle PAQ$ tại $M,N$. Chứng minh rằng $KM=KN$.

Chuyên mục Mỗi tuần một bài toán cũng sẽ bắt đầu nhận và đăng bài đề nghị từ bạn đọc. Đề đề nghị có thể gửi qua email teamhinhhochsgs[a còng]gmail.com. Xin trích dẫn lại đề đề nghị của tuần này đến từ tác giả Trịnh Huy Vũ, K61 Toán, ĐHKHTN, ĐHQGHN:

Cho tam giác $ABC$. Trên trung trực của đoạn $BC$ lấy điểm $D$ sao cho $\angle DBC= \angle DCB= \theta$ và $A,D$ khác phía so với $BC$. Lấy hai điểm $E,F$ tương ứng nằm trên hai cạnh $CA,AB$ của tam giác $ABC$ sao cho đường thẳng $AD$ đi qua trung điểm của $EF$. Trên trung trực $EF$ lấy điểm $H$ sao cho $\angle EHF=2\theta$ và $A,H$ nằm cùng phía với $EF$. Chứng minh rằng $AH \perp BC$.

Như vậy lời giải cho bài Tuần 4 tháng 2/2017 đã được thầy Hùng đưa tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới

Cho tam giác $ABC$ có tâm ngoại tiếp $(O)$, trực tâm $H$ và điểm Lemoine là $L$. $AO,BO,CO$ lần lượt cắt các đường tròn ngoại tiếp tam giác  $BOC,COA,AOB$ tại $D,E,F$ khác $O$. $X,Y,Z$ là trung điểm $BC,CA,AB$. Trung trực của $AD,BE,CF$ lần lượt cắt $YZ,ZX,XY$ tại $U,V,W$. Chứng minh rằng $U,V,W$ thẳng hàng trên một đường thẳng vuông góc với $HL$.

Như vậy lời giải cho bài Tuần 3 tháng 2/2017 đã được thầy Hùng đưa tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

Cho tam giác $ABC$ có tâm nội tiếp $I$, tâm ngoại tiếp $O$ và tâm bàng tiếp ứng với đỉnh $A$ là $J$. $M,N$ đối xứng với $A$ qua $IB,IC$. $P,Q$ đối xứng với $B,C$ qua $IA$. $JM,JN$ cắt đường thẳng $OI$ tại $E,F$. $PE$ cắt $FB$ tại $S$. $EC$ cắt $FQ$ tại $T$. Chứng minh rằng $S,T,J$ thẳng hàng.

Như vậy lời giải cho bài Tuần 2 tháng 2/2017 đã được thầy Hùng đưa ra tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. $M$ là trung điểm $EF$. $DM$ cắt $(J)$ tại $N$ khác $D$. Trên đoạn $AE,AF$ lần lượt lấy các điểm $K,L$ sao cho $NK,NL$ tiếp xúc $(O)$. Chứng minh rằng tứ giác $AKNL$ ngoại tiếp.

Bạn có thể tìm nhiều mở rộng khác cho định lý Wolstenholme tại đây.

Như vậy là lời giải cho bài Tuần 1 tháng 2 năm 2017 đã được thầy Hùng cho lời giải tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và phân giác $AD$. $K,L$ là tâm ngoại tiếp tam giác $ADB,ADC$. Tiếp tuyến qua $A$ của $(O)$ cắt $BC$ tại $T$. $AK,AL$ cắt $OT$ tại $P,Q$. $E,F$ là hình chiếu của $Q,P$ lên $CA,AB$. $M,N$ là trung điểm của $BC,AM$. $NE,NF$ cắt $BC$ tại $U,V$. Chứng minh rằng tam giác $NUV$ cân.

Em có thấy tại đây có thầy/anh/bác/chú chanhquocnghiem báo là không đăng nhập vào diễn đàn được.