Rayky

Mọi người cho em hỏi bài Bđt các vai trò của các biến x có như nhau không ạ? Từ đó có thể giả sử $x_{n} \geq x_{n-1} \geq ...\geq x_{2} \geq x_{1}$ không ạ? Em làm cách này ra khá đẹp nhưng có đứa bảo vai trò các biến không bình đẳng mà mọi người đều làm cách khác nên em thấy cũng ngờ ngợ. AI giải đáp hộ em cái

@nguyenta98: KHông được vì khi đó $|a_1-a_2|...+|a_n-a_1|$ không còn tổng quát nữa

Bài giải ngày 17/8/2011
Bài 3: Theo cách của isaac_newtons
Ta có :
$ S= \dfrac{1}{2}bcsinA $
$ S^2= \dfrac{1}{4}b^2c^2(1-cos^2A)=\dfrac{1}{4}b^2c^2[1- \dfrac{(b^2+c^2-a^2)^2}{4b^2c^2}] $
$ = \dfrac{1}{16}(2bc + b^2+c^2-a^2)(2bc-b^2-c^2+a^2) = \dfrac{1}{16} [(b+c)^2-a^2][a^2-(b-c)^2]= \dfrac{a+b+c}{2} \dfrac{b+c-a}{2}\dfrac{a-b+c}{2}\dfrac{a+b-c}{2}=p(p-a)(p-b)(p-c) $
vậy $S = \sqrt {p(p - a)(p - b)(p - c)} $

Ngày 18/8/2011 và ngày 19/8/2011
Bài 4: Từ chuyên đề hệ thức tam giác thường
Cho tam giác ABC có ${l_a},{l_b},{l_c}$ là những phân giác trong tam giác ABC. CMR:
$\dfrac{2}{R} \le \dfrac{1}{{{l_a}}} + \dfrac{1}{{{l_b}}} + \dfrac{1}{{{l_c}}} \le \dfrac{1}{r}$

Bài 5: Từ chuyên đề hệ thức tam giác thường
Cho tam giác ABC với các yếu tố độ dài các cạnh là: BC = a, AC = b, AB = c. CMR:
$\forall x,y,z > 0$
$\dfrac{x}{{y + z}}{a^2} + \dfrac{y}{{x + z}}{b^2} + \dfrac{z}{{x + y}}{c^2} \ge 2S\sqrt 3 $
(S ở đây là diện tích tam giác ABC)

P/S: @anh perfectstrong, em vẫn thấy đề như vậy mà X_X Sao lại

Lấy C trên tia DC sao cho C nằm giữa D, N và DN=3CN

được nhỉ khi DC cố định >.>

@perfectstrong: Em năm nay lên lớp 9, còn về số bài thì chắc 1 với 2 thế nào cũng được, tùy hôm. Mà đề bài 3 của anh có đúng không vậy Có gì thành bài 4 nhé anh X_X
17/8/2011
Bài 3:
Chứng minh công thức Hê-rông cho tam giác ABC:
$S = \sqrt {p(p - a)(p - b)(p - c)} $

Bài giải 16/8/2011
Bài 1: Theo cách của Perfectstrong

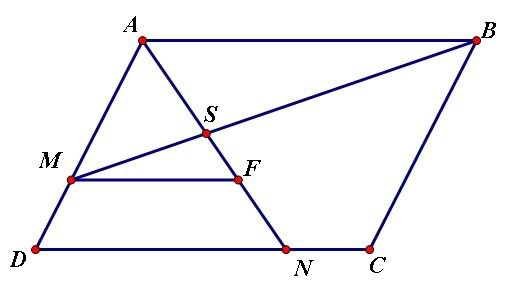
Trên AN lấy F sao cho MF//DC.
Ta có:
$\dfrac{MF}{DN}=\dfrac{MA}{DA}=\dfrac{2}{3}$
$\Rightarrow MF=\dfrac{2}{3}DN=\dfrac{2}{3}.\dfrac{3}{4}DC=\dfrac{1}{2}DC=\dfrac{1}{2}AB$
$\Rightarrow \dfrac{1}{2}=\dfrac{MF}{AB}=\dfrac{SF}{SA}$
$\Rightarrow \dfrac{AS}{AF}=\dfrac{2}{3}$
$\Rightarrow \dfrac{AS}{AN}=\dfrac{AS}{AF}.\dfrac{AF}{AN}=\dfrac{2}{3}.\dfrac{2}{3}=\dfrac{4}{9}$
$\Rightarrow \dfrac{AS}{SN}=\dfrac{4}{5}$

Bài 2:
C1: Theo cách của truclamyentu
$\begin{array}{l}4\sqrt 3 S = \sqrt {3(a + b + c)(a + b - c)(a + c - b)(b + c - a)} \le \sqrt {3(a + b + c)abc} \\\\\le \sqrt {{{(ab + bc + ca)}^2}} = ab + bc + ca \le {a^2} + {b^2} + {c^2}\end{array}$
Xảy ra đẳng thức tại a = b = c tam giác ABC đều.

C2:
Theo hệ quả Bất đẳng thức Bunhiacopski, ta có:
$\dfrac{1}{3}{(a + b + c)^2} \le {a^2} + {b^2} + {c^2}$ (1)
Áp dụng Bất đẳng thức Cauchy, ta có:
$\sqrt {p{{\left[ {\dfrac{{(p - a) + (p - b) + (p - c)}}{3}} \right]}^3}} \ge \sqrt {p(p - a)(p - b)(p - c)} $
$\dfrac{{{p^2}}}{{3\sqrt 3 }} \ge S$ (công thức Hê-rông)
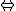$\dfrac{1}{3}.\dfrac{{{{(a + b + c)}^2}}}{{4\sqrt 3 }} \ge S$
Áp dụng (1)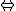 $S \le \dfrac{{{a^2} + {b^2} + {c^2}}}{{4\sqrt 3 }}$
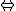$4\sqrt 3 S \le {a^2} + {b^2} + {c^2}$
Xảy ra đẳng thức tại a = b = c tam giác ABC đều.

Không phải đâu bạn, sau một thời gian nhất định thì khoảng cách giữa 2 người sẽ gần lại và ong sẽ bay càng ngày càng ít đi, mình chỉ tự hỏi là khi bắt đầu ong xuất phát từ đâu theo hướng nào nhỉ?