thanhthaiagu
Thống kê
- Nhóm: Thành viên
- Bài viết: 13
- Lượt xem: 3336
- Danh hiệu: Binh nhì
- Tuổi: 39 tuổi
- Ngày sinh: Tháng mười 20, 1984
-
Giới tính
 Bí mật
Bí mật
-
Đến từ
Kiên giang
-
Sở thích
thể thao du lịch
0
Trung bình
Công cụ người dùng
Bạn bè
thanhthaiagu Chưa có ai trong danh sách bạn bè.
Lần ghé thăm cuối
Trong chủ đề: Cực trị của hàm số
29-08-2010 - 09:49
Tôi đề xuất vấn đề này chỉ để đưa ra 1 trường hợp sử dụng quy tắc 2 để tìm tham số m hàm số đạt cực trị tại điểm x=xo, làm sót nghiệm của bài toán. Như vậy trong quá trình giảng dạy hay làm dạng toán này ta nên dùng quy tắc 1 hay là dùng quy tắc 2. Một số bài toán dùng quy tắc 1 tỏ ra khá phức tạp, trong khi dùng quy tắc 2 lại rất dễ dàng. Câu hỏi đặt ra là khi trình bày lời giải bằng cách dùng điều kiện cần và điều kiện đủ như cách của quy tắc 2 có tổng quát cho mọi bài toán hay không. Và khi giải đề thi tốt nghiệp nếu có câu này thì trình bày theo cách nào để đạt điểm tối đa.
Trong chủ đề: Cực trị của hàm số
23-08-2010 - 18:30
Xét bài toán tương tự, nhưng tìm m để hàm số $ y = x^{4}+mx^{2}$ đạt cực tiểu tại điểm x = 0.
Lời giải:
Đạo hàm $y'=4x^{3}+2mx$, mọi x thuộc R
+ Điều kiện cần: Hàm số đạt cực tiểu tại x = 0 là $f'(0)=0$. Điều này đúng với mọi m
+ Điều kiện đủ, đạo hàm cấp 2: $f''(x)=12x^{2}+2m$;
Để hàm số đạt cực tiểu tại điểm x = 0 thì $f''(0)=2m>0$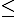 m > 0.
m > 0.
Nếu cho lời giải tương tự ta được: Hàm số đạt cực tiểu tại điểm x = 0 khi và chỉ khi m >0.
Bạn hãy xét với m = 0. Hàm số trở thành $y = x^{4}$ Lúc đó $y'=4x^{3}$. Ta có y'<0 với x<0 và y'>0 với x>0. (Lập bảng xét dấu). Nên hàm số đạt cực tiểu tại điểm x = 0. Giải theo cách trên thì còn thiếu trường hợp m = 0
Lời giải:
Đạo hàm $y'=4x^{3}+2mx$, mọi x thuộc R
+ Điều kiện cần: Hàm số đạt cực tiểu tại x = 0 là $f'(0)=0$. Điều này đúng với mọi m
+ Điều kiện đủ, đạo hàm cấp 2: $f''(x)=12x^{2}+2m$;
Để hàm số đạt cực tiểu tại điểm x = 0 thì $f''(0)=2m>0$
Nếu cho lời giải tương tự ta được: Hàm số đạt cực tiểu tại điểm x = 0 khi và chỉ khi m >0.
Bạn hãy xét với m = 0. Hàm số trở thành $y = x^{4}$ Lúc đó $y'=4x^{3}$. Ta có y'<0 với x<0 và y'>0 với x>0. (Lập bảng xét dấu). Nên hàm số đạt cực tiểu tại điểm x = 0. Giải theo cách trên thì còn thiếu trường hợp m = 0
Trong chủ đề: Gõ công thức toán học lên diễn đàn bằng Mathtype
14-08-2010 - 22:48
$y = x^3 + 2x^2 - \dfrac{1}{6}x + \sqrt 2 x$
Trong chủ đề: Download giả lập FX500MS + FX570MS
10-04-2008 - 08:48
Phần mềm này hỗ trợ đắc lực cho những ai muốn dạy học máy tính Casio
Cám ơn rất nhiều
Cám ơn rất nhiều
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Bài viết: thanhthaiagu


 Tìm kiếm
Tìm kiếm


