Dieu Ha
Thống kê
- Nhóm: Thành viên
- Bài viết: 30
- Lượt xem: 1957
- Danh hiệu: Binh nhất
- Tuổi: 26 tuổi
- Ngày sinh: Tháng mười 10, 1997
-
Giới tính
 Bí mật
Bí mật
-
Đến từ
Somewhere I belong ^^
-
Sở thích
Nghe nhạc, đọc sách, và làm toán, keke ^^
-
Website URL
 http://
http://
Công cụ người dùng
Lần ghé thăm cuối
Trong chủ đề: Một vài bài toán giải phương trình!
02-09-2011 - 08:27
Đề có chút sai sót, mng thông cảm
Đề hoàn chỉnh đây ạ:
g) $\sqrt {x - 1} + x - 3 = \sqrt {4{\rm{x}}^2 - 10{\rm{x}} + 16} $
Trong chủ đề: Một vài bài toán giải phương trình!
31-08-2011 - 20:42
Trong chủ đề: CM 2 góc bằng nhau
03-08-2011 - 21:23
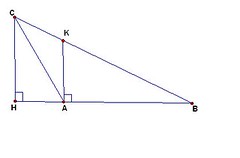
Vẽ $AK \bot AB(K \in BC)$
$ = > \widehat{K{\rm{A}}H} = 90^0 $
$= > \widehat{K{\rm{A}}C} + \widehat{CAH} = 90^0 $
Mà $\widehat{ACB} - \widehat{B} = 90^0 = > \widehat{K{\rm{A}}C} + \widehat{K{\rm{A}}B} - \widehat{B} = 90^0 = > \widehat{K{\rm{A}}C} + 90^0 - \widehat{B} = 90^0 = > \widehat{K{\rm{A}}C} = \widehat{B}$
Mặt khác $\widehat{K{\rm{A}}C} + \widehat{CAH} = \widehat{K{\rm{AH}}}{\rm{ = 90}}^0 = > \widehat{B} + \widehat{CAH} = 90^0$
Mà $\widehat{B} + \widehat{BCH} = 90^0 = > \widehat{CAH} = \widehat{BCH}$ (đpcm)
Ps: Hình hơi nhỏ, bạn thông cảm
Trong chủ đề: Giải phương trình khó!
02-08-2011 - 19:09
$x \ge 1$
Trường hợp $x=2$ là lời giải.
Nếu $1 \le x < 2$ thì $\sqrt[3]{{x+6}}+\sqrt{x-1}> x^{2}-1$
Nếu $x>2$ thì $\sqrt[3]{{x+6}}+\sqrt{x-1}< x^{2}-1$
Giải thích rõ hơn các bất đẳng thức xảy ra trong bài đc ko?, em chưa rõ.
Cảm ơn vì đã giúp đỡ!
Trong chủ đề: Một bài toán khó!
02-08-2011 - 19:02
Đề bài : Cho a,b,c thỏa mãn:
$\dfrac{b^2 + c^2 - a^2 }{2bc} + \dfrac{c^2 + a^2 - b^2 }{2ac} + \dfrac{a^2 + b^2 - c^2 }{2ab} = 1$
Giải :
$\dfrac{b^2 + c^2 - a^2 }{2bc} + \dfrac{c^2 + a^2 - b^2 }{2ac} + \dfrac{a^2 + b^2 - c^2 }{2ab} = 1$
$ \Leftrightarrow (\dfrac{c^2 + a^2 - b^2 }{2ac} - 1) + (\dfrac{a^2 + b^2 - c^2 }{2ab} - 1) + (\dfrac{b^2 + c^2 - a^2 }{2bc} + 1) = 0$
$ \Leftrightarrow \dfrac{c^2 + a^2 - b^2 - 2ac }{2ac} + \dfrac{a^2 + b^2 - c^2 - 2ab}{2ab} + \dfrac{b^2 + c^2 - a^2 + 2bc}{2bc} = 0$
$\Leftrightarrow \dfrac{( a - c )^2 - b^2}{2ac} + \dfrac{( a - b )^2 - c^2}{2ab} + \dfrac{( b + c )^2 - a^2}{2bc} = 0$
$\Rightarrow \dfrac{(a - c - b)(a - c + b)}{2ac}+\dfrac{( a - b - c )(a - b + c)}{2ab} + \dfrac{( b + c - a )( b + c + a )}{2bc } = 0$
$\Leftrightarrow \dfrac{a - b - c}{2}[\dfrac{a - c + b }{ac} + \dfrac{a - b + c}{ab} - \dfrac{a + b + c}{bc}] = 0$
$\Rightarrow (a - b - c)(\dfrac{ab - bc + b^2}{abc} + \dfrac{ac - bc + c^2 }{abc} - \dfrac{a^2 + ab + ac}{abc}) = 0$
$\Leftrightarrow \dfrac{( a - b - c )(ab - bc + b^2 + ac - bc + c^2 - a^2 - ab - ac)}{abc} = 0$
$\Leftrightarrow \dfrac{(a - b - c)(b^2 - 2bc + c^2 - a^2 )}{abc} = 0$
$ \Rightarrow (a - b - c)[( b - c)^2 - a^2] = 0 \Leftrightarrow (a - b - c )( b - c -a )( b - c + a ) = 0$
$ \Rightarrow \left[\begin{array}{l} a = b + c\\a = b - c\\ a = c - b\end{array}\right.$
Với mỗi giá trị a như vậy, thay vào từng biểu thức trên. Ta sẽ có điều phải chứng minh.
P/S: Ai có cách ngắn hơn thì đóng góp nhé !
Thks bạn nhiều nhé!
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Bài viết: Dieu Ha


 Tìm kiếm
Tìm kiếm








