Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 4 tháng 4 và kèm theo đó là bài toán mới:
Bài 36: Cho tam giác $ABC$ có điểm $Lemoine$ là $L$. Lấy $D,E,F$ lần lượt thuộc đoạn $LA,LB,LC$ sao cho $\angle FAC=\angle DCA$ và $\angle EAB=\angle DBA$
Chứng minh rằng: $\angle EBC=\angle FCB$.
Lời giải bài toán gốc của em.
Ta cần có bổ đề sau.
Bổ đề $1$. Cho tam giác $ABC$ có $AB<AC.D$ là trung điểm $BC$. Trung trực $BC$ cắt $AC$ tại $F$. Lấy $E$ thuộc $DF. BE,CE$ lần lượt cắt $AC,AB$ tại $M,N$. Trên $MN$ lấy $T$ sao cho $D(CTEA)=-1$. Khi đó: $D(CT,MN)=-1$
Chứng minh. Gọi $S$ là giao điểm của $AE$ và $MN$. Theo tính chất quen thuộc của hàng điểm điều hòa thì $D(CSEA)=-1\Rightarrow S\equiv T$.
Mặt khác lại có $D(CS,MN)=-1$ nên $D(CT,MN)=-1.\blacksquare$

Hình vẽ bổ đề
Hệ quả.
- Gọi $P$ là trung điểm $AB$. Khi đó $P(AC,DE)=-1$
- $CE,PD$, tiếp tuyến tại $B$ đồng quy.

Hình vẽ
Quay lại giải bài toán tuần $4$ tháng $4$.
Gọi $N$ là trung điểm $AC$. Tương tự ta cũng có $DN,BF,$ tiếp tuyến tại $C$ đồng quy.
Gọi $S,T$ lần lượt là giao của $DP,DN$ với tiếp tuyến tại $B,C. X$ là giao của tiếp tuyến tại $B$ và $C$.

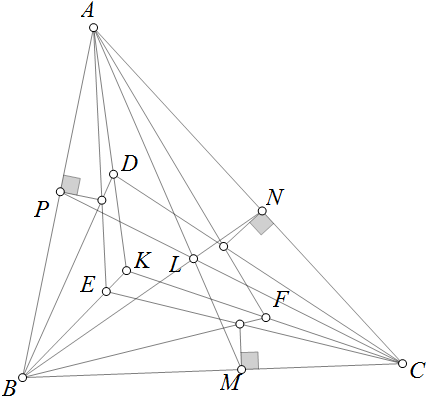
Hình vẽ bài toán
Áp dụng định lí $Menelaus$ cho tam giác $ABX$ với $\overline{D,P,S}$; tam giác $ACX$ với $\overline{D,N,T}$ ta suy ra $\frac {XB}{XS}=\frac {XC}{XT}$
$\Rightarrow BC||ST\Rightarrow \angle TBC=\angle SCB.\blacksquare$
P/s: May mà có sự gợi ý từ thầy Hùng! 
Bài viết đã được chỉnh sửa nội dung bởi baopbc: 25-04-2016 - 13:12