Cám ơn Bảo đã post lại bài mở rộng bài toán miền Tây, sau đây là lời giải dùng hoàn toàn ý tưởng của Bảo được thầy làm chi tiết hơn.
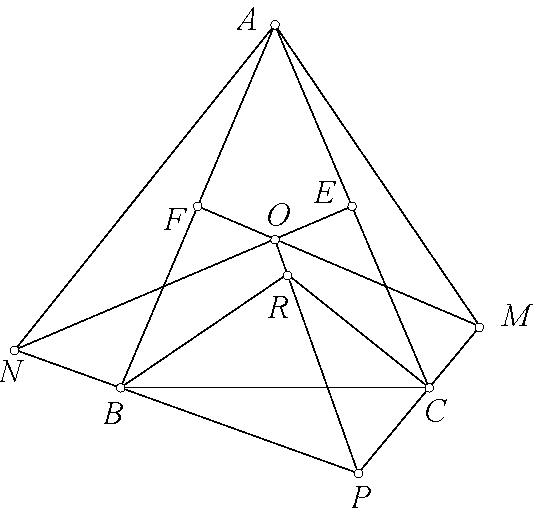
$\boxed{\text{Lời giải bài toán 6.}}$ Ta dễ thấy các đường tròn $(GBE),(GCF)$ đi qua $K$ nên ta viết lại gọn hơn như sau
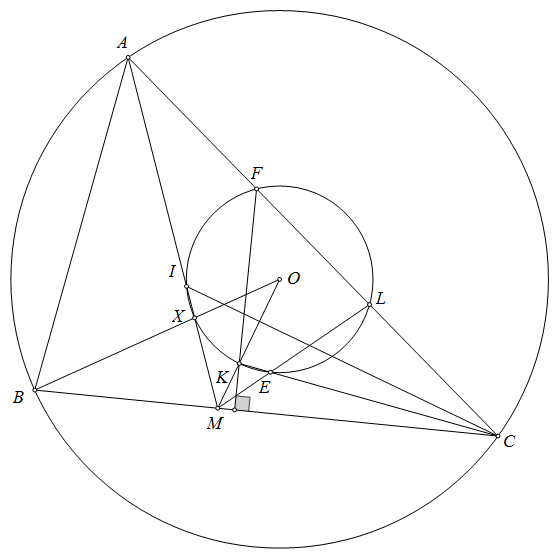
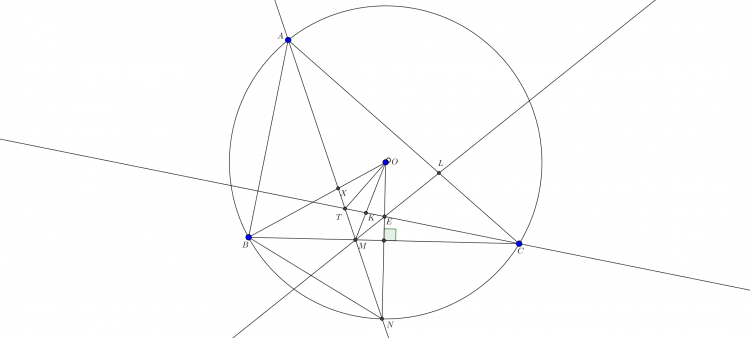
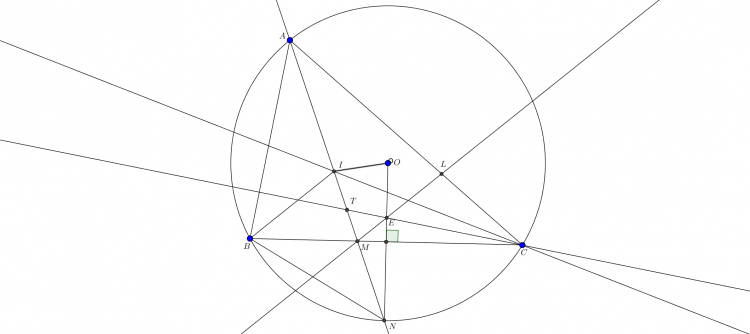
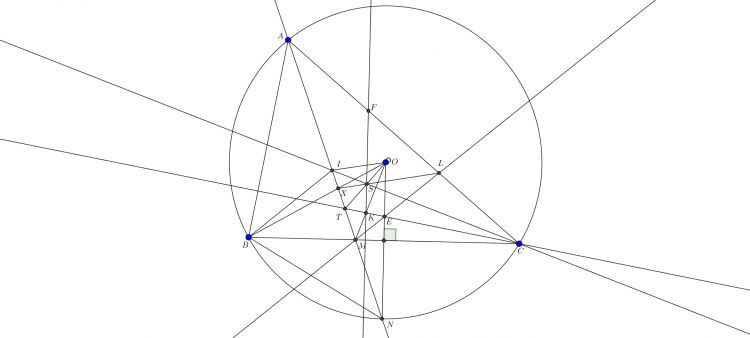
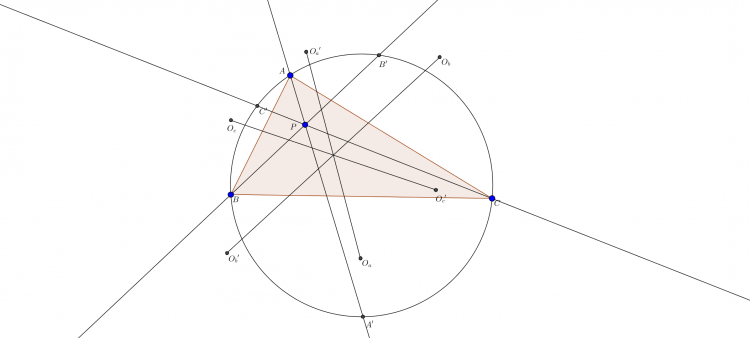
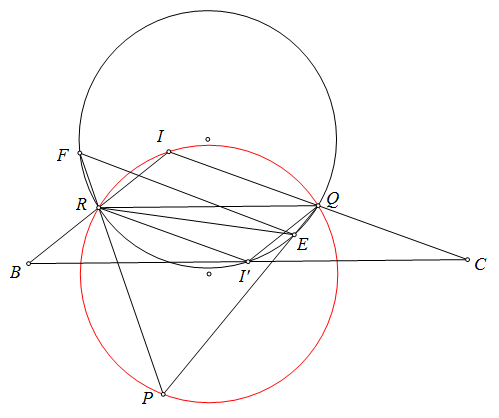
$\boxed{\text{Bài toán 6'.}}$ Cho tam giác $ABC$ có tâm ngoại tiếp $O$. Một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $H$. Gọi $M,N$ là tâm ngoại tiếp các tam giác $KBE,KCF$. $FM$ cắt $EN$ tại $L$. Chứng minh rằng $H,L,O$ thẳng hàng.
Ta dùng các bổ đề sau
Bổ đề 1. Cho tam giác $ABC$ với $E,F$ bất kỳ trên đường thẳng $CA,AB$ thì trực tâm $H$ của tam giác $ABC$ có cũng phương tích với đường tròn đường kính $BE,CF$.
Bổ đề này là kết quả quen thuộc xin không nêu chứng minh.
Bổ đề 2. Cho tứ giác $ABCD$ có $AB$ cắt $CD$ tại $E$. $AD$ cắt $BC$ tại $F$. Thì đường tròn đường kính $AC,BD,EF$ đồng trục.
Chứng minh. Gọi $H,K$ là trực tâm tam giác $ECD,FBC$ theo bổ đề trên dễ thấy $H,K$ có cùng phương tích với các đường tròn đường kính $AC,BD,EF$.
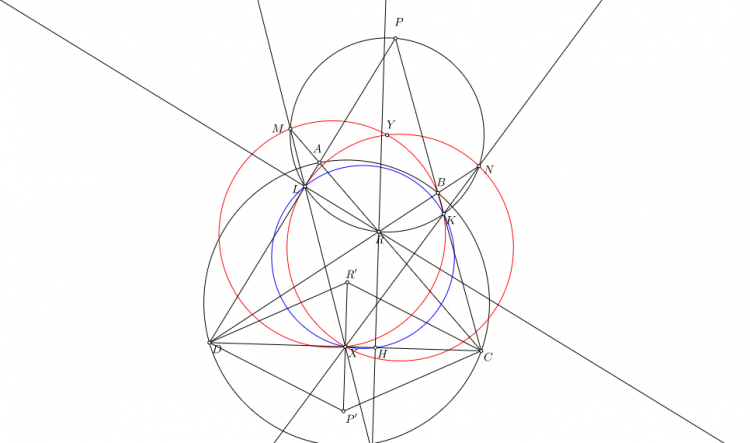
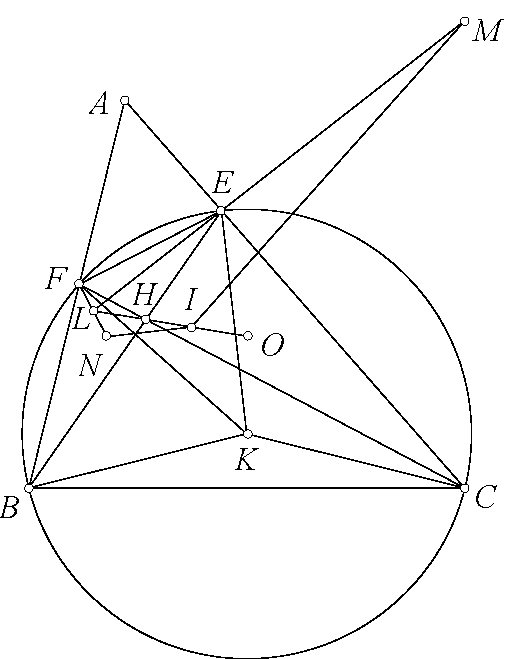
Bổ đề 3. Cho tam giác $ABC$ có $E,F$ thuộc $CA,AB$ sao cho tứ giác $BCEF$ nội tiếp. $P$ là điểm bất kỳ. Lấy $Q$ sao cho $QE\perp AC,QF\perp AB$. $PC,PB$ cắt $QF,QE$ tại $M,N$. Lấy $R$ sao cho $BR\perp AM,CR\perp AN$. Chứng minh rằng $P,Q,R$ thẳng hàng.
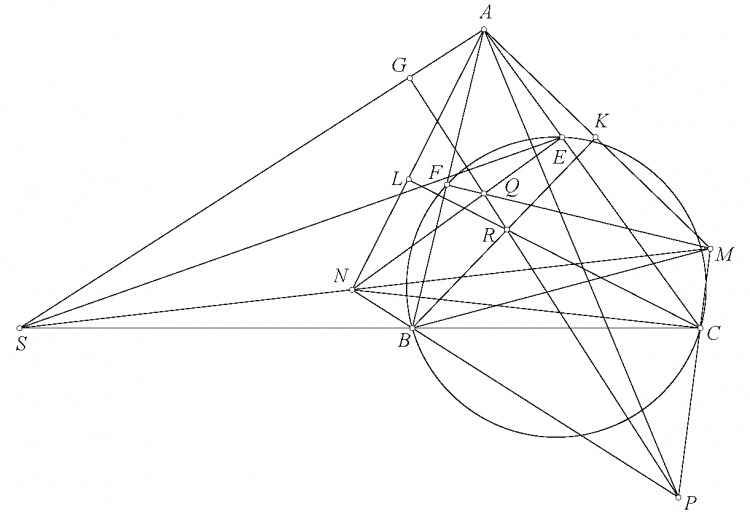
Chứng minh. Gọi $RB,RC$ cắt $AM,AN$ tại $K,L$. $MN$ cắt $BC$ tại $S$. $G$ là hình chiếu của $P$ lên $AS$. Dễ thấy $K,F$ thuộc đường tròn đường kính $BM$ và $L,N$ thuộc đường tròn đường kính $CN$. Nên $AK.AM=AF.AB=AE.AC=AL.AN$. Từ đó dễ thấy $A$ nằm trên trục đẳng phương của các đường tròn đường kính $BM,CN$. Theo bổ đề thì $A$ cũng nằm trên trục đẳng phương chung của các đường tròn đường kính $BM,CN,PS$. Từ đó $AG.AS=AK.AM=AF.AB=AE.AC=AL.AN$. Từ đẳng thức này dễ thấy $G$ nằm trên các đường tròn $(SBF),(SEC)$ suy ra $G$ nằm trên $(AEF)$ là đường tròn đường kính $AQ$ do đó $P,Q,G$ thẳng hàng. Cũng từ đẳng thức thì $G$ nằm trên đường tròn $(ANL),(AMK)$ suy ra $G$ nằm trên $(AKL)$ là đường tròn đường kính $AR$. Từ đó $P,R,G$ thẳng hàng. Như vậy $P,Q,R$ thẳng hàng.
Chú ý bổ đề 3 là của Bảo và chứng minh được tham khảo ở
link.
Hệ quả. Cho tam giác $ABC$ cân tại $A$ với tâm ngoại tiếp $O$. $P$ bất kỳ. $PB,PC$ cắt trung trực $CA,AB$ tại $N,M$. Lấy $R$ sao cho Lấy $R$ sao cho $BR\perp AM,CR\perp AN$. Chứng minh rằng $P,O,R$ thẳng hàng.
Chứng minh. Gọi $E,F$ là trung điểm $CA,AB$ thì tứ giác $BCEF$ nội tiếp. Áp dụng trực tiếp bổ đề 3 trên ta có điều phải chứng minh.
Giải bài toán. Gọi $I$ là tâm, $(KEF)$ theo
kết quả này thì $I$ nằm trên $OH$. Dễ thấy $IM,IN$ là trung trực của $KF,KE$. Đến đây áp dụng hệ quả vào tam giác $KEF$ suy ra $L,H,I$ thẳng hàng. Từ đó $HL$ đi qua $O$.
Nhận xét. Bài toán này là cách viết khác của bài toán nằm trong chuỗi mở rộng bài toán miền tây Trung Quốc năm 2014 sau đây
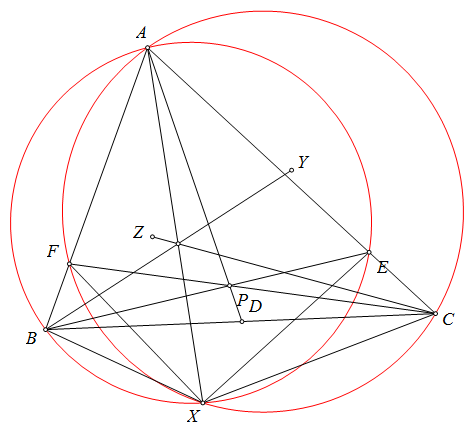
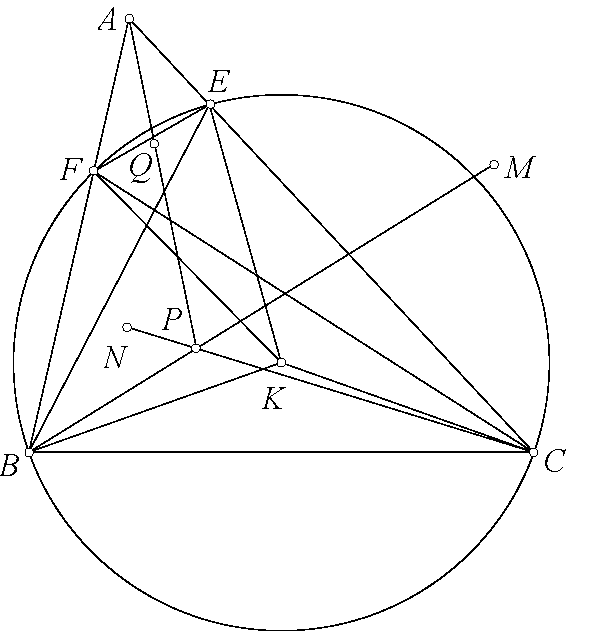
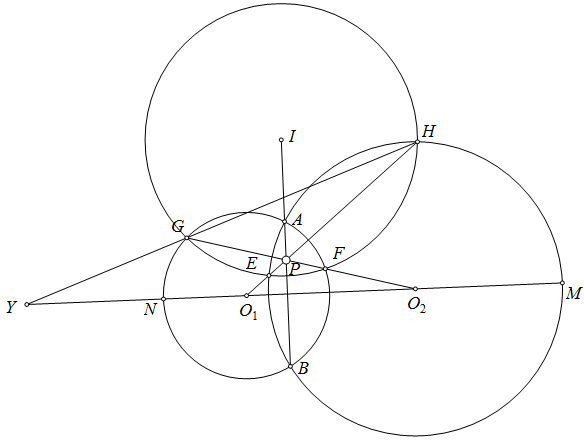
Bài toán. Cho tam giác $ABC$ có tâm ngoại tiếp $O$. Một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $H$. Gọi $M,N$ là tâm ngoại tiếp các tam giác $KCE,KBF$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $AP$ đi qua tâm $(HEF)$.
Bài toán này có thể xem tại
đây.
Toàn bộ lời giải trên là của Nguyến Đức Bảo trong đó bổ đề 3 là quan trọng nhất, lời giải nghịch đảo trong link được tác giả viết lại không nghịch đảo đơn giản hơn nhưng ý tưởng vẫn vậy. Hệ quả có cách chứng minh trực tiếp ngắn hơn.
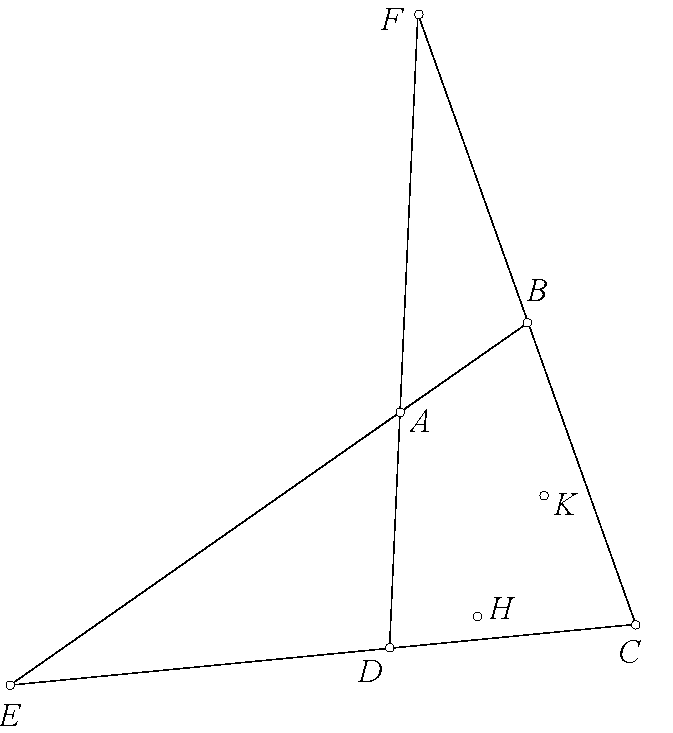
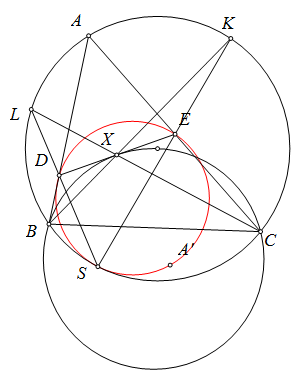
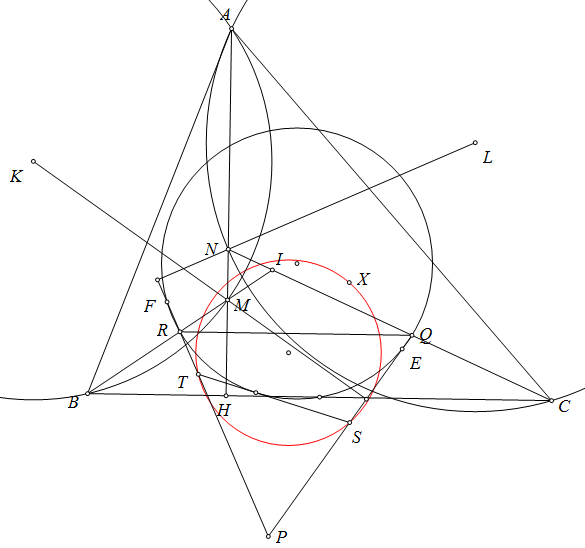
$\boxed{\text{Bài toán 7.}}$ Cho tam giác $ABC$ có đường cao $AH$ và tâm nội tiếp $I$. $IB,IC$ cắt $AH$ tại $M,N$. $K,L$ là tâm ngoại tiếp tam giác $MAB,NAC$. $R,Q$ là trung điểm $IB,IC$. Lấy $P$ sao cho $PR\perp NL,PQ\perp MK$. Một tiếp tuyến thay đổi của đường tròn Euler của tam giác $IBC$ cắt $PQ,PR$ tại $S,T$. $X$ đối xứng $P$ qua $S,T$. Chứng minh rằng đường tròn $(XST)$ luôn tiếp xúc một đường tròn cố định khi tiếp tuyến thay đổi.
Nguồn. Sáng tác + Serbia năm 2016
Xin phép cho mình không tham gia ghi điểm, vì thời gian mình không có nhiều để thường xuyên giải. Có thể coi mình là phương án trợ giúp trong các tình huống khó xử lý của topic này. Mình ủng hộ nhiệt tình và rất vui vì topic này ra đời quy tụ nhiều lời giải và bài toán hình học Olympic hay.
Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:14
Ghi thêm nguồn vì đã có lời giải!
![]()
![]()