Chủ đề này có 434 trả lời

[quanghung86]

Lời giải của Khoa đúng rồi. Được Dương đồng ý, mình đề nghị một bài mới, bài này mình phát triển từ một bài toán Khoa post trên facebook

 

$\boxed{\text{Bài toán 53.}}$ Cho tam giác $ABC$ và $P$ nằm trên đường tròn đường kính $BC$. $PB,PC$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng tâm đường tròn pedal của $P$ ứng với $ABC$ nằm trên đường nối trung điểm $BE,CF$.

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 30-06-2016 - 11:10

[QuangDuong12011998]

Bài thầy vừa đề nghị là trường hợp đặc biệt của bài 52 ạ, khi mà $(PB,PC)=(PE,PF)=\dfrac{\pi}{2}$.

Em đề nghị bài tiếp theo

$\boxed{\text{Bài toán 54}}$(đặc biệt hóa) Cho $\triangle ABC$. Dựng ra ngoài và vào trong hai hình vuông cạnh $BC$. $A_1$, $A_2$ là tâm hai hình vuông thì $A_1A'_1$, $A_2A'_2$ đi qua trực tâm $\triangle ABC$. Trong đó $P'$ là đẳng giác của $P$ với $\triangle ABC$.

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 30-06-2016 - 10:59

[dogsteven]

$\boxed{\text{Bài toán 53.}}$ Với bài toán này, ta có $\widehat{EPF}+\widehat{BPC}=180^o$ nên có thể áp dụng bài toán trước để suy ra điều phải chứng minh.

Ngoài ra còn có một cách giải khác, sử dụng đến bổ đề ERIQ.

Vẫn tiếp tục ý tưởng cũ, gọi $X, Y, Z, T$ là hình chiếu của $P$ trên $FE, EC, CB, BF$, $O$ là tâm $(XYZT)$, $Q$ đối xứng với $P$ qua $O$, $U, V, W$ là hình chiếu của $Q$ trên $FE, EC,CB$

Chứng minh tương tự lời giải trên ta suy ra $U, V, W\in (XYZT)$ và $P, Q$ tạm gọi là đẳng giác trong tứ giác $ABCD$

Ta có $\widehat{EUV}=\widehat{EYX}=\widehat{EPX}=\widehat{EFP}$ nên $UV || FC$, tương tự ta có $VW || EB$ nên $UW$ là đường kính của $(XYZT)$ hay $O$ là trung điểm $UV$

Ta có $\widehat{CQW}=\widehat{CVW}=\widehat{CEP}=\widehat{QEU}$ nên $\Delta CQW \sim \Delta QEU$, do đó $\dfrac{CW}{WQ}=\dfrac{QU}{UE}$

Tương tự ta có $\dfrac{BW}{WQ}=\dfrac{QU}{UF}$, từ đó suy ra $\dfrac{CW}{BW}=\dfrac{UF}{UE}$

Áp dụng bổ đề ERIQ cho ta điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:44

[quanghung86]

Lâu mình không tham giải, thực sự là phát hiện của Dương ở bài 54 khá thú vị. Nhân một bài Bảo vừa hỏi, mình thấy bài này có ý tưởng khá giống nên giải thử theo cách phương tích.

 

Sửa lại ký hiệu như sau cho tiện.

 

Cho tam giác $ABC$ trực tâm $H$. Dựng vào trong tam giác $PBC$ vuông cân tại $P$. Gọi $Q$ đẳng giác $P$ trong tam giác $ABC$. Chứng minh rằng $PQ$ đi qua $H$.

 

 

Lời giải. Do $Q$ đẳng giác $P$ nên gọi $E,F$ là hình chiếu của $Q$ lên $CA,AB$ dễ thấy tam giác $QFB$ và $QEC$ vuông cân. Vậy trong tam giác $QBC$ các tam giác $QFB$ và $QEC$ vuông cân dựng ra ngoài và tam giác $PBC$ vuông cân dựng vào trong nên $EPQF$ là hình bình hành từ đó dễ thấy $P$ là trực tâm tam giác $AEF$. Như vậy dễ thấy $P,H$ đều nằm trên trục đp của đường tròn đường kính $BE,CF$. Gọi $K,L$ là hình chiếu của $C,B$ lên $QF,QE$. Dễ thấy hai tam giác vuông $QCK$ và $QBL$ đồng dạng nên $QK/QL=QC/QB=QE/QF$ hay $QF.QK=QE.QL$. Từ đó $Q$ cũng thuộc trục đp của đường tròn đường kính $BE,CF$.

 

Bài toán này có phát biểu khá gần kiểu hình lớp 7, không rõ có cách nào THCS không ?

 

$\boxed{\text{Bài toán 55.}}$. Cho tam giác $ABC$ nhọn nội tiếp trong đường tròn $(O)$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$. $P$ nằm trong tam giác sao cho $TP=TA$. $PA,PB,PC$ lần lượt cắt $(O)$ tại $D,E,F$ khác $A,B,C$. Dựng tam giác cân $BAQ$ đồng dạng cùng hướng với $FOD$ và tam giác cân $CAR$ đồng dạng cùng hướng với $EOD$. Chứng minh rằng tâm ngoại tiếp tam giác $PQR$ nằm trên $AO$.

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 30-06-2016 - 21:00
Thêm dữ kiện đề bài

[QuangDuong12011998]

Em cũng không biết là bài 54 có cách chứng minh như vậy.

Tổng quát hơn là tính chất 6 đường thẳng đồng quy trên đường thẳng Euler mà em đã post tại http://artofproblems...1202141p5914760

Trong post đó em có ghi nguồn.

Tam giác vuông cân là trường hợp của bài 54.

Đặc biệt khi cho tam giác đều thì các đường thẳng sẽ song song với đường thẳng Euler; khi tam giác cân có góc ở đáy là $\dfrac{\pi}{6}$ thì điểm đồng quy là tâm đường tròn chín điểm.

[quanghung86]

Cám ơn Dương đã gửi link, thầy có thể tổng kết lại được là bài tổng quát nên phát biểu như sau sẽ đẹp

 

Cho tam giác $ABC$ với trực tâm $H$ và tâm ngoại tiếp $O$. $P$ nằm trên trung trực $BC$ và $Q$ đẳng giác $P$. $PQ$ cắt $OH$ tại $R$. Chứng minh rằng $\frac{\overline{RH}}{\overline{RO}}=2-\frac{BC^2}{PC^2}$.

 

Lời giải trong link của Telv đã rõ ràng, tuy nhiên khi phát biểu như trên liệu có các đi khác ?

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 30-06-2016 - 21:16

[dogsteven]

Em có một bài toán tương tự khác.

Cho tam giác $ABC$ và điểm $P$ nằm trên trung trực $BC$, đường tròn ngoại tiếp tam giác $(PBC)$ cắt $AB, AC$ tại $F, E$. Gọi $Q$ là điểm đẳng giác của $P$ trong tam giác $ABC$. Khi đó $PQ, BE, CF$ đồng quy.

[baopbc]

$\boxed{\text{Lời giải bài toán 55}}$ (Tóm tắt)

$M\equiv CR\cap BQ$. Đế ý $\triangle CAR\sim \triangle EOD,\triangle BAQ\sim \triangle FOD$ dễ suy ra $\angle BMY=\angle BPC\implies B,M,P,C$ đồng viên.

Theo kết quả quen thuộc thì $DE=DF$ từ đó $\triangle CAR\sim \triangle BAQ$

Đế ý $\frac{PB}{PC}=\frac{AB}{AC}\implies \frac{PB}{BQ}=\frac{PC}{PR}\implies \triangle RPC\sim \triangle QPB$

$\implies R,Q,P,M$ đồng viên.

$X\equiv CM\cap AB,Y\equiv BM\cap AC$. Đế ý $\angle ACR=\angle ABQ$ nên $B,X,Y,C$ đồng viên $\implies XY\perp AO$

Đế ý $\angle ABM=\angle ACR=\angle ARC\implies A,R,B,M$ đồng viên $\implies XR.XM=XB.XA\implies X$ thuộc trục đẳng phương của $(O)$ và $(PQR)$.

Tương tự kéo theo $XY$ là trục đẳng phương của $(O)$ và $(PQR)\implies XY\perp OK\implies A,O,K$ thẳng hàng.$\blacksquare$

[baopbc]

Nhân đề xuất bài toán mới, mình/em xin đưa ra một lời giải khác cho bài toán 54.

$\boxed{\text{Lời giải bài toán 54}}$ 

$E\equiv BQ\cap AC,F\equiv CQ\cap AB,X\equiv BH\cap AC,Y\equiv CH\cap AC$. 

Dễ thấy $QH$ là trục đẳng phương của $(BE)(CF)$. Gọi $M,N$ theo thứ tự là hình chiếu của $E,F$ lên $BA,AC$.

Dễ thấy $P\equiv XM\cap YN$. Mặt khác $M,N,X,Y$ đồng viên nên $PM.PX=PN.PY$ do đó $P$ thuộc trục đẳng phương của $(BE)(CF)$ hay $P,H,Q$ thẳng hàng.

$\boxed{\text{Bài toán 56}}$ (Thầy Trần Quang Hùng) Cho tam giác $ABC$ ngoại tiếp đường tròn tâm $I.(I)$ tiếp xúc $BC$ tại $D$. Trung trực $AD$ cắt $ID$ tại $M$. Gọi $E,F$ theo thứ tự là trung điểm $AD,AI$. Chứng minh rằng $OM$ chia đôi $EF$ với $(O)\equiv (ABC)$.

PS.

Kết quả này từng được dùng để giải một bài toán trên AoPS

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 01-07-2016 - 17:34

[viet nam in my heart]

$\boxed{\text{Bài toán 56}}$

Bài này đẹp quá, Bảo dẫn lại Link bài này và bài trên AOPS được không

Ta thấy $(M,MA)$ tiếp xúc với $BC$ nên vẽ $(M,MA)$ cắt $(O)$ tại $P$. $AP$ cắt $BC$ tại $Q$

Gọi $X,Y$ lần lượt là tiếp điểm của $(I)$ trên $AC,AB$. $XY$ cắt $BC$ tại $Z$

Ta có: $QD^2=QP.QA=QB.QC$ mà $(ZDBC)=-1$ nên theo hệ thức $Newton$ suy ra $Q$ là trung điểm của $ZD$

Kẻ đường kính $AA'$. $PA'$ cắt $ID$ tại $S$. Ta có: $PSDQ$ nội tiếp nên $\widehat{QSD}=\widehat{QPD}=\widehat{DME}$ suy ra $QS \parallel ME$

Ta có bổ đề quen thuộc $ZI \perp AD$ nên $ZI \parallel ME$

Mặt khác $Q$ là trung điểm $ZD$ nên $S$ là trung điểm $ID$

Gọi $L$ là trung điểm của $EF$ suy ra $L$ là trung điểm $AS$ suy ra $OL \parallel A'S$ suy ra $OL \perp AP$

Mặt khác $OM \perp AP$ nên $O,L,M$ thẳng hàng

Vậy $OM$ chia đôi $EF$ 

Ai đề nghị giúp em bài toán mới với ạ  

[halloffame]

Mình đề xuất 1 bài:

$\boxed{\text{Bài toán 57}}$ (geometry.ru) Cho hình thang $ABCD$ vuông tại $A,D.M,N$ trung điểm $AC,BD.(ABN),(CDM)$ lần lượt cắt $BC$ tại $Q,R.Z$ là trung điểm $MN.$ Chứng minh $ZQ=ZR.$

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 02-07-2016 - 19:44

[baopbc]

Trâu bò vậy!

$\boxed{\text{Lời giải bài toán 57}}$

Áp dụng công thức đường trung tuyến ta chỉ cần chứng minh:

$MQ^2+NQ^2=MR^2+NR^2 \ (1)$

Theo bổ đề $Carnot$ thì $(1)\iff $

$\cos \angle QRM.MR=\cos \angle NQB.NQ$

$\iff \cos \angle ACD.MR=\cos \angle ABD.NQ$

$\iff sin \angle DAC.MR=\sin \angle ADB.NQ$

$P\equiv AC\cap BD$. Theo định lí $Sin$ thì

$\frac{\sin \angle DAP}{\sin \angle ADP}=\frac{PD}{PA}$

Ta cần chỉ ra

$\frac{NQ}{MR}=\frac{PD}{PA} \ (*)$

Tiếp tục sử dụng định lí $Sin$ và công thức diện tích ta suy ra

$\frac{MR}{MD}=\frac{\sin \angle MCB}{\sin \angle MCD}=\frac{PB.BC}{PD.CD}$

Tương tự thì 

$\frac{NQ}{NA}=\frac{PA.AB}{PC.BC}$

Mặt khác $MD=\frac{1}{2}AC \ , \ NA=\frac{1}{2}BD$ nên dễ suy ra $(*)$ đúng hay đẳng thức được chứng minh $\implies NQ=NR.\blacksquare$

PS.

Anh Quân (halloffame) đăng lời giải được không?

Bài toán đề nghị. $\boxed{\text{Bài toán 58}}$ Cho tam giác $ABC$ nội tiếp $(O).I$ bất kì trên phân giác $\angle A.D,E,F$ lần lượt là hình chiếu của $I$ lên $BC,CA,AB.OI$ cắt $BC$ tại $K.L$ thuộc $AK$ sao cho $AI\parallel DL.LD$ cắt $EF$ tại $X$. Chứng minh rằng $X$ là trung điểm $DL$

Kết quả này mình từng mở rộng từ một bài tập của thầy mình, nếu có trùng lặp mong mọi người thông cảm! Bài toán gốc là khi $I\equiv $ tâm nội tiếp của tam giác $ABC$.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:46

[viet nam in my heart]

$\boxed{\text{Lời giải bài toán gốc của bài toán 58}}$

Trước hết ta nhắc lại tính chất sau: Cho tam giác $ABC$ ngoại tiếp $(I)$ với các tiếp điểm trên $BC,CA,AB$ là $D,E,F$. Gọi $A_1,B_1,C_1$ lần lượt là trung điểm $3$ đường cao kẻ từ $A,B,C$ của tam giác $ABC$. Gọi $A_2,B_2,C_2$ lần lượt là chân đường cao kẻ từ $D,E,F$ của tam giác $D,E,F$. Gọi $(O)$ là đường tròn ngoại tiếp tam giác $ABC$. Khi đó $7$ đường thẳng $AA_2,BB_2,CC_2,DA_1,EB_1,FC_1,OI$ đồng quy tại 1 điểm 

Trở lại bài toán:

Gọi $X$ là hình chiếu của $D$ lên $EF$. Kẻ đường cao $AH$ và gọi $S$ là trung điểm của $AH$. $AD$ cắt $OI$ tại $Z$ 

Theo tính chất trên thì $AX,DS,OI$ đồng quy tại điểm $T$ 

Ta có: $D(AHSI)=-1$ nên $(KZTI)=-1 \Leftrightarrow A(KZTI)=-1 \Leftrightarrow  A(KDTI)=-1 $

Lại có $AI$ song song với $DL$ nên theo tính chất của chùm điều hòa ta có điều phải chứng minh 

Lời giải gượng ép quá. Nếu chuyển lời giải này qua bài tổng quát của Bảo tuy tính chất đồng quy vẫn đúng nhưng chứng minh chắc cũng không ngắn, dễ    

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 02-07-2016 - 19:07

[quanghung86]

Nguồn gốc của bài toán 57 là bài số 14 trong này http://geometry.ru/o...13/zaochn-e.pdf

 

Đáp án ở đây http://geometry.ru/o...13/zaochsol.pdf

 

Bài này là bài toán hay có nhiều phát triển và ứng dụng.

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 02-07-2016 - 19:41
Thêm đáp án!

[quanghung86]

Bài của Bảo là mở rộng định lý 1 trong bài viết này http://forumgeom.fau...e4/FG200411.pdf

 

Đây là mở rộng hay, mình biết 1 vài mở rộng nữa trên AoPS, tuy nhiên chúng ta vẫn hãy tập trung giải bài Bảo đề nghị!

[Ngockhanh99k48]

$\boxed{\text{Lời giải bài toán 58}}$

Ta sẽ chứng minh $D$ đối xứng với $L$ qua đường thẳng $EF$. 

Trước hết gọi $L$ đối xứng $D$ qua $EF$ ta sẽ đi chứng minh $AL, OI, BC$ đồng quy. Gọi $K = AL \cap BC$ ta sẽ chứng minh $O, I, K$ thẳng hàng.

$AI$ cắt đường tròn $(O)$ tại điểm thứ hai $N$. Gọi $M, Y, Z$ là hình chiếu của $N$ trên $BC, AB, AC$. $U = AD \cap OM$. $DL$ cắt $OA$ tại $S$. $DI$ cắt $EF$ và $OA$ tại $Z, T$. 

Ta có, theo đường thẳng Simson thì $Y, M, Z$ thẳng hàng. Từ đó qua phép vị tự tâm $A$ ta có $A, Z, M$ thẳng hàng. Dễ thấy $\triangle OAN$ và $\triangle ZLD$ là hai tam giác cân và $\widehat{ONA}=\widehat{ZDL}$ nên $ZL \parallel OA$. Suy ra $\frac{\overline{DZ}}{\overline{DT}}=\frac{\overline{DL}}{\overline{DS}}$. Hay là $\frac{\overline{UM}}{\overline{UO}}=\frac{\overline{DL}}{\overline{DS}}$. Suy ra $D(OKAI)=D(OMUI)=\frac{\overline{UO}}{\overline{UM}}=\frac{\overline{DS}}{\overline{DL}}=A(SLDI)=A(OKDI)$. Từ đó $O, I, K$ thẳng hàng và ta có đpcm.

P/S: Thầy (hoặc bạn nào đó) ra giúp em (mình) bài mới được không ạ?

 

[lucifer97]

Đề nghị bài mới.

$\boxed{\text{Bài toán 59}}$ ( Sáng tác) Cho $ABC$ nội tiếp $(O)$ có $AD$ là đường kính. $BD$ giao $AC$ tại $M, CD$ giao $AB$ tại $N, AD$ giao $BC$ ở $P.$ Trung tuyến xuất phát từ $P$ của tam giác $MNP$ cắt $(O)$ tại $I. I$ đối xứng $K$ qua $MN,$ Chứng minh $(KMN)$ tiếp xúc $(O)$

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:47

[halloffame]

Mình đề xuất 1 bài:
 

$\boxed{\text{Bài toán 60.}}$ (Mathematical Reflections) Cho tam giác $ABC$ nội tiếp $(O),$ đường tròn $A-inmixtilinear$ là $(I_a)$ tiếp xúc trong $(O)$ tại $A_1.$ $A_2$ đối xứng $A_1$ qua $I_a.$ Tương tự có $B_2,C_2.$ Chứng minh $AA_2,BB_2,CC_2$ đồng quy.

@quanghung86: Chúng ta hạn chế đề xuất 2 bài nhưng hai bài này đều hay vậy hãy để cả 2 bài mọi người cùng thảo luận.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:47

[viet nam in my heart]

$\boxed{\text{Lời giải bài toán 59}}$

Tranh thủ trước giờ trận Pháp Iceland 

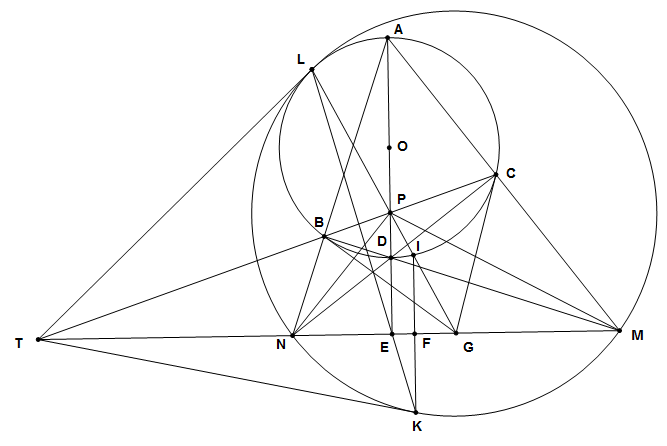
Dễ thấy $D$ là trực tâm của tam giác $AMN$.

Kẻ đường cao $AE$ của tam giác $AMN$

Gọi $F$ là hình chiếu của $I$ trên $MN$. Gọi $G$ là trung điểm của $MN$

Giả sử $GP$ cắt $(O)$ tại điểm thứ hai là $L$. Gọi $T$ là giao điểm của $BC$ và $MN$

Ta có: $(TPBC)$=-1 nên $T,P$ liên hợp đối với $(O)$ 

Do $G$ là trung điểm của $MN$ và $NC,MB$ là hai đường cao của tam giác $AMN$ nên theo một bổ đề quen thuộc thì $GB,GC$ là tiếp tuyến của $(O)$

Từ đó $BC$ là đường đối cực của $G$ đối với $(O)$. Mà $T \in BC$ nên $G$ nằm trên đường đối cực của $T$ đối với $(O)$

Suy ra $IL$ là đường đối cực của $T$ đối với $(O)$. Suy ra $TI,TL$ là tiếp tuyến của $(O$)

Từ đó $TK^2=TI^2=TB.TC$ nên $TK$ là tiếp tuyến của $(MNK)$ hay $K$ thuộc đường đối cực của $T$ đối với $(MNK)$

Mặt khác $(TENM)=-1$ nên $E$ cũng thuộc đường đối cực của $T$ đối với $(MNK)$

Do đó $KE$ là đường đối cực của $T$ đối với $(MNK)$

Ta sẽ chứng minh $K,E,L$ thẳng hàng, theo định lý Thales cần chứng minh $\dfrac{LP}{LI}=\dfrac{PE}{KI}=\dfrac{PE}{2IF}=\dfrac{GP}{2GI}$ (đúng vì $(GPIL)=-1$)

Do đó $KL$ là đối cực của $T$ đối với $(MNK)$ mà $TL=TI=TK$ nên $TL$ cũng là tiếp tuyến của $(MNK)$ 

Do $TL$ là tiếp tuyến chung của $(MNK)$ và $(O)$ nên $(MNK)$ tiếp xúc với $(O)$ $\blacksquare$

 

Vài năm trước trên báo THTT thầy Hùng cũng từng đăng một bài có một cấu hình tương tự. Nên mình đề xuất luôn bài đó làm bài 61

 

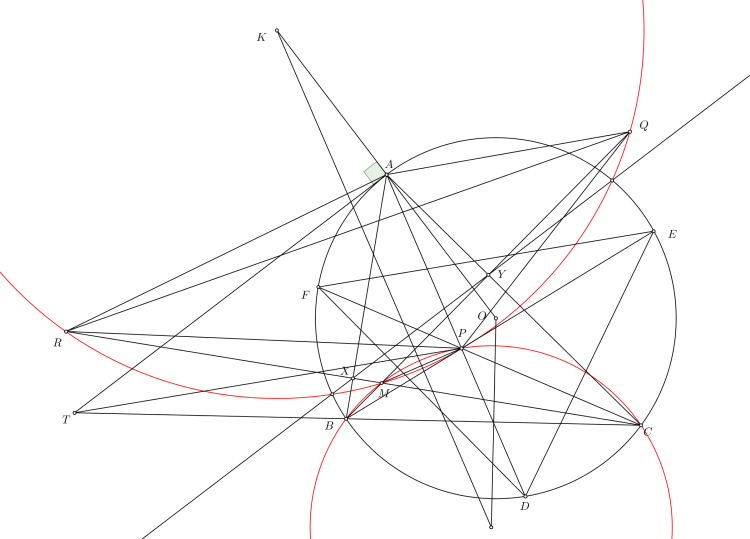
$\boxed{\text{Bài toán 61.}}$ Cho tam giác $ABC$ nội tiếp $(O)$ với các đường cao $BE,CF$. $AD$ là đường kính của $(O)$. $DB,DC$ cắt $AC,AB$ lần lượt tại $M,N$. $P,Q$ thuộc $E,F$ sao cho $PB,QC$ vuông góc với $BC$. Đường thẳng qua $A$ vuông góc với $QN,PM$ cắt $(O)$ tại $X,Y$. Tiếp tuyến của $(O)$ tại $X,Y$ cắt nhau tại $J$. Chứng minh răng $JD \perp BC.$ 

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:48
Sửa lại đề một chút cho đẹp hơn!

[halloffame]

$\boxed{\text{Lời giải bài toán 61}}$

Trước hết, ta chứng minh $QN$ đi qua trung điểm $A_1$ của $BC.$ Gọi $QC$ cắt $AB$ tại $Z.$

Áp dụng định lý Menelaus cho tam giác $BCZ$ với các điểm $Q,A_1,N$ và tam giác $CAZ$ với các điểm $F,E,Q$ ta được: 

$Q,A_1,N$ thẳng hàng $\Leftrightarrow$ $\frac{CQ}{QZ}=\frac{NB}{NZ}$ 

$\Leftrightarrow \frac{NB}{NZ}.\frac{FZ}{FA}.\frac{AE}{EC}=1. \Leftrightarrow \frac{AB}{FA} . \frac{FZ}{NZ} =1 \Leftrightarrow \frac{FB}{FA} = \frac{NF}{FZ} (1).$

Áp dụng hệ thức lượng trong các tam giác vuông $ACN,ZCB$ ta thấy (1) đúng. Vậy tương tự ta suy ra $QN,PM,BC$ đồng quy ở $A_1.$

Theo định lý về đường thẳng Gauss của tứ giác toàn phần thì $OA_1$ đi qua trung điểm $A_2$ của $MN.$

Đường thẳng qua $A$ song song $BC$ cắt lại $(O)$ ở $J_1$ , theo tính chất của tứ giác điều hòa thì ta thấy yêu cầu của đề bài tương đương với việc chứng minh $(AJ_1,AD,AY,AX) =-1.$ (2)

Vẽ tia $A_{1}x$ song song với $MN.$

Chú ý $A_{1}x,A_{1}A_2,MA_1,NA_1$ lần lượt vuông góc $AD,AJ_1,AY,AX$ và $A_2$ trung điểm $MN,$ đồng thời $A_{1}x \parallel MN,$ ta thấy (2) đúng. Ta có điều phải chứng minh.

Mình sẽ đề nghị bài mới sau khi bài 60 có lời giải.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:49
Thêm hình