Ngày thi 3
Bài 1: Cho dãy ($a_{n}$) thỏa mãn $a_0=1$ và $a_{n+1}=\frac{-3}{7}(\sqrt{(a_n^2+1)^3}+a_n^3)$
CMR: $(a_n)$ hội tụ và tìm $lim(a_n)$
Bài 2: Tìm tất cả n nguyên dương sao cho $3^n+4^n+5^n\mid 60^n$
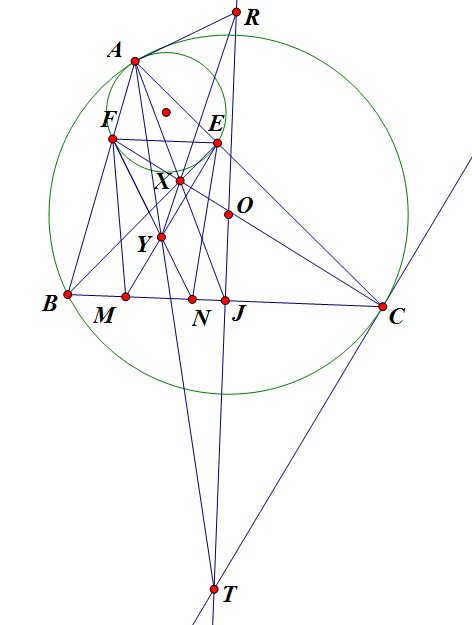
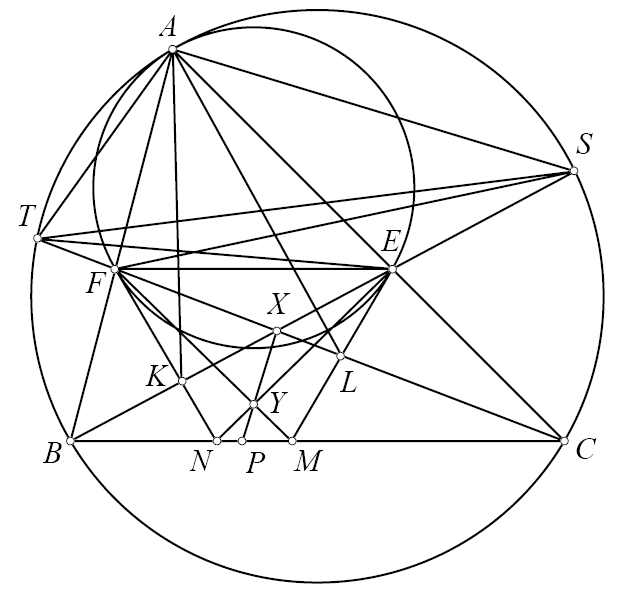
Bài 3: Cho $\Delta ABC$, $E,F$ lần lượt thuộc $CA,AB$ sao cho $EF\parallel BC$. Tiếp tuyến tại $E,F$ của $(AEF)$ cắt $BC$ tại $M,N$ $BE,CF$ lần lượt cắt $FN,EM$ tại $K,L$.
(a) CMR: $\widehat{KAB}=\widehat{LAC}$
(b) $BE$ cắt $CF$ tại $X$, $EN$ cắt $FM$ tại $Y$. CMR: $XY$ đi qua điểm cố định khi $E,F$ di chuyển.
Bài 4: $x,y,z$ là 3 số nguyên dương sao cho $x+y+z=1$ Tìm giá trị lớn nhất của
$P=\sqrt{\frac{x^2y}{4x+5y}}+\sqrt{\frac{y^2z}{4y+5z}}+\sqrt{\frac{z^2x}{4z+5x}}$
Ngày thi 4
Bài 1: Tìm tất cả các hàm $f:\mathbb{R}\rightarrow \mathbb{R}$ thỏa mãn $f(x-1)f(y^2)=y(xy)-yf(y)$
Bài 2: Cho dãy số $(a_n)$ thỏa mãn $\left\{\begin{matrix} a_0=a_1=5\\ a_{n+1}=7a_n-a_{n-1}+44 \end{matrix}\right.$
CMR: $a_n$ là tổng 2 số chính phương
Bài 3: Cho $\Delta ABC$, đường tròn $(K)$ đi qua $B,C$ cắt đoạn $AC,AB$ tại $E,F$. $M,N$ đối xứng $B,C$ lần lượt qua $E,F$. Tiếp tuyến tại $A$ của $(AMN)$ cắt $MN,BC$ tại $P,Q$. Chứng minh rằng $A$ là trung điểm của $PQ$
Bài 4: Cho bảng $n\times n$ $(n\in N^*)$ và số $k\leqslant n$ Điền vào các ô trong bảng $n\times n$ các số thực thuộc đoạn $[-1;1]$ sao cho tổng các số trên mỗi bảng con $k\times k$ bằng $0$. Tìm giá trị lớn nhất của tổng tất cả các số trên bảng $n\times n$