ĐỀ THI OLYMPIC CHUYÊN KHOA HỌC TỰ NHIÊN 2016
Ngày 1 (07/05/2016)
Câu 1. Giải hệ phương trình $$\begin{cases}x + y + xy = 3 \\ y^{3} + 13y = 6x^{2} + 8\end{cases}$$
Câu 2. Tìm tất cả các bộ số nguyên dương $(x, y, z)$ thỏa mãn phương trình $$7^{x} + 3^{y} = 2^{z}$$
Câu 3. Cho tam giác $ABC$ nhọn có tâm nội tiếp $I$. Đường thẳng qua $I$ vuông góc với $AI$ cắt cạnh $CA, AB$ lần lượt tại $M, N$. Gọi $E$ đối xứng $C$ qua $M$, $F$ đối xứng $B$ qua $N$. Giả sử $E, F$ đều lần lượt thuộc các đoạn thẳng $CA, AB$. Gọi $(K), (L)$ lần lượt là đường tròn ngoại tiếp các tam giác $ICE, IBF$.
- Chứng minh rằng $(K)$ và $(L)$ tiếp xúc nhau tại $I$.
- Gọi $EF$ theo thứ tự cắt $(K), (L)$ tại $P, Q$ khác $E, F$. Chứng minh rằng $EP = FQ$.
Câu 4. Cho dãy số $(a_{n})_{n\in\mathbb{Z}^{+}}$ xác định như sau $$\begin{cases}a_{1} = 0 \\ a_{2} = 1 \\ a_{2n} = 2a_{n} + 1 \\ a_{2n + 1} = 2a_{n}\end{cases}$$ với mọi $n \in \mathbb{Z}^{+}$. Chứng minh rằng tồn tại vô số số nguyên dương $k$ sao cho $a_{k} = 2016$ và tìm số nguyên dương $k$ nhỏ nhất thỏa mãn điều này.
Ngày 2 (08/05/2016)
Câu 5. Hỏi có tồn tại hay không các số nguyên dương $a, b, c$ thỏa mãn $2a \ge 5c \ge 4b$ sao cho tồn tại số nguyên dương $n \ge 3$ và đa thức hệ số nguyên $P_{n}(x) = a_{0}x^{n} + a_{1}x^{n - 1} + \cdots + a_{n - 3}x^{3} + ax^{2} - bx + c$ có $n$ nghiệm phân biệt.
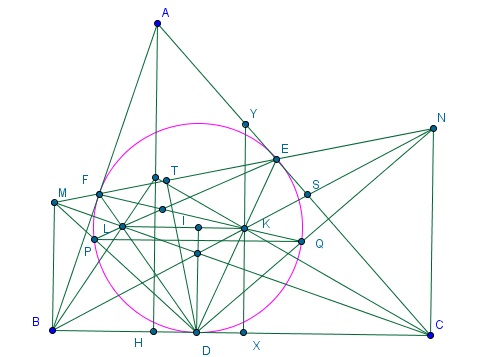
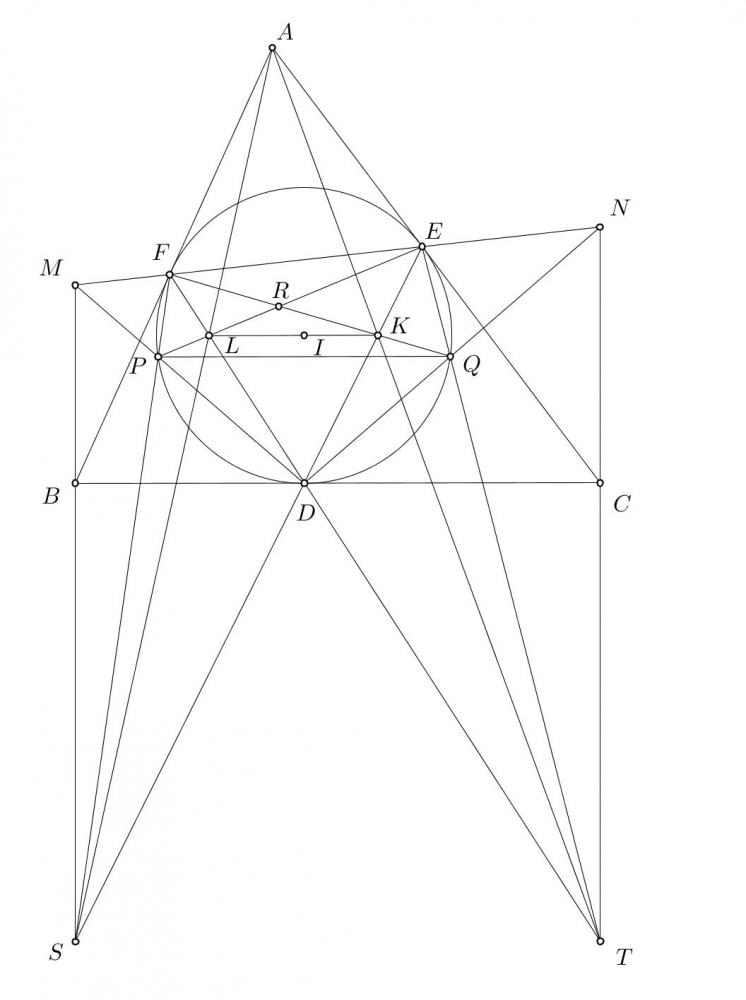
Câu 6. Cho tam giác $ABC$, đường tròn nội tiếp $(I)$ tiếp xúc với $BC, CA, AB$ tại $D, E, F$. Các điểm $M, N$ thuộc đường thẳng $EF$ sao cho $BM, CN$ vuông góc với $BC$. Và $DM, DN$ lần lượt cắt $(I)$ tại $P, Q$.
- Chứng minh rằng $PQ // BC$
- Gọi $K, L$ lần lượt là giao điểm của $DE$ và $QF$, $DF$ và $PE$. Chứng minh rằng $KL // BC$.
- Chứng minh rằng $I, K, L$ thẳng hàng
Câu 7. Cho $a, b, c$ là các số thực dương thỏa mãn $ab + bc + ca + 2abc = 1$. Chứng minh rằng $$\sum\frac{a(a + 1)}{(2a + 1)^{2}}\le \frac{9}{16}$$
Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 08-05-2016 - 17:23