hôm nay tạch luôn câu phương trình, quên ko ghi vào giấy thi

đề thi tuyển sinh vào 10 chuyên lam sơn thanh hóa môn toán(vòng 1)
#1
 Đã gửi 05-06-2016 - 11:17
Đã gửi 05-06-2016 - 11:17

#2
 Đã gửi 05-06-2016 - 11:30
Đã gửi 05-06-2016 - 11:30

hôm nay tạch luôn câu phương trình, quên ko ghi vào giấy thi
Mình xin giải câu 3b nhé:
Giải phương trình: $x^2+4x-7=(x+4)\sqrt{x^2-7}(1)$.
Đk: $x^2\ge 7$
$(1)\iff x^2+4x-7-4(x+4)=(x+4)[\sqrt{x^2-7}-4]$
$\iff (x^2-23)[\sqrt{x^2-7}+4]=(x+4)(x^2-23)$
$\iff x^2=23(n),\sqrt{x^2-7}+4=x+4(2)$
Đến đây bạn tự giải tiếp nhé
Bài viết đã được chỉnh sửa nội dung bởi TanSan26: 05-06-2016 - 11:30
- trambau, qnhipy001 và Ho Hoai An thích
A vẩu
#3
 Đã gửi 05-06-2016 - 11:31
Đã gửi 05-06-2016 - 11:31

Mình xin giải câu 3b nhé:
Giải phương trình: $x^2+4x-7=(x+4)\sqrt{x^2-7}(1)$.
Đk: $x^2\ge 7$
$(1)\iff x^2+4x-7-4(x+4)=(x+4)[\sqrt{x^2-7}-4]$
$\iff (x^2-23)[\sqrt{x^2-7}+4]=(x+4)(x^2-23)$
$\iff x^2=23(n),\sqrt{x^2-7}+4=x+4(2)$
Đến đây bạn tự giải tiếp nhé
cần câu c bài hình kia, câu đó mình làm rồi nhưng ko ghi vào giấy
#4
 Đã gửi 05-06-2016 - 11:34
Đã gửi 05-06-2016 - 11:34

Câu 5 :
Ta có:$P=\sum \frac{x(yz+1)^2}{z^2(xz+1)}$
$=\sum \frac{\dfrac{\left ( yz+1 \right )^2}{z^2}}{\dfrac{(xz+1)}{x}}$
$=\sum \frac{\left ( y+\dfrac{1}{z} \right )^2}{z+\dfrac{1}{x}}$
$\geq \frac{\left ( x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )^2}{x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}}$
$=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq x+y+z+\frac{9}{x+y+z}$
$=\left ( x+y+z+\frac{9}{4(x+y+z)} \right )+\frac{27}{4(x+y+z)}$
$\geq 2\sqrt{\frac{9}{4}}+\frac{27}{4.\dfrac{3}{2}}=\frac{15}{2}$
- nntien, I Love MC, tpdtthltvp và 8 người khác yêu thích
#5
 Đã gửi 05-06-2016 - 11:36
Đã gửi 05-06-2016 - 11:36

Câu 5 :
Ta có:$P=\sum \frac{x(yz+1)^2}{z^2(xz+1)}$
$=\sum \frac{\dfrac{\left ( yz+1 \right )^2}{z^2}}{\dfrac{(xz+1)}{x}}$
$=\sum \frac{\left ( y+\dfrac{1}{z} \right )^2}{z+\dfrac{1}{x}}$
$\geq \frac{\left ( x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )^2}{x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}}$
$=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq x+y+z+\frac{9}{x+y+z}$
$=\left ( x+y+z+\frac{9}{4(x+y+z)} \right )+\frac{27}{4(x+y+z)}$
$\geq 2\sqrt{\frac{9}{4}}+\frac{27}{4.\dfrac{3}{2}}=\frac{15}{2}$
câu đó e cx full luôn rồi, còn câu hình kinh niên nữa, anh làm ơn giúp e với
#6
 Đã gửi 05-06-2016 - 11:49
Đã gửi 05-06-2016 - 11:49

Mình giải câu 5 như sau:
Từ giả thiết suy ra $xyz\le \frac{1}{8}$.
Khi đó áp dụng $AM-GM$ ta có:
$P\ge 3\sqrt[3]{\frac{\prod(xy+1)}{xyz}}$.
Đến đây ta tìm min của $\frac{\prod(xy+1)}{xyz}(=Q)$
Ta có: $Q=abc+\frac{1}{abc}+(a+b+c)+(\sum \frac{1}{a})\ge (abc+\frac{1}{abc})+[(a+b+c)+\frac{9}{a+b+c}]$
$\iff Q\ge (abc+\frac{1}{64abc})+(a+b+c+\frac{9}{4(a+b+c)})+\frac{63}{64abc}+\frac{27}{4(a+b+c)}$.
Đến đây kết hợp $AM-GM$ và đk ban đầu $=> Q\ge \frac{125}{8}=> P\ge \frac{15}{2}$.
Vậy $Min P=\frac{15}{2}$. Dấu $=$ xảy ra khi $x=y=z=\frac{1}{2}$
Bài viết đã được chỉnh sửa nội dung bởi TanSan26: 05-06-2016 - 11:52
A vẩu
#7
 Đã gửi 05-06-2016 - 11:49
Đã gửi 05-06-2016 - 11:49

Mình giải câu 5 như sau:
Từ giả thiết suy ra $xyz\le \frac{1}{8}$.
Khi đó áp dụng $AM-GM$ ta có:
$P\ge \sqrt[3]{\frac{\prod(xy+1)}{xyz}}$.
Đến đây ta tìm min của $\frac{\prod(xy+1)}{xyz}(=Q)$
Ta có: $Q=abc+\frac{1}{abc}+(a+b+c)+(\sum \frac{1}{a})\ge (abc+\frac{1}{abc})+[(a+b+c)+\frac{9}{a+b+c}]$
$\iff Q\ge (abc+\frac{1}{64abc})+(a+b+c+\frac{9}{4(a+b+c)})\frac{63}{64abc}+\frac{27}{4(a+b+c)}$.
Đến đây kết hợp $AM-GM$ và đk ban đầu $=> Q\ge \frac{125}{8}=> P\ge \frac{15}{2}$.
Vậy $Min P=\frac{15}{2}$. Dấu $=$ xảy ra khi $x=y=z=\frac{1}{2}$
mình chưa học mấy cái kí hiệu đó đâu ![]()
#8
 Đã gửi 05-06-2016 - 12:28
Đã gửi 05-06-2016 - 12:28

Câu 4:
a. tứ giác DCBO nội tiếp => góc ODC = góc OBM
b. Ta có CO là phân giác góc NCM và CO vuông góc MN => CO là đường trung trực của MN (1) => CM=CN.
Mà AB//CN, theo Talet => DC=BA=BM, mà OD=OB => $\triangle OBM = \triangle ODC$ (c-g-c)
=> OC=OM. Mà theo (1) => OM=ON => OM=ON=OC (đpcm)
c. Ta có $KB.KD=IB^2-IK^2$ (xem như một bài toán nhỏ)
Từ đó yêu cầu bài toán tương đương: $\frac{ND}{MB}=\frac{KB}{KD}$
Vì CK là phân giác của tam giác CBD => $\frac{KB}{KD}=\frac{CB}{CD}$, mà $ND=AD=CB$ và $MB=AB=CD$
=> đpcm.
Chứng minh bài toán nhỏ: qua K kẻ đường thẳng vuông góc với IK cắt (O) tại E, F => KE=KF
Tam giác KDE đồng dạng tam giác KBF=> $KB.KD=KE.KF=KE^2=IE^2-IK^2=IB^2-IK^2$.
Bài viết đã được chỉnh sửa nội dung bởi nntien: 05-06-2016 - 12:31
- O0NgocDuy0O, ThoiPhong, Hannie và 3 người khác yêu thích
$Maths$, $Smart Home$ and $Penjing$
123 Phạm Thị Ngư
#9
 Đã gửi 05-06-2016 - 12:35
Đã gửi 05-06-2016 - 12:35

Câu 3 b.
Bình phương hai vế thành phương trình bậc 4, sau đó sử dụng máy CASIO đoán nghiệm => tách nhân tử.
Nếu biết làm bằng cách này thì 100% thí sinh đều làm được!
Các bạn thi CASIO đều vọc qua câu dạng này!
- trambau yêu thích
$Maths$, $Smart Home$ and $Penjing$
123 Phạm Thị Ngư
#10
 Đã gửi 05-06-2016 - 12:39
Đã gửi 05-06-2016 - 12:39

c) (Mượn hình ở trên)
Gọi G, H là giao điểm của IK với đường tròn tâm I => $\\IB^{2} - IK^{2} = (IB-IK).(IB+IK) = (IG - IK).(IH+IK)= KG.KH$
Phương tích => $\\KG.KH = KD.KB$
=> VP = $\ \frac{KB}{KD}$
VT = $\ \frac{ND}{MB} = \frac{AD}{AB} = \frac{CB}{CD}$ (ở câu b chứng minh tam giác ADN và ABM cân)
T/c đường phân giác => $\ \frac{CB}{CD} = \frac{KB}{KD}$ => đpcm
Bài viết đã được chỉnh sửa nội dung bởi cunshockbaby: 05-06-2016 - 12:46
- trambau yêu thích
#13
 Đã gửi 05-06-2016 - 20:56
Đã gửi 05-06-2016 - 20:56

câu 3b pt làm thế này được không nhỉ
ĐK $x^2 \geq 7$
PT ban đầu
<=> $\frac{x^2+4x-7}{x+4}=\sqrt{x^2-7} (x \neq -4)$
Tiếp tục đặt điều kiện
$\frac{x^2+4x-7}{x+4} \geq 0$
Rồi bình phương 2 vế nhân chéo lên giải pt cuối, kiểm tra đk
Mình thấy làm vậy quá dài còn nếu bình phương lên lúc ban đầu thì không ổn lắm. mong các bạn góp ý ![]()
Bài viết đã được chỉnh sửa nội dung bởi Zeref: 05-06-2016 - 20:57
- trambau yêu thích
#14
 Đã gửi 05-06-2016 - 21:08
Đã gửi 05-06-2016 - 21:08

câu 3b pt làm thế này được không nhỉ
ĐK $x^2 \geq 7$
PT ban đầu
<=> $\frac{x^2+4x-7}{x+4}=\sqrt{x^2-7} (x \neq -4)$
Tiếp tục đặt điều kiện
$\frac{x^2+4x-7}{x+4} \geq 0$
Rồi bình phương 2 vế nhân chéo lên giải pt cuối, kiểm tra đk
Mình thấy làm vậy quá dài còn nếu bình phương lên lúc ban đầu thì không ổn lắm. mong các bạn góp ý
Bình phương hai vế, ta được:
$x^4+8 x^3+2 x^2-56 x+49=x^4+8 x^3+9 x^2-56 x-112$
<=>$x=±\sqrt{23}$
Thử lại hai nghiêm đều thỏa mãn.
$Maths$, $Smart Home$ and $Penjing$
123 Phạm Thị Ngư
#17
 Đã gửi 05-06-2016 - 22:38
Đã gửi 05-06-2016 - 22:38

câu 3,b đặt căn x^2-7 =a ==> a^2=x^2-7 thì pt trở thành a^2+4x=(x+4)a
<=>a^2+4x-ax-4a=0 <=>a(a-x)-4(a-x)=0
<=>(a-4)(a-x)=0
<=>a=4 hoặc a=x rồi thay vào là ra
- trambau và xuantungjinkaido thích
#18
 Đã gửi 06-06-2016 - 16:21
Đã gửi 06-06-2016 - 16:21

#19
 Đã gửi 07-06-2016 - 09:46
Đã gửi 07-06-2016 - 09:46

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN
THANH HÓA NĂM HỌC 2016 – 2017
ĐỀ THI CHÍNH THỨC Môn thi: Toán (Chung cho các thí sinh)
Ngày thi: 05/06/2016
Thời gian: 120 phút
Bài 1: Cho biểu thức $A=\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}+1}{\sqrt{x}-3}+\frac{3-11\sqrt{x}}{9-x}$ (Với $x\geq 0;x\neq 9$)
a) Rút gọn A
b) Tìm tất cả các giá trị của x để $A\geq 0$
Bài 2: a) Trong hệ trục tọa độ Oxy cho hai đường thẳng (d1): $y=(m^{2}-1)x+2m$ (m là tham số) và (d2): $y=3x+4$. Tìm các giá trị của tham số m để đường thẳng (d1) và (d2) song song với nhau
b) Cho phương trình:$x^{2}-2(m-1)x+2m-5=0$ (với m là tham số). Tìm các giá trị của m để phương trình đó có hai nghiệm x1; x2 thỏa mãn $(x_{1}^{2}-2mx_{1}+2m-1)(x_{2}-2)\leq 0$
Bài 3: a) Giải hệ phương trình $\left\{\begin{matrix} 2\sqrt{x}+y^{2}=3 & \\ 3\sqrt{x}-2y^{2}=1 & \end{matrix}\right.$
b) Giải phương trinh $x^{2}+4x-7=(x+4)\sqrt{x^{2}-7}$
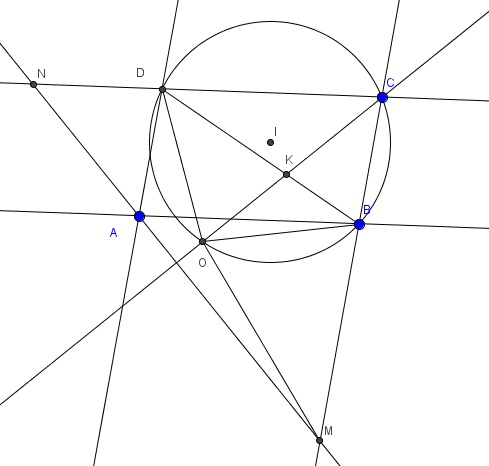
Bài 4: Cho hình bình hành ABCD với $\widehat{BAD}< 90^{0}$, tia phân giác $\widehat{BCD}< 90^{0}$ cắt đường tròn ngoại tiếp tam giác BCD tại O (khác C), kẻ đường thẳng (d) đi qua A và vuông góc với CO. Đường thẳng (d) cắt đường thẳng CB, CD lần lượt tại M và N.
a) Chứng minh rằng $\widehat{OBM}=\widehat{ODC}$
b) Chứng minh ∆OBM = ∆ODC và O là tâm đường tròn ngoại tiếp tam giác CMN
c) Gọi K là giao điểm của OC và BD, I là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng $\frac{ND}{MB}=\frac{IB^{2}-IK^{2}}{KD^{2}}$
Bài 5: Cho ba số thực dương x, y, z thỏa mãn $x+y+z\leq \frac{3}{2}$
Tìm giá trị nhỏ nhất của biểu thức $P=\frac{x(yz+1)^{2}}{z^{2}(zx+1)}+\frac{y(zx+1)^{2}}{x^{2}(xy+1)}+\frac{z(xy+1)^{2}}{y^{2}(yz+1)}$
- linhtrang1602, hoakute và Ho Hoai An thích
#20
 Đã gửi 13-06-2016 - 15:24
Đã gửi 13-06-2016 - 15:24

0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh