ĐẠI HỌC KHOA HỌC TỰ NHIÊN ĐỀ THI TUYỂN SINH VÀO LỚP 10
THPT KHOA HỌC TỰ NHIÊN THPT CHUYÊN NĂM 2015-2016
Môn:Toán (Vòng 2)
Thời gian làm bài 150 phút (Không kể thời gian giao đề)
$\boxed{\textrm{ĐỀ THI CHÍNH THỨC}}$
Câu 1 (3,5 điểm)
1)Giải hệ phương trình:
$$\left\{\begin{matrix} x^2+4y^2=5 & & \\ 4x^2y+8xy^2+5x+10y=1& & \end{matrix}\right.$$
2)Giải phương trình:
$$\sqrt{5x^2+6x+5}=\frac{64x^3+4x}{5x^2+6x+6}$$
Câu 2 (2,5 điểm)
1)Với $x,y$ là những số nguyên thỏa mãn đẳng thức $\frac{x^2-1}{2}=\frac{y^2-1}{3}$.Chứng minh rằng:$x^2-y^2$ chia hết cho $40$
2)Tìm tất cả các cặp số nguyên $(x;y)$ thỏa mãn đẳng thức :
$$x^4+2x^2=y^3$$
Câu 3 (3 điểm)
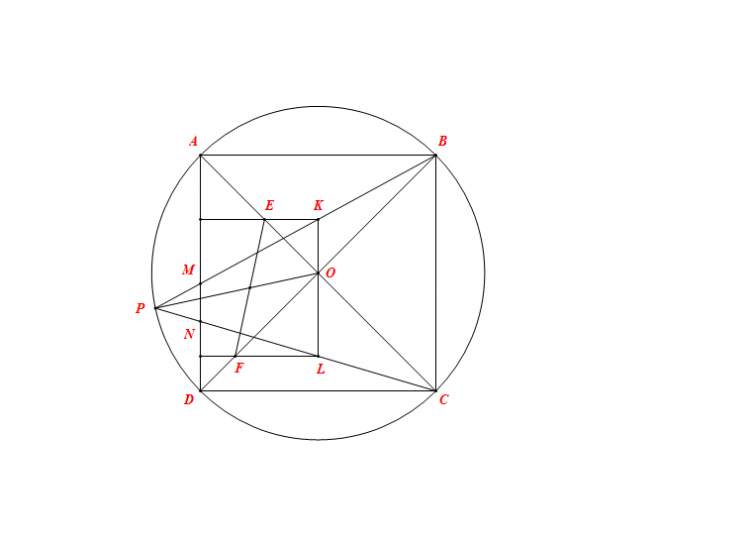
Cho hình vuông $ABCD$ nội tiếp đường tròn tâm $(O)$ . $P$ là điểm thuộc cung nhỏ $AD$ của đường tròn $(O)$ và $P$ khác $A,D$ .Các đường thẳng $PB,PC$ lần lược cắt $AD$ tại $M,N$ . Đường trung trực của $AM$ cắt đường thẳng $AC,PB$ lần lượt tại $E,K$ . Đường trung trực $DN$ cắt các đường thẳng $BD,PC$ lần lượt tại $F,L$
a)Chứng minh ba điểm $K,O,L$ thẳng hàng
b)Chứng minh đường thẳng $PO$ đi qua trung điểm của đọa thẳng $EF$
c)Giả sử đường thẳng $EK$ cắt đường thẳng $BD$ tại $S$, các đường thẳng $FL$ và $AC$ cắt nhau tại $T$,đường thẳng $ST$ cắt các đường thẳng $PB,PC$ lần lượt tại $U$ và $V$ .Chứng minh rằng bốn điểm $K,L,V,U$ cùng thuộc một đường tròn
Câu 4 (1 điểm)
Chứng minh rằng với mọi số tự nhiên $n\geq 3$ luôn tồn tại một cách xếp bộ $n$ số $1,2,3,...,n$ thành $x_1,x_2,...,x_n$ sao cho $x_j\neq \frac{x_i+x_k}{2}$ với mọi bộ chỉ số $(i;j;k)$ mà $1\leq i<j<k\leq n$
Cán bộ coi thi không giải thích gì thêm
Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 05-06-2016 - 12:13