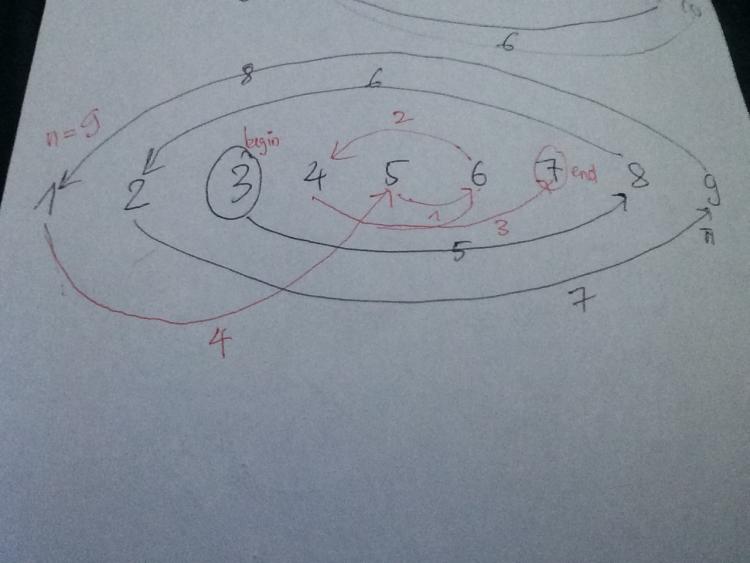
Bài 1. Cho $44$ cái lỗ phân biệt trên một cái rãnh là đường thẳng và $2017$ con kiến. Mỗi con kiến sẽ chui lên từ một cái lỗ và bò đến một cái lỗ khác với vận tốc không đổi rồi chui xuống đó. Gọi $T$ là tập các thời điểm mà con kiến chui lên hoặc chui xuống các cái lỗ. Biết rằng vận tốc của các con kiến đôi một khác nhau và $|T| \le 45.$ Chứng minh rằng tồn tại ít nhất hai con kiến nào đó không gặp nhau.
Bài 2. Với mỗi số nguyên dương $n$, đặt $x_n = C_{2n}^n$.
a) Chứng minh rằng nếu $\dfrac{2017^k}{2} < n < 2017^k$ với $k$ là số nguyên dương nào đó thì $x_n$ là bội của $2017$.
b) Tìm tất cả số nguyên dương $h > 1$ để tồn tại các số nguyên dương $N,T$ sao cho với mọi $n>N$ thì $x_n$ là dãy số tuần hoàn theo modulo $h$ với chu kỳ $T$.
Bài 3. Cho tam giác $ABC$ ngoại tiếp đường tròn $(I)$ và $(I)$ tiếp xúc với các cạnh $BC, CA, AB$
lần lượt tại $D, E, F.$ Gọi $I_b, I_c$ lần lượt là các tâm đường tròn bàng tiếp góc B, C của tam giác $ABC.$ Gọi $P, Q$ lần lượt là trung điểm $I_bE, I_cF.$ Giả sử $(PAC)$ cắt $AB$ tại $R$ và $(QAB)$ cắt $AC$ tại $S.$
a) Chứng minh rằng $PR, QS, AI$ đồng quy.
b) DE, DF lần lượt cắt $I_bI_c$ tại $K, J.$ $EJ$ cắt $FK$ tại $M$ và $PE, QF$ cắt $(PAC),(QAB)$ lần lượt tại $X,Y$. Chứng minh rằng $BY, CX, AM$ đồng quy.
Bài 4. Cho tam giác $ABC$ nội tiếp đường tròn $(O).$ Điểm $A$ di động trên $(O)$ sao cho $AB > BC$ và $M$ là trung điểm $AC.$ Đường tròn đường kính $BM$ cắt $(O)$ tại $R.$ Giả sử $RM$ cắt $(O)$ tại $Q,$ cắt $BC$ tại $P.$ Đường tròn đường kính $BP$ cắt $AB, BO$ lần lượt tại $K, S.$
a) Chứng minh rằng $SR$ đi qua trung điểm $KP.$
b) Gọi $N$ là trung điểm $BC.$ Trục đẳng phương của hai đường tròn đường kính AN, BM cắt SR tại $E.$ Chứng minh rằng $ME$ đi qua một điểm cố định.
Bài 5. Cho $2017$ số thực dương $a_1,a_1,...,a_{2017}.$ Với mỗi $n>2017,$ ta đặt
\[a_n=\max \{a_{i_1}a_{i_2}a_{i_3}|i_1+i_2+i_3=n, 1 \le i_1 \le i_2 \le i_3 \le n-1 \}. \]
Chứng minh rằng tồn tại $m$ nguyên dương không vượt quá $2017$ và $N >4m$ sao cho $a_na_{n-4m}=a_{n-2m}^2$ với mọi $n>N$.
Bài 6. Với mỗi số nguyên dương $n$, xét $a_1,a_2, \ldots, a_{2n}$ là hoán vị của $2n$ số nguyên dương đầu tiên. Một hoán vị như thế được gọi là đẹp nếu với mọi $1 \le i < j \le 2n$ thì $a_i+a_{n+i}=2n+1$ và $a_i-a_{i+1}$ không đồng dư với $a_j-a_{j+1}$ theo modulo $2n+1$. Quy ước $a_{2n+1}=a_1$.
a) Với $n=6$, hãy chỉ ra một hoán vị đẹp.
b) Chứng minh rằng với mỗi $n$ nguyên dương thì luôn tồn tại một hoán vị đẹp.
Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 26-03-2017 - 15:35