Như vậy lời giải cho bài Tuần 3 tháng 5/2017 đã được đưa tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng và bạn Nguyễn Tiến Hoàng. Xin trích dẫn lại hai bài toán:
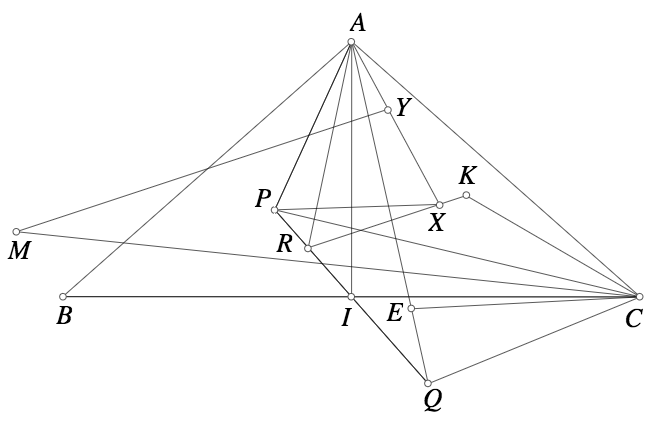
Bài 1. Cho tam giác $ABC$ cân tại $A$. $P,Q$ là hai điểm đối xứng nhau qua trung điểm $BC$ sao cho $PQ \perp AB$. $K$ là lâm ngoại tiếp tam giác $APQ$ và $AR$ là đường đối trung của tam giác $APQ$. $M$ đối xứng $C$ qua phân giác $\angle PAQ$. Lấy $E$ trên $AQ$ sao cho $CE=CQ$. Giả sử có $X$ thuộc $KR$ và $Y$ thuộc $AX$ sao cho $AX=AP, AY=EQ$. Chứng minh rằng $MY \parallel KR$.
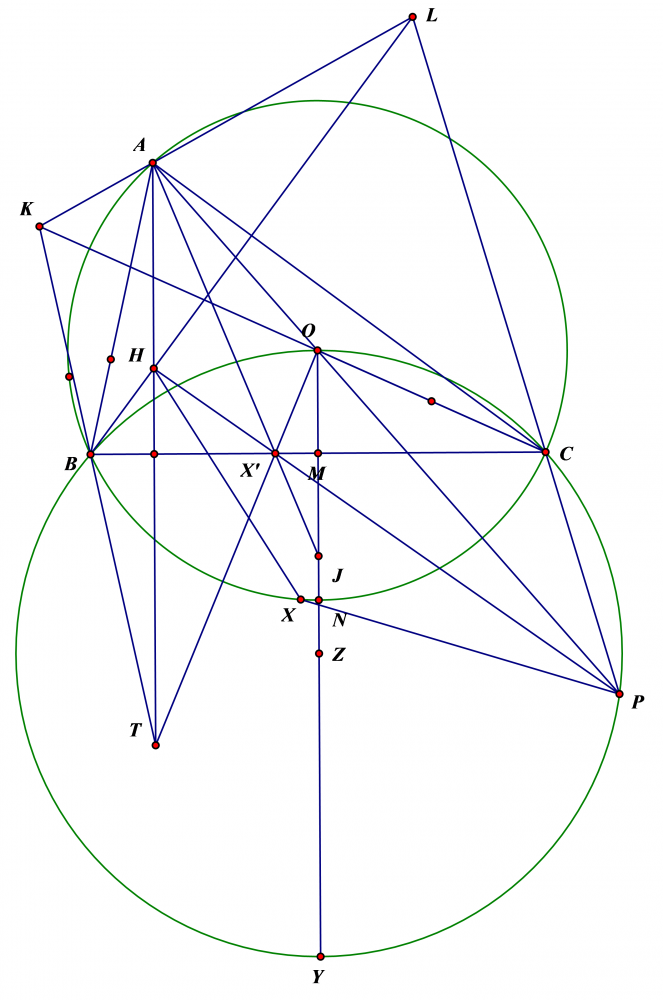
Bài 2. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định với $B,C$ cố định và $A$ di chuyển trên $(O)$. $AO$ cắt đường tròn ngoại tiếp tam giác $BOC$ tại $P$ khác $A$. $H$ là trực tâm tam giác $ABC$. Đường tròn ngoại tiếp tam giác $APH$ cắt $(O)$ tại $X$ khác $A$. Chứng minh rằng $AX$ luôn đi qua điểm cố định.