daovuquang

Bài làm của bạn Tru09 với BlackBot giống nhau 1 cách lạ kì.

Bài làm của daovuquang:

1) Dễ có $\widehat{HBA}=\widehat{HAC}$ ( cùng phụ $\widehat{HAB}$)
$\Rightarrow \widehat{HBI}=\widehat{HAJ}$.
Mà $\widehat{BHI}=\widehat{AHJ}(=45^o)\Rightarrow \triangle{HBI} \sim \triangle{HAJ}$
$\Rightarrow \frac{HI}{HJ}=\frac{BH}{AH}$.
Mà $\triangle{HBA} \sim \triangle{ABC}\Rightarrow \frac{BH}{AH}=\frac{AB}{AC}$
$\Rightarrow \frac{HI}{HJ}=\frac{AB}{AC}$.
Mặt khác, $\widehat{IHJ}=\widehat{IHA}+\widehat{AHJ}=45^o+45^o=90^o=\widehat{BAC}$
$\Rightarrow \triangle{ABC} \sim \triangle{HIK}$
$\Rightarrow$ đpcm.
2) Tia $BI$ cắt $AJ$ tại $D$, tia $CJ$ cắt $AI$ tại $E$.
Dễ chứng minh $B,I,Q,D$ và $C,J,Q,E$ thẳng hàng.
Nhận xét: $\widehat{BAD}=\widehat{BAH}+\widehat{HAD}=\widehat{BCA}+\frac{\widehat{HAC}}{2}=\widehat{BCA}+\frac{\widehat{CBA}}{2}=(\widehat{BCA}+\widehat{CBA})-\frac{\widehat{ABC}}{2}=90^o-\frac{\widehat{ABC}}{2}$
$\Rightarrow \widehat{BAD}+\widehat{ABD}=90^o-\frac{\widehat{ABC}}{2}+\frac{\widehat{ABC}}{2}=90^o$
$\Rightarrow \widehat{ADB}=90^o$
$\Rightarrow IQ \perp AJ$.
Tương tự, $JQ \perp AI$.
Suy ra $Q$ là trực tâm $\triangle{AIJ} \Rightarrow AQ \perp IJ \Rightarrow$ đpcm.
==========
Điểm bài làm: 10
Tổng điểm: 55

Theo em, Box BĐT THCS nên có đủ các bài toán lớp 6, 7, 8, 9.

Vậy mong bạn đóng góp những bài toán lớp 6, 7 cho VMF.

2. Đề bài bạn viết sai. Lời giải ở đây: http://diendantoanho...frac-1cright10/
3. Phải chứng minh: $(a-1)(a-3)(a-4)(a-6)\geq -10$
$\Leftrightarrow (a^2-7a+6)(a^2-7a+12)\geq -10\; (1)$.
Đặt $a^2-7a+9=x$ thì $(1) \Leftrightarrow (x-3)(x+3)\geq -10$
$\Leftrightarrow x^2+1\geq 0$
$\Rightarrow$ luôn đúng.
Dấu bằng không xảy ra.
4. Nhận xét: $\frac{1}{a^2+bc}+\frac{1}{b^2+ca}+\frac{1}{c^2+ab}$
$\leq \frac{1}{2a\sqrt{bc}}+\frac{1}{2b\sqrt{ca}}+\frac{1}{2c\sqrt{ab}}$
$=\frac{\sqrt{bc}+\sqrt{ca}+\sqrt{ab}}{2abc}$
$\leq \frac{a+b+c}{2abc}$.
Dấu bằng xảy ra khi $a=b=c$.
6. Đã có ở đây: http://diendantoanho...right-2leq-9bc/

1. Gọi $a_1;a_2;...;a_n$ là $n$ số thỏa mãn điều kiện trên.
Nếu $n$ lẻ thì $a_1;a_2;...;a_n$ đều lẻ $\Rightarrow$ tổng của chúng cũng lẻ $\Rightarrow$ vô lí.
Nếu $n=4k+2=2(2k+1)$ thì trong $a_1;a_2;...;a_n$ có 1 số chẵn, còn lại toàn lẻ. Giả sử $a_1$ chẵn. Khi đó tổng $a_2+a_3+...+a_n$ chẵn. Tổng trên có số số hạng là số lẻ ($4k+1$), các số toàn lẻ $\Rightarrow a_2+a_3+...+a_n$ lẻ $\Rightarrow$ vô lí.
Vậy $4|n$.
2. Đặt $n=4k$.
Xét $n=2.2k.(-1)^{2n+2}.1^{n-2}.(-1)^{n-2}$ thì $2+2n+(2n+2).(-1)+(n-2).1+(n-2).(-1)=0$.
$n$ số nguyên bao gồm $2;2k;3n$ số $(-1)$ và $n-2$ số $1$ thỏa mãn điều kiện bài cho.

Lời giải khác:
Phương trình bài cho:
$x^4+6x^3+14x^2+20x-4xy-16y+4y^2+20=0$
$\Leftrightarrow (x^4+6x^3+13x^2+12x+4)+(x^2+4y^2-4xy+8x-16y+16)=0$
$\Leftrightarrow [(x^2+3x)^2+4(x^2+3x)+4]+[(x-2y)^2+8(x-2y)+16]=0$
$\Leftrightarrow (x^2+3x+2)^2+(x-2y+4)^2=0\; (1)$.
Nhận thấy $VT(1)\geq VP(1)$ nên dấu bằng phải xảy ra:
$\left\{\begin{matrix}
x^2+3x+2=0\; (2)\\
x-2y+4=0\; (3)
\end{matrix}\right.$
Ta có: $(2)\Leftrightarrow (x+1)(x+2)=0$
$\Leftrightarrow x=-1$ hoặc $x=-2$.
Mặt khác, $(3) \Leftrightarrow y=\frac{x+4}{2}$.
Xét $x=-1$ thì $y=\frac{-1+4}{2}=\frac{3}{2}$. Vì $y$ không là số nguyên $\Rightarrow$ loại.
Xét $x=-2$ thì $y=\frac{-2+4}{2}=1$ (chọn).
Kết luận: Vậy hệ có nghiệm $(x;y)=(-2;1)$.
________________
Điểm thưởng: $d_t=10$

Lần sau đề nghị bạn Bui Nhat Son vẽ hình trước khi nói.

Thực tế thì cái biểu thức bậc 4 kia vẫn có thể phân tích được bằng phương pháp hệ số bất đinh.

Mở rộng 1: Cho $a_1;a_2;...;a_n$ là các số tùy ý thuộc $[0;1]$. Chứng minh rằng:
$$\frac{a_1}{a_2+a_3+...+a_n+1}+\frac{a_2}{a_3+a_4+...+a_1+1}+...+\frac{a_n}{a_1+a_2+...+a_{n-1}+1}+(1-a_1)(1-a_2)...(1-a_n)\leq 1$$

Bổ đề: Bất đẳng thức Cauchy (AM-GM) cho $n$ số. Có thể tham khảo ở đây: http://en.wikipedia....geometric_means

Ta xét 2 trường hợp:
TH1: $a_i$ bất kì ($1\le i \le n;\; i \in \mathbb{N}$) bằng $0$ hoặc $1$, trừ $(a_1;a_2;...;a_n)=(0;0;...;0);(1;1;...;1)$. Khi đó dấu đẳng thức xảy ra.
TH2: $(a_1;a_2;...;a_n)$ khác ở trên:
Giả sử $a_1=max(a_1;a_2;...;a_n)$.
Ta có: $\frac{a_1}{a_2+a_3+...+a_n+1}+\frac{a_2}{a_3+a_4+...+a_1+1}+...+\frac{a_n}{a_1+a_2+...+a_{n-1}+1}\leq \frac{a_1+a_2+...+a_n}{a_2+a_3+...+a_n+1}=1-\frac{1-a_1}{a_2+a_3+...+a_n+1}$.
Phải chứng minh: $1-\frac{1-a_1}{a_2+a_3+...+a_n+1}+(1-a_1)(1-a_2)...(1-a_n)\leq 1$
$\Leftrightarrow (1-a_1)[(1-a_2)(1-a_3)...(1-a_n)-\frac{1}{a_2+a_3+...+a_n+1}] \leq 0$.
Dễ thấy $1-a_1 \geq 0$. Ta sẽ chứng minh $(1-a_2)(1-a_3)...(1-a_n)-\frac{1}{a_2+a_3+...+a_n+1}\leq 0$
$\Leftrightarrow (1-a_2)(1-a_3)...(1-a_n)(a_2+a_3+...+a_n+1)\leq 1$.
Áp dụng bổ đề cho các số dương $1-a_2;1-a_3;...;1-a_n;a_2+a_3+...+a_n+1$:
$(1-a_2)(1-a_3)...(1-a_n)(a_2+a_3+...+a_n+1)\leq (\frac{1-a_2+1-a_3+...+1-a_n+a_2+a_3+...+a_n+1}{n})^n=(\frac{n}{n})^n=1$
$\Rightarrow$ đpcm.
Dấu đẳng thức xảy ra $\Leftrightarrow (a_1;a_2;...;a_n)=(0;0;...;0);(1;1;...;1)$.
Kết luận: Vậy $\frac{a_1}{a_2+a_3+...+a_n+1}+\frac{a_2}{a_3+a_4+...+a_1+1}+...+\frac{a_n}{a_1+a_2+...+a_{n-1}+1}+(1-a_1)(1-a_2)...(1-a_n)\leq 1$.
Dấu đẳng thức xảy ra $\Leftrightarrow a_i$ bất kì ($1\le i \le n;\; i \in \mathbb{N}$) bằng $0$ hoặc $1$.

Bài làm của daovuquang:
Bổ đề: Với $x;y;z\geq 0$, chứng minh rằng: $xyz \leq \frac{(x+y+z)^3}{27}\; (1)$.
Chứng minh: Ta sẽ chứng minh bất đẳng thức phụ sau: $x+y+z \geq 3\sqrt[3]{xyz}\; (2)$.
$(2) \Leftrightarrow x+y+z+\sqrt[3]{xyz}\geq 4\sqrt[3]{xyz}$.
Áp dụng BĐT Cauchy 2 số:
$\left\{\begin{matrix}
a+b \geq 2\sqrt{ab}=2\sqrt[6]{a^3b^3}\\
c+\sqrt[3]{abc}\geq 2\sqrt{c\sqrt[3]{abc}}=2\sqrt[6]{abc^4}\\
2(\sqrt[6]{a^3b^3}+\sqrt[6]{abc^4})\geq 4\sqrt[12]{a^4b^4c^4}=4\sqrt[3]{abc}
\end{matrix}\right.$
$\Rightarrow (2)$ luôn đúng.
Áp dụng vào $(1)$: $\frac{(x+y+z)^3}{27}\geq \frac{(3\sqrt[3]{xyz})^3}{27}=\frac{27xyz}{27}=xyz$.
Dấu đẳng thức xảy ra $\Leftrightarrow x=y=z$.

Trường hợp 1: $(a;b;c)=(1;0;0);(0;1;0);(0;0;1);(1;1;0);(1;0;1);(0;1;1)$ thì đẳng thức xảy ra.
Trường hợp 2: Với $(a;b;c)$ khác trường hợp trên, không giảm tính tổng quát, giả sử $a=max[a;b;c]$.
Khi đó: $\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}\leq \frac{a}{b+c+1}+\frac{b}{b+c+1}+\frac{c}{b+c+1}=\frac{a+b+c}{b+c+1}=1+\frac{a-1}{b+c+1}$
Phải chứng minh: $1+\frac{a-1}{b+c+1}+(1-a)(1-b)(1-c) \leq 1$
$\Leftrightarrow (1-a)[(1-b)(1-c)-\frac{1}{b+c+1}] \leq 0$.
Có $1-a \geq 0\; \forall\; a \in [0;1]$.
Ta sẽ chứng minh $(1-b)(1-c)-\frac{1}{b+c+1}\leq 0$
$\Leftrightarrow (1-b)(1-c)(b+c+1)-1 \leq 0$.
Thật vậy, áp dụng bổ đề trên cho 3 số dương $1-b; 1-c$ và $b+c+1$:
$(1-b)(1-c)(b+c+1)-1\leq \frac{(1-b+1-c+b+c+1)^3}{27}-1=1-1=0$
$\Rightarrow$ đpcm.
Dấu đẳng thức xảy ra $\Leftrightarrow \left\{\begin{matrix}
a=b=c\\
\begin{bmatrix}
1-a=0\\
1-b=1-c=b+c+1
\end{bmatrix}
\end{matrix}\right.$
$\Leftrightarrow a=b=c=0$ hoặc $a=b=c=1$.
Kết luận: Vậy $\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}+(1-a)(1-b)(1-c)\leq 1$ với $a,b,c$ thuộc $[0;1]$. Dấu đẳng thức xảy ra $\Leftrightarrow (a;b;c)=(0;0;0)(1;0;0);(0;1;0);(0;0;1);(1;1;0);(1;0;1);(0;1;1);(1;1;1)$.
=====
Điểm bài làm: 10
Tổng điểm: $S = \left [\frac{52 - \left (6 - 5 \right )}{2} \right ]+3*10+10+0=65$

Vấn đề ở chỗ nào vậy, mình vẫn còn kém nên rất mong bạn chỉ rõ cho . nếu đúng thì..... hình như mấy mở rộng của mình hơi bị trùng lập.....
_____________________________________________________________

Ở mở rộng 1 bạn chia 2 vế cho $b$ khi chưa chắc $b \ne 0$.
Ở các mở rộng tiếp theo thì mình nghĩ bạn nên giải hẳn ra $x$ chứ ko chỉ dừng lại nửa chừng.
Mở rộng 4 và 5 bạn phải xét trường hợp $y$ chẵn hay lẻ.
Mở rộng 5 thì hình như bạn viết sai đề.
Ngoài ra trong quá trình đánh còn có 1 số chỗ sai latex.

Mở rộng của bạn minhhieukaka có vấn đề. Mở rộng của Tru09 hơi giống nhau.

Đề của MSS01 - BlackSelena:
Cho $\triangle XYZ$, $W$ là điểm thuộc cạnh $YZ$. Trên $XY$ và $XZ$ lần lượt lấy các điểm $M$ và $N$. Các đường thẳng qua $M$ và $N$ song song với $XW$ cắt $YZ$ tại $Q$ và $P$. CMR:
$$S_{PMQN} \leq max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}$$

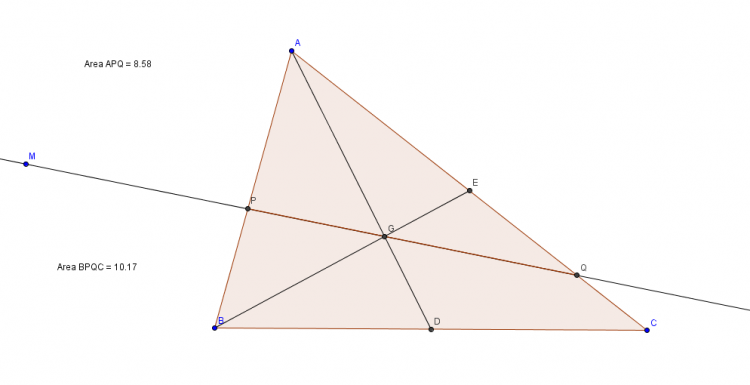
Bổ đề 1: Cho $\triangle{ABC}$; $D,E$ lần lượt nằm trên cạnh $AB,AC$. CMR: $\frac{S_{ADE}}{S_{ABC}}=\frac{AD.AE}{AB.AC}$.

Chứng minh: $\triangle{ADE}$ và $\triangle{AEB}$ có chung đường cao $EH \Rightarrow \frac{S_{ADE}}{S_{AEB}}=\frac{AD}{AB}\; (1)$.
$\triangle{AEB}$ và $\triangle{ABC}$ có chung đường cao $BK \Rightarrow \frac{S_{AEB}}{S_{ABC}}=\frac{AE}{AC}\; (2)$.
Từ $(1),(2) \Rightarrow \frac{S_{ADE}}{S_{ABC}}=\frac{AD.AE}{AB.AC}$.
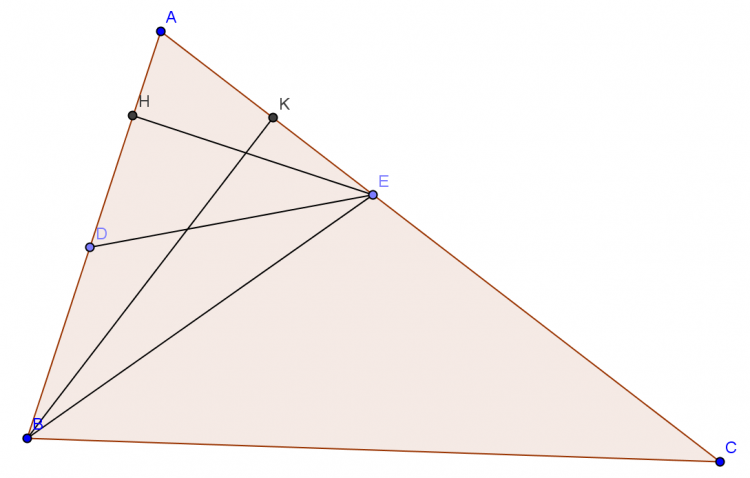
Bổ đề 2: Cho $\triangle{ABC}\sim \triangle{A'B'C'}$. CMR: $\frac{S_{ABC}}{S_{A'B'C'}}=\frac{AB^2}{A'B'^2}$.

Chứng minh: Hạ đường cao $AD, A'D'$.
$\triangle{ABC}\sim \triangle{A'B'C'}\Rightarrow \widehat{ABC}=\widehat{A'B'C'}$ và $\frac{AB}{A'B'}=\frac{BC}{B'C'}\; (1)$
$\Rightarrow \triangle{ABD}\sim \triangle{A'B'D'}\; (g.g)\Rightarrow \frac{AB}{A'B'}=\frac{AD}{A'D'}\; (2)$.
Từ $(1);(2)\Rightarrow \frac{S_{ABC}}{S_{A'B'C'}}=\frac{AD.BC}{A'D'.B'C'}=\frac{AB}{A'B'^2}$.

Quay trở lại bài toán:

Giả sử $max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}=S_{XYW}\Rightarrow S_{XYZ}\leq 2S_{XYW}$.
Đặt $YM=a; ZN=b; XY=x; ZX=y$.
Áp dụng bổ đề 2, ta có: $\frac{S_{YMQ}}{S_{YXW}}=\frac{a^2}{x^2}$ và $\frac{S_{ZNP}}{S_{ZXW}}=\frac{b^2}{y^2}$.
Áp dụng bổ đề 1, ta có: $\frac{S_{XMN}}{S_{XYZ}}=\frac{XM.XN}{XY.XZ}=\frac{(x-a)(y-b)}{xy}=1-\frac{a}{x}-\frac{b}{y}+\frac{ab}{xy}$
$\Rightarrow S_{MNPQ}=S_{XYZ}-S_{YMQ}-S_{ZNP}-S_{XMN}$
$=S_{XYW}+S_{XZW}-\frac{a^2}{x^2}S_{XYW}-\frac{b^2}{y^2}S_{XZW}-(1-\frac{a}{x}-\frac{b}{y}+\frac{ab}{xy})(S_{XYW}+S_{XZW})$
$=(1-\frac{a^2}{x^2}-1+\frac{a}{x}+\frac{b}{y}-\frac{ab}{xy})S_{XYW}+(1-\frac{b^2}{y^2}-1+\frac{a}{x}+\frac{b}{y}-\frac{ab}{xy})S_{XZW}$
$=(\frac{a}{x}+\frac{b}{y}-\frac{a^2}{x^2}-\frac{ax}{by})S_{XYW}+(\frac{a}{x}+\frac{b}{y}-\frac{b^2}{y^2}-\frac{ax}{by})S_{XZW}$
$\le [2(\frac{a}{x}+\frac{b}{y})-\frac{a^2}{x^2}-\frac{b^2}{y^2}-2\frac{ab}{xy}]S_{XYW}$.
Phải c/m: $S_{MNPQ}\le S_{XYW}$
$\Leftrightarrow 2(\frac{a}{x}+\frac{b}{y})-\frac{a^2}{x^2}-\frac{b^2}{y^2}-2\frac{ab}{xy}\le 1$
$\Leftrightarrow (\frac{a}{x}+\frac{b}{y}-1)^2\le 0$.
Bất đẳng thức cuối hiển nhiên đúng.
Dấu đẳng thức xảy ra $\Leftrightarrow \left\{\begin{matrix}
\frac{a}{x}+\frac{b}{y}=1\\
S_{XYW}=S_{XZW}
\end{matrix}\right.$
$\Leftrightarrow \frac{YM}{XY}+\frac{ZN}{XZ}=1$ và $W$ là trung điểm $YZ$.
Kết luận: Vậy $S_{PMQN} \leq max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}$. Dấu đẳng thức xảy ra $\Leftrightarrow \frac{YM}{XY}+\frac{ZN}{XZ}=1$ và $W$ là trung điểm $YZ$.
====
Điểm bài làm: 10
Tổng điểm: $S = \left [\frac{52 - \left (6 - 5 \right )}{2} \right ]+3*10+0+0=55$

Lời giải của toán thủ ConanTM:
Đặt: S(a) = $a^2-a-b^2$. Giả sử S(a) là số chính phương thì S(1-a) cũng là số chính phương mà a và 1 - a khác tính chẵn lẻ => Mâu thuẫn vì theo giả thiết thì a và b phải cùng tính chẵn lẻ. (đpcm)
=================================
Mở rộng 1 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(a+m)^2-(a+m)-b^2$ (với m nguyên dương) không là số chính phương vì nếu S(a+m) là số chính phương thì ta cũng có S[1-(a+m)] cũng là số chính phương mà a + m và 1 - (a + m) khác tính chẵn lẻ => mâu thuẫn.
Mở rộng 2 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(ma)^2-ma-b^2$ (với m nguyên dương) không là số chính phương vì nếu S(am) là số chính phương thì ta cũng có S[1-(am)] cũng là số chính phương mà a m và 1 - (a m) khác tính chẵn lẻ => mâu thuẫn.
Mở rộng 3 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(na+m)^2-(na+m)-b^2$ (với m, n nguyên dương) không là số chính phương vì nếu S(na+m) là số chính phương thì ta cũng có S[1-(na+m)] cũng là số chính phương mà na + m và 1 - (na + m) khác tính chẵn lẻ => mâu thuẫn.
----
Điểm bài làm: 10
Tổng điểm: $\left [ \dfrac{52-\left ( 23-19 \right )}{2} \right ]+3.10+3.10+10=94$

Anh có thể giải thích cách làm của bạn ConanTM được ko ạ?

Lời giải của daovuquang:
Bổ đề 1 (định lí Fermat nhỏ): Nếu $a$ là số tự nhiên và $p$ là số nguyên tố, thì $a^{p-1} \equiv 1 \pmod{p}$. Về cách chứng minh có thể tham khảo tại: http://diendantoanho...ung-bằng-a-mau/
Bổ đề 2: Nếu $p$ là số nguyên tố và $a^2+b^2$ chia hết cho $p$ thì cả $a,b$ đều chia hết cho $p$ với $p \equiv 3 \pmod{4}$
CM:
Giả thiết phản chứng $a,b$ không chia hết cho $p$ suy ra $gcd(a,p)=1$ và tương tự với b
Đặt $p=4k+3$
Xét số $a^{4k+2}+b^{4k+2}$ ta có:
$a^{4k+2}+b^{4k+2}=(a^2)^{2k+1}+(b^2)^{2k+1}=(a^2+b^2)*(…)\; (1)$.
Lại theo đề bài $a^2+b^2$ chia hết cho $p$ suy ra từ $(1)$ ta có $a^{4k+2}+b^{4k+2}$ chia hết cho $p\; (2)$.
Lại theo định lý Fermat nhỏ: $a^{p-1} \equiv 1 \pmod{p}$ và tương tự với $b$
Suy ra $a^{p-1}- b^{p-1}=a^{4k+2}- b^{4k+2}$ chia hết cho $p\; (3)$.
Từ $(2)$ và $(3)$ suy ra $2b^{4k+2}$ chia hết cho $p\Rightarrow b$ chia hết cho $p$. Suy ra $a$ cũng chia hết cho $p$.
Vậy giả thiết phản chứng là sai $\Rightarrow$ bổ đề được chứng minh.

Quay trở về bài toán:
Giả sử $a^2-a-b^2=x^2\; (x \in \mathbb{N})$
$\Leftrightarrow 4a^2-4a-4b^2=4x^2$
$\Leftrightarrow (4a^2-4a+1)-4b^2=4x^2+1$
$\Leftrightarrow (2a-1)^2-(2b)^2=4x^2+1$
$\Leftrightarrow (2a-2b-1)(2a+2b-1)=4x^2+1\; (1)$.
Nhận xét: $2a+2b-1=2(a+b)-1 \equiv -1 \equiv 3 \pmod{4}$
$\Rightarrow 2a+2b-1$ có ít nhất một ước p có dạng $4k+3$.
Từ $(1)\Rightarrow 4x^2+1 \vdots p$. Áp dụng bổ đề trên, ta có $1 \vdots p$ mà $p$ có dạng $4k+3 \Rightarrow$ vô lí.
Vậy $a^2-a-b^2$ không thể là số chính phương.
----
Nhận xét: Mở rộng 1 và 2 của em là thay điều kiện của bài toán đầu (mở rộng 1 là em thêm điều kiện khác vào chỉ mất một dòng còn mở rộng hai thì $a-b$ và $a+b$ cùng tính chẵn lẻ rồi mà?).
----
Điểm bài làm: 10
Tổng điểm: $\left [ \dfrac{52-\left ( 21-19 \right )}{2} \right ]+3.10+0+0=55$